足し算する量子回路をblueqatで作ったので公開したいと思います。
EMANの物理学「量子ゲートで足し算」を参考に作成しました。
理論的なことはとてもわかりやすくこのサイトに書いてあります。
(EMANの物理学には大学生の頃からお世話になっています。本当にありがとうございます。)
上記サイトにある「量子版加算器」を縦に並べたらて任意の桁数の足し算できるよなぁと思ったので、blueqatを用いて書いてみました。
コードは以下になります。
from blueqat import Circuit
class Calculator():
def __init__(self, shots = 1):
self.a = 0
self.b = 0
self.shots = shots
self.initial_state = Circuit()
self.M = 0
def prepare_qubits(self):
#入力a,bを二進数に変換
bin_a = bin(self.a)[2:]
bin_b = bin(self.b)[2:]
#bin_a,bin_bのqubit列の最大の長さをLとする
L = max(len(bin_a), len(bin_b))
#bin_a,bin_bのqubit列の最小の長さをlとする
l = min(len(bin_a), len(bin_b))
#qubit列を長い方に合わせる
if len(bin_a) > len(bin_b):
bin_b = "0" * (L-l) + bin_b
else:
bin_a = "0" * (L-l) + bin_a
#入力の(0,1)を準備
initial_qubits = "0"
for a, b in zip(reversed(bin_a), reversed(bin_b)):
initial_qubits = initial_qubits + a + b + "0"
# qubit全体の長さをMとする
self.M = len(initial_qubits)
#initial stateを準備する
initial_state = Circuit(len(initial_qubits))
cnt = 0
for q in initial_qubits:
if q == "1":
initial_state += Circuit().x[cnt]
cnt += 1
self.initial_state = initial_state
return initial_state
def query(self, i):
# EMANの物理学「量子ゲートで足し算」に登場する量子版加算器一つ分の演算
return Circuit().toffoli[1+i,2+i,3+i].cx[1+i,2+i].toffoli[0+i,2+i,3+i].cx[0+i,2+i]
def adder(self, a, b):
self.a = a
self.b = b
self.prepare_qubits()
state = self.initial_state
#量子回路で足し算を実行
for i in range(self.M):
if i % 3 == 0:
state = state + self.query(i)
#量子回路を測定する
final_state = state.m[:].run(shots = self.shots)
final_state = list(final_state.keys())[0]
#足し算の結果のqubitに対応する部分のみ抜き出す入れ物を作る
result_binary = ""
#足し算の結果のqubitに対応する部分のみ抜き出す
cnt = 0
for q in final_state:
if (cnt + 1) % 3 == 0:
result_binary = q + result_binary
cnt += 1
#二進数を10進数に直す
result = int(result_binary, 2)
return result
計算するには以下の様にしてやれば良いです。
cal = Calculator() #インスタンス作成
cal.adder(2,4) #2+4の足し算を実行
コードの解説 (2020/10/8 追記
簡単にコードの説明をしたいと思います。
このCalculatorクラスは大きく分けて「prepare_qubits」と「adder」の二つのメゾットから成り立ちます。
prepare_qubits
prepare_qubitsメゾットでは、初期状態のqubitを準備します。まずどの様な初期状態を準備するのかというところから見ていきたいと思います。
そもそも作りたいものはEMANの物理学「量子ゲートで足し算」に登場する量子版加算器(以後足し算器と呼びます)を縦に並べたものです。回路は具体的な計算を考えた方が分かりやすいと思うので、$a+b=c$の足し算を考えてみたいと思います。ここで、$a$の二進数表記を$a_4a_3a_2a_1$、$b$の二進数表記を$b_4b_3b_2b_1$としてこれらを入力とします。そうすれば回路は以下の様になります。
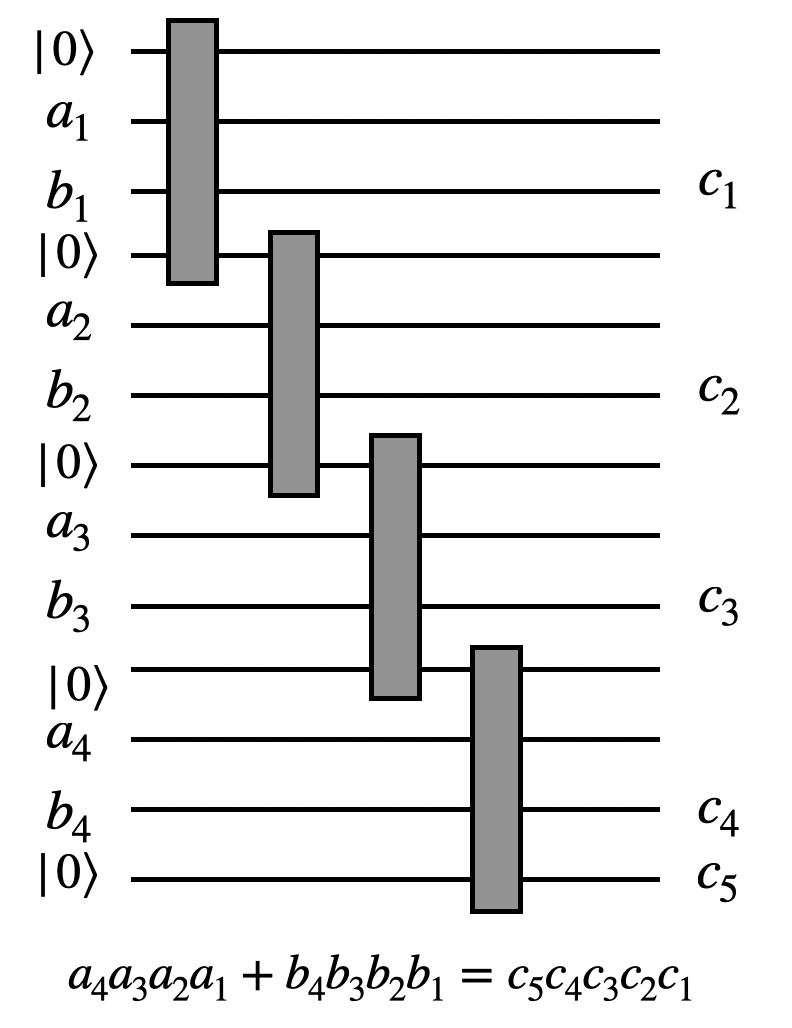
ここで$c_5c_4c_3c_2c_1$は$c$の二進数表記であり、グレーの四角は以下の様に足し算器を表しています。
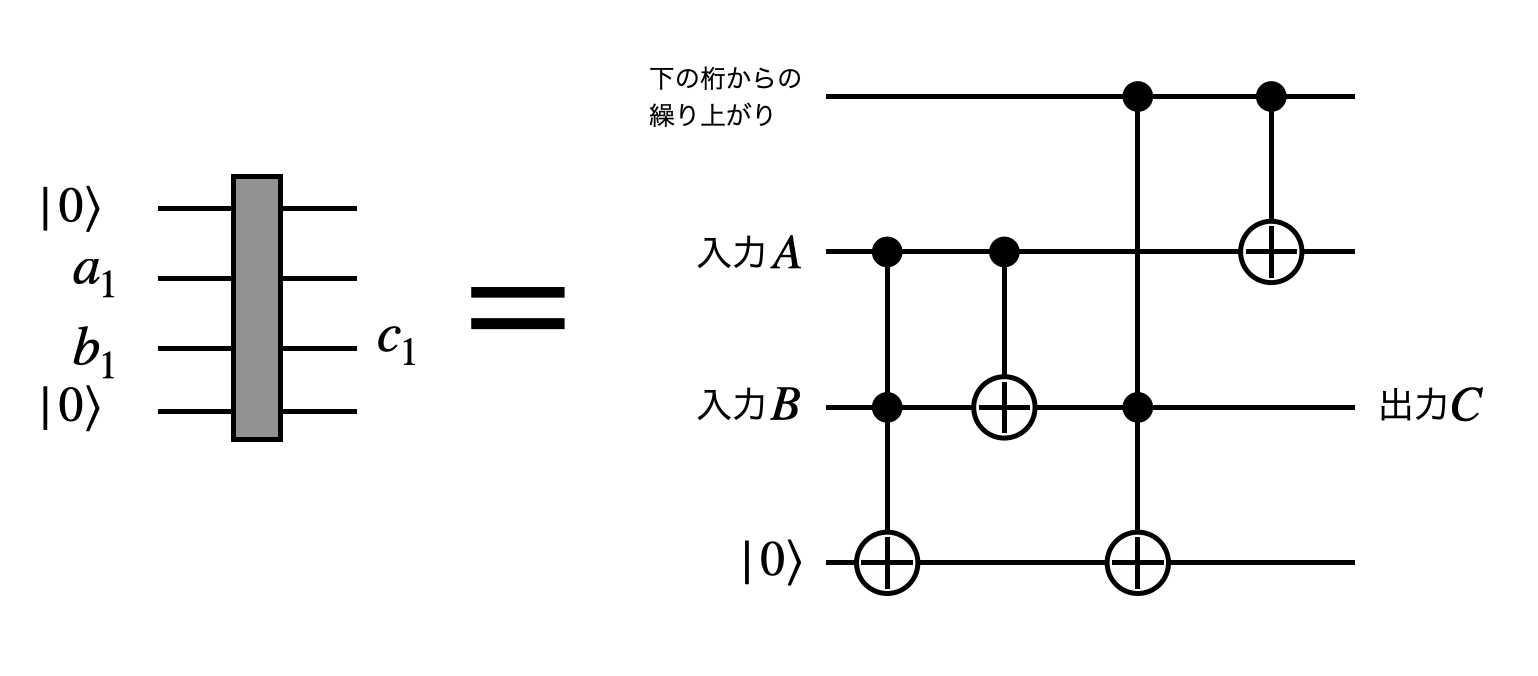
この様にして足し算ができるわけです。つまり欲しい初期状態は
$$|0a_1b_10a_2b_20a_3b_30a_4b_40\rangle$$
といったものになります。この状態をprepare_qubitsメゾットで準備しています。具体的に以下の様な手順で準備しました。
- まずは入力を二進数に変換します。
- 変換した入力の桁数を桁数の多い方に合わせます。(桁数を合わせなければならないのは図をみていただければわかると思います。)
- 文字列$0a_1b_10a_2b_20a_3b_30a_4b_40$を作ります。
- 文字列の長さ分だけ$|0\rangle$を準備します。
- 準備した$|0000000000000\rangle$にXゲートを演算させて$|0a_1b_10a_2b_20a_3b_30a_4b_40\rangle$を作ります。
欲しい状態が手に入りました。あとは足し算器を演算させていくだけです。
adder
足し算器を演算させて足し算した結果を取り出すメゾットになります。以下の様な構成になってます。
- 初期状態を手に入れるためにprepare_qubitsを実行します。
- 足し算器を演算させます。(ここで足し算器はqueryというメゾットにまとめました。)
- 量子回路を測定します。
- 足し算した結果を取り出します。
- 取り出した結果を十進数に変換します。
以上で足し算ができました。
以上、初投稿でした。この様な感じで良いのでしょうか。。。