フリーで使えるエクセル統計ツールの出力結果が間違っているかもしれないという話（コレスポンデンス分析について）

1.はじめに

最近、職場のN氏からコレスポンデンス分析に関することでコメントを求められ、色々と試行錯誤した。その際、後述するエクセルの統計アドインツールの結果が、SASやRなどの統計パッケージの結果と一致しないことに気がついた。

2.問題の所在

まずは数字を適当に入力したデータテーブルを作って、SASのcorrespプロシジャを試してみる。

proc sql;
  create table df
  (brands CHAR(5) NOT NULL,
   attr1 float NOT NULL,
   attr2 float NOT NULL,
   attr3 float NOT NULL,
   attr4 float NOT NULL,
   attr5 float NOT NULL,
   attr6 float NOT NULL,
   attr7 float NOT NULL,
   constraint prim_key
   primary key (brands)
  );

  insert into df values ("A社", 4.72, 4.94, 5.26, 4.89, 4.97, 4.93, 4.94);
  insert into df values ("B社", 4.55, 4.31, 5.06, 4.60, 4.85, 4.53, 4.59);
  insert into df values ("C社", 4.72, 4.26, 5.23, 4.59, 5.02, 5.08, 4.60);
  insert into df values ("D社", 4.63, 4.69, 5.18, 4.96, 4.92, 4.91, 4.72);
  insert into df values ("E社", 4.52, 4.66, 5.31, 4.91, 4.91, 5.18, 4.88);
  insert into df values ("F社", 5.12, 5.54, 5.80, 5.43, 5.43, 5.63, 5.48);
  insert into df values ("G社", 4.58, 4.58, 5.38, 5.02, 5.08, 5.33, 4.93);
  insert into df values ("H社", 4.56, 4.46, 4.95, 4.73, 4.86, 4.69, 4.55);
  insert into df values ("I社", 4.69, 4.75, 5.17, 4.92, 5.10, 4.91, 4.91);
  insert into df values ("J社", 4.55, 4.52, 5.44, 4.95, 5.04, 5.52, 5.00);
  insert into df values ("K社", 4.60, 4.35, 5.16, 4.68, 4.90, 4.79, 4.68);
  insert into df values ("L社", 5.13, 5.33, 5.69, 5.41, 5.31, 5.60, 5.10);
  insert into df values ("M社", 4.66, 4.68, 5.31, 4.88, 5.12, 5.24, 4.92);
  insert into df values ("N社", 4.91, 5.17, 5.57, 5.21, 5.27, 5.30, 5.04);
  insert into df values ("O社", 4.66, 4.69, 5.36, 4.95, 5.06, 5.23, 4.92);
quit;

data df; set df;
  label attr1="顧客重視" attr2="革新的" attr3="信頼できる" attr4="積極的" attr5="親しみやすい"  attr6="財務的に安定"  attr7="評判が良い";
run;

proc corresp data=DF;
  var attr1 - attr7;
  id brands;
run;

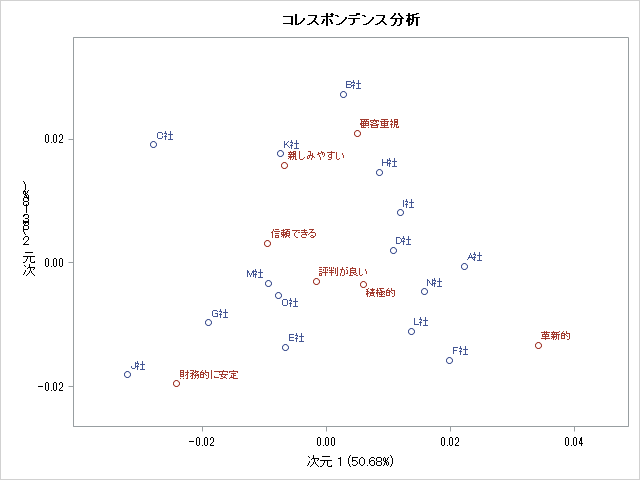
これと同じことを例のエクセル統計アドインツールを使って試す。エクセルのシート上の対象範囲のデータを選択するだけで、以下のようなプロットを自動で出力してくれる。

２つの結果を見比べてみると次のような相違点がある。

1. X軸とY軸のスケールが異なる
2. 青くプロットされた点だけがY軸を対称に左右反転している

1つ目のポイントは分析結果の解釈に影響を及ぼさないので、脚注のコメントだけに留めておく¹。2つ目のポイントは重大であり、コレスポンデンス分析の結果から全くでたらめな示唆や解釈を導くという深刻な事態を招いてしまう。
それでは、このプロットから正しい示唆を読み取るには、どうすればいいか。

最近は何事も統計パッケージを使って簡単に分析できるようになった。なんにせよ、その背後の仕組みを理解しないまま盲目的に統計ツールを使用するのは、あまり良いことではない。そこで本稿では

• コレスポンデンス分析の手順
• 結果の解釈の仕方

について述べる。

3.コレスポンデンス分析の手順

Qualtrics の Jeffrey Hao氏（リンク）の解説が分かりやすい。以下に要旨をまとめる。

ステップ１

• 分析対象となるデータテーブルを用意する²。例のエクセルのアドインツールを使う場合は、このデータの対象範囲を選択してボタンを押すだけでOK。
• 以下の合計をそれぞれ算出しておく。
  • 行の合計
  • 列の合計
  • 総合計

ステップ２

• 出現割合を求める。各セルの数値を総合計で割ればよい。このテーブルをPと呼ぶことにする。

ステップ３

• 出現割合の「理論値」を計算する。ステップ2で求めた「行の割合合計」と「列の割合合計」の数値をかけ合わせればOK。このテーブルをEと呼ぶことにする。
• このテーブルEは「表頭と表側との間に関係性が全くなく、両者の出来事は独立して起きる」という仮定の下で期待される出現割合を表している³。

ステップ４

• 理論値（E）からの出現割合（P）のズレを計算する。PからEを引けばよい。このテーブルをRと呼ぶことにする。

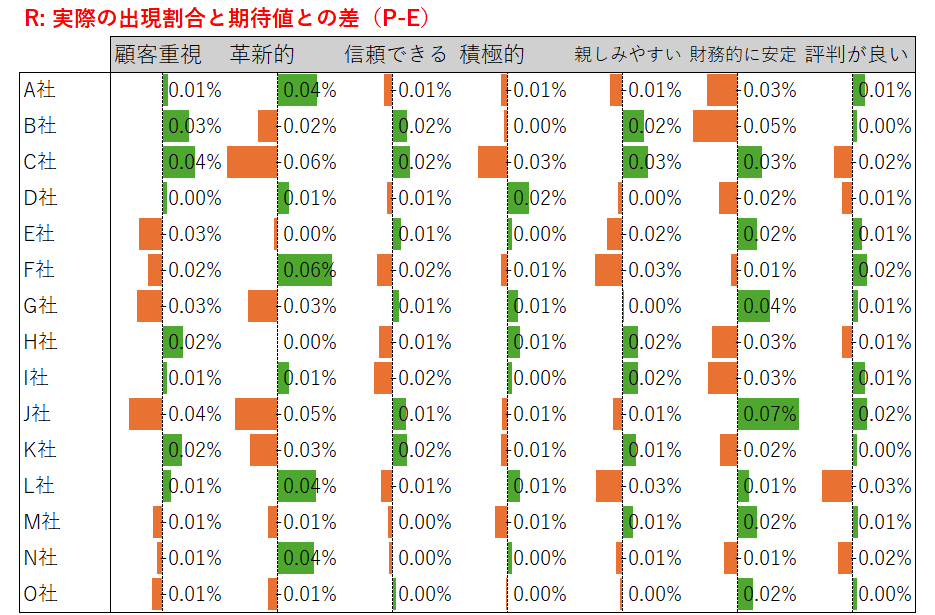
ステップ５

• テーブルRに対して特異値分解を行う。左側行列U、特異値行列S、右側行列V（転置）をそれぞれ得る。

R = USV^T

• 結果を可視化する。 左側行列U（右側行列V）の第1列（行）および第2列（行）を、それぞれ第1主軸と第2主軸に転写して散布図を取る。

補足

実を言うと、ステップ5の説明は正しくない。正確に書くと、テーブルRに対して特異値分解を行うのではなく、実際には以下のようにスケールの調整を行っている。

• RをEの平方根で割った行列に対して特異値分解を行う
• 左側行列Uの各列を列の割合合計の平方根で割る
• 右側行列Vの各行を行の割合合計の平方根で割る
• 左側行列U（右側行列V）の第1列（行）および第2列（行）に対して、第1特異値と第2特異値をそれぞれ乗じる

…が、この部分はあまり本質的な点ではない。コレスポンデンス分析のエッセンスは、上記のステップから分かるように、「実際の出現割合Pが理論値Eからどの程度ズレているか」を特異値分解によって抽出し、可視化することにある。

実装

上記のステップをPythonで実装してみよう。mcaなどコレスポンデンス分析の専用モジュールを使わずに、numpyモジュールのlinalg.svdメソッドを使って特異値分解を行う。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib

data = [
    [4.72, 4.94, 5.26, 4.89, 4.97, 4.93, 4.94],
    [4.55, 4.31, 5.06, 4.60, 4.85, 4.53, 4.59],
    [4.72, 4.26, 5.23, 4.59, 5.02, 5.08, 4.60],
    [4.63, 4.69, 5.18, 4.96, 4.92, 4.91, 4.72],
    [4.52, 4.66, 5.31, 4.91, 4.91, 5.18, 4.88],
    [5.12, 5.54, 5.80, 5.43, 5.43, 5.63, 5.48],
    [4.58, 4.58, 5.38, 5.02, 5.08, 5.33, 4.93],
    [4.56, 4.46, 4.95, 4.73, 4.86, 4.69, 4.55],
    [4.69, 4.75, 5.17, 4.92, 5.10, 4.91, 4.91],
    [4.55, 4.52, 5.44, 4.95, 5.04, 5.52, 5.00],
    [4.60, 4.35, 5.16, 4.68, 4.90, 4.79, 4.68],
    [5.13, 5.33, 5.69, 5.41, 5.31, 5.60, 5.10],
    [4.66, 4.68, 5.31, 4.88, 5.12, 5.24, 4.92],
    [4.91, 5.17, 5.57, 5.21, 5.27, 5.30, 5.04],
    [4.66, 4.69, 5.36, 4.95, 5.06, 5.23, 4.92],
]
brands = ["A社", "B社",	"C社",	"D社",	"E社",	"F社",	"G社",	"H社",	"I社",	"J社",	"K社",	"L社",	"M社",	"N社", "O社",]
attributes = ["顧客重視", "革新的", "信頼できる", "積極的", "親しみやすい", "財務的に安定", "評判が良い"]
df = pd.DataFrame(data, index=brands, columns=attributes)
print("元データ：", df,'\n')

# Observed Proportions
total = df.values.sum()
P = df/total
print("出現割合：", P,'\n')

# Row and Column Masses
rowsum = P.sum(axis=0)
colsum = P.sum(axis=1)
print("行の割合の合計：", rowsum,'\n')
print("列の割合の合計：", colsum,'\n')

# Expected Proportions
E = pd.DataFrame(np.outer(colsum, rowsum), index=brands, columns=attributes)
print("期待値：", E,'\n')

# Residuals
R = P - E
print("期待値からの残差：", R,'\n')

# Standardized Residual
Z = R / np.sqrt(E)
print("標準化された残差：", Z,'\n')

# Sigular Value Decomposition
U, S, V = np.linalg.svd(Z, full_matrices=True)
U = pd.DataFrame(U, index=brands, columns=brands)
V = pd.DataFrame(V, index=attributes, columns=attributes)
singular1 = np.diag(S)[0,0]
singular2 = np.diag(S)[1,1]

# Variance Expressed by the Dimensions
print("第1主成分値（固有値）:", np.diag(S)[0,0]**2, '\n')
print("第2主成分値（固有値）:", np.diag(S)[1,1]**2, '\n')

print("第1主成分の寄与度：", format(S[0]**2/sum(S**2), ".2%"))
print("第2主成分の寄与度：", format(S[1]**2/sum(S**2), ".2%"))

# Standard Coordinates
brand_std_coord = pd.DataFrame(
                  [U.iloc[:,col]/np.sqrt(colsum) for col in range(U.shape[1])]
                  ,index=brands).T
attr_std_coord =  pd.DataFrame(
                  [V.iloc[row,:]/np.sqrt(rowsum)  for row in range(V.shape[0])]
                  ,index=attributes)

# Plot
plt.scatter(singular1 * brand_std_coord.iloc[:, 0], 
            singular2 * brand_std_coord.iloc[:, 1], 
            c='blue', label='Brands') 
plt.scatter(singular1 * attr_std_coord.iloc[0, :], 
            singular2 * attr_std_coord.iloc[1, :], 
            c='red', label='Attributes')

for i, txt in enumerate(brands):
    plt.annotate(txt, (singular1 * brand_std_coord.iloc[i, 0], singular2 * brand_std_coord.iloc[i, 1]))
for i, txt in enumerate(attributes):
    plt.annotate(txt, (singular1 * attr_std_coord.iloc[0, i], singular2 * attr_std_coord.iloc[1, i]))

plt.legend()
plt.grid(linewidth=0.2)
plt.xlabel(f'Dimension 1 ({S[0]**2/sum(S**2):.2%})')
plt.ylabel(f'Dimension 2 ({S[1]**2/sum(S**2):.2%})')
plt.title('Correspondence Analysis')
plt.show()

先の出力結果と比べてみると、列の属性とブランド属性が同じ方向を向いていることから、SASのアウトプットと同じ結果が得られていることがわかる。
念のため、Rのcaパッケージで同じ結果が得られるか確かめてみよう。

library(tidyverse)
library(ca)

data <- matrix(c(
  4.72, 4.94, 5.26, 4.89, 4.97, 4.93, 4.94,
  4.55, 4.31, 5.06, 4.60, 4.85, 4.53, 4.59,
  4.72, 4.26, 5.23, 4.59, 5.02, 5.08, 4.60,
  4.63, 4.69, 5.18, 4.96, 4.92, 4.91, 4.72,
  4.52, 4.66, 5.31, 4.91, 4.91, 5.18, 4.88,
  5.12, 5.54, 5.80, 5.43, 5.43, 5.63, 5.48,
  4.58, 4.58, 5.38, 5.02, 5.08, 5.33, 4.93,
  4.56, 4.46, 4.95, 4.73, 4.86, 4.69, 4.55,
  4.69, 4.75, 5.17, 4.92, 5.10, 4.91, 4.91,
  4.55, 4.52, 5.44, 4.95, 5.04, 5.52, 5.00,
  4.60, 4.35, 5.16, 4.68, 4.90, 4.79, 4.68,
  5.13, 5.33, 5.69, 5.41, 5.31, 5.60, 5.10,
  4.66, 4.68, 5.31, 4.88, 5.12, 5.24, 4.92,
  4.91, 5.17, 5.57, 5.21, 5.27, 5.30, 5.04,
  4.66, 4.69, 5.36, 4.95, 5.06, 5.23, 4.92
), nrow = 15, byrow = TRUE)

brands <- c("A社", "B社", "C社", "D社", "E社", "F社", "G社", "H社", "I社", "J社", "K社", "L社", "M社", "N社", "O社")
attributes <- c("顧客重視", "革新的", "信頼できる", "積極的", "親しみやすい", "財務的に安定", "評判が良い")

df <- as.data.frame(data)
rownames(df) <- brands
colnames(df) <- attributes

res.ca <- ca(df, graph=T)
plot(res.ca)

Pythonでプロットした結果と確かに一致している。

4.コレスポンデンス分析の結果の解釈

DisplayR の Tim Bock氏の記事（リンク）にまとめられている10のポイントが分かりやすい。これらに沿って、先のコレスポンデンス分析の結果を解釈してみよう。括弧は拙訳。

1. Check conclusions using the raw data（コレスポンデンス分析から得られる示唆を、元データを使ってチェックすること）

コレスポンデンス分析のステップを理解していれば、解釈を間違える可能性は低い。
ここでは、可視化した結果を先のテーブルRと見比べてみる。

2. The further things are from the origin, the more discriminating they are （原点からの距離が遠いものほど、際立った特徴を示唆する）

• テーブルRを見ると、「革新的」や「財務的に安定」の列は数値のメリハリが大きい。
• プロットに目を転じると、確かに、この２つの属性は原点から遠く離れている。

3.The closer things are to origin, the less distinct they probably are （原点からの距離が近いものは、おそらく特徴的ではない）

• テーブルRを見ると、「信頼できる」や「評判が良い」の列は数値のメリハリが小さい。
• プロットを見ると、確かに、この２つの属性は原点のすぐ近くにある。

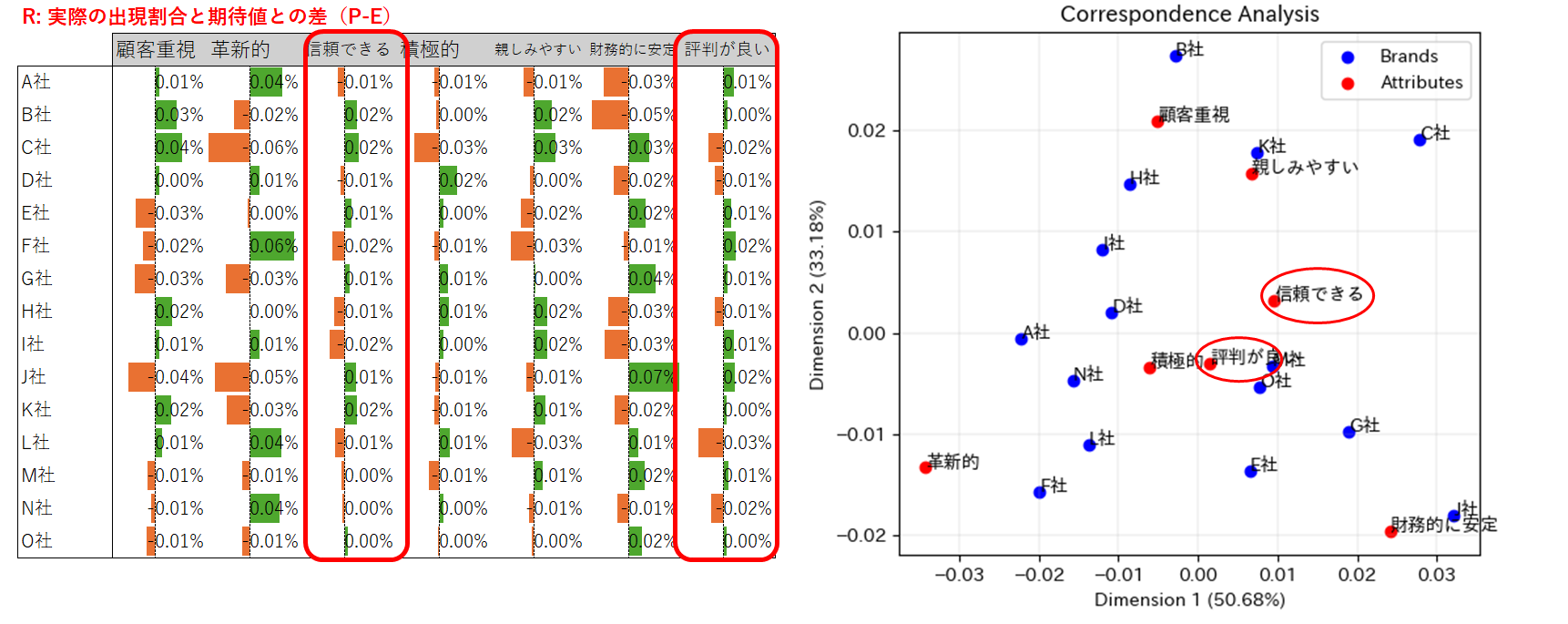
4.The more variance explained, the fewer insights will be missed （説明される分散が大きいほど、コレスポンデンス分析で失われる知見は少ない）

第1軸の寄与度は50.7％、第2軸の寄与度は33.2％を示している。
おおまかにいえば、コレスポンデンス分析の結果は元データの83.9%の情報を保持しているということであり、解釈にあたって支障はなさそうだ。

5. Proximity between row labels probably indicates similarity (if properly normalized) （尺度を適切に取れば、行ラベル同士の距離の近さは類似性を示唆する）

• テーブルRを見ると、A社・F社・L社・N社はいずれも「革新的」の項目で目を引く。それ以外の項目についても、おおむね類似しているように見える。
• プロットを見ると、A社・F社・L社・N社はいずれも「革新的」の周辺に集まっている。

6. Proximity between column labels indicates similarity (if properly normalized)（尺度を適切に取れば、列ラベル同士の距離の近さは類似性を示唆する）

• テーブルRの「顧客重視」「親しみやすい」の2列を見ると、概ね一方がプラス（マイナス）ならば他方もプラス（マイナス）という傾向があり、正の相関がありそうだ。逆に、「革新的」「財務的に安定」の2つの属性には負の相関関係があるように見える。
• プロットを見ると、確かに、「顧客重視」「親しみやすい」の２つの属性は近くにある。逆に「革新的」「財務的に安定」の2つの点は遠く離れている。

7. If there is a small angle connecting a row and column label to the origin, they are probably associated （原点に対して行ラベルと列ラベルのなす角度が小さいほど、両者は関連性を持つ可能性が高い）

• テーブルRから、「財務的に安定」しているのはG社・J社であり、「革新的」なブランドはF社・N社である。
• プロットを見ると、確かに、これらの属性とブランドは同じ方向を向いている。

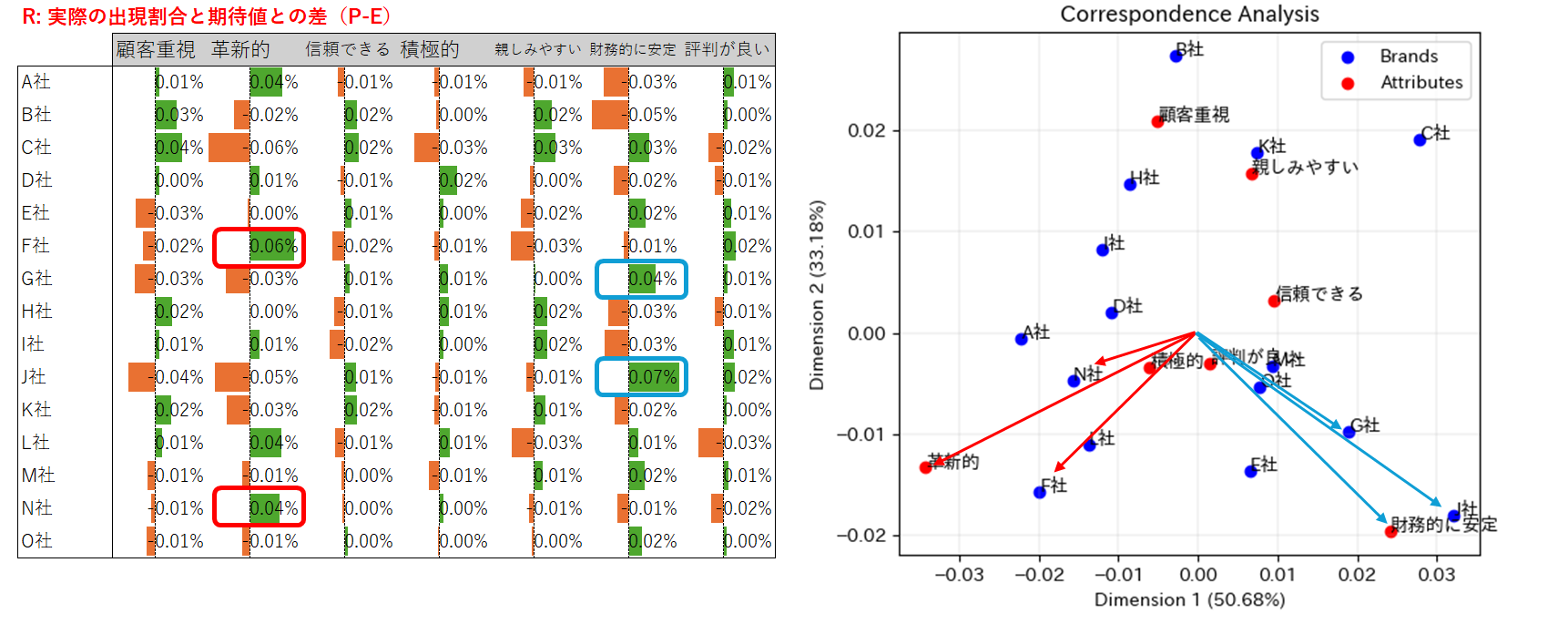
8. A row and column label are probably not associated if their angle to the origin is 90 degrees （原点に対して行ラベルと列ラベルのなす角度が直角の場合、両者の間にはおそらく関連性がない）

• テーブルRから、E社の「革新的」の数値、G社の「親しみやすさ」の数値はいずれもゼロに近い。
• プロットを見ると、確かに、これらの属性とブランドはおおむね原点に対して90度をなしている。

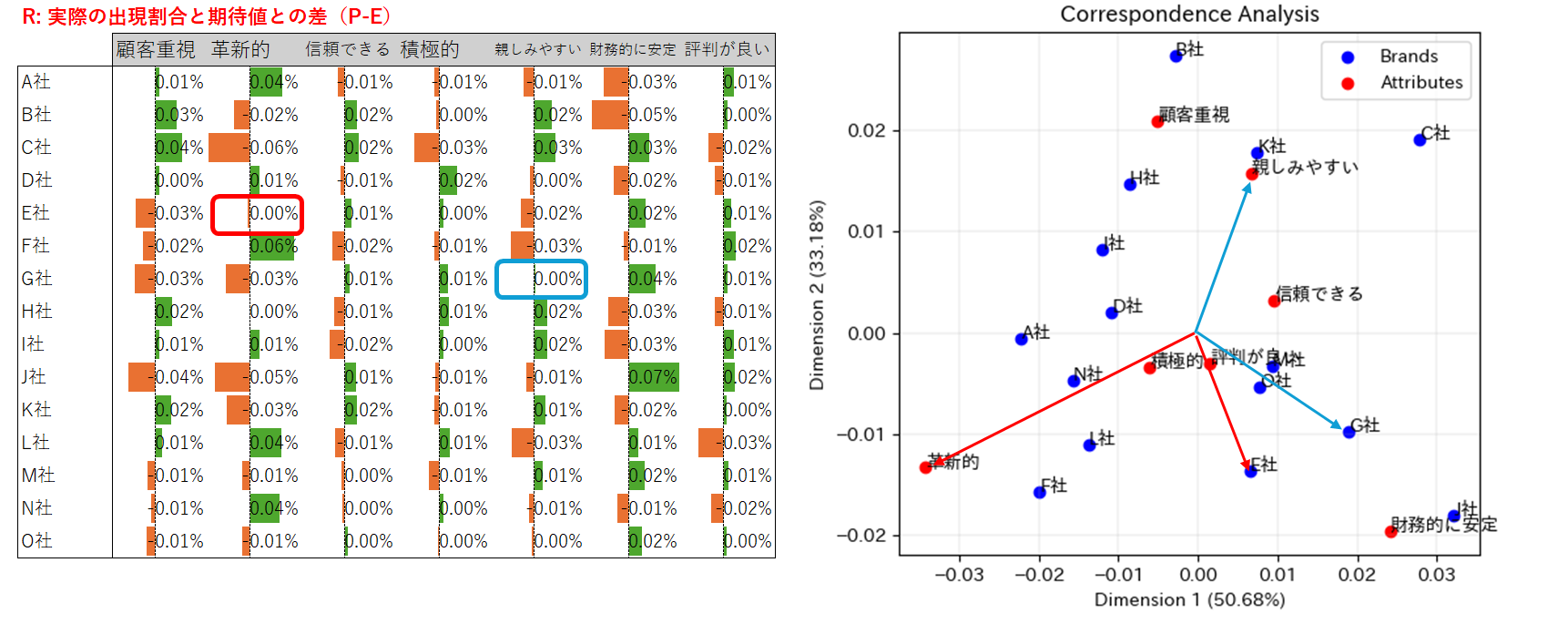
9. A row and column label are probably negatively associated if they are on opposite sides of the origin （原点に対して行ラベルと列ラベルが真逆の位置にある場合、おそらく負の関連性がある）

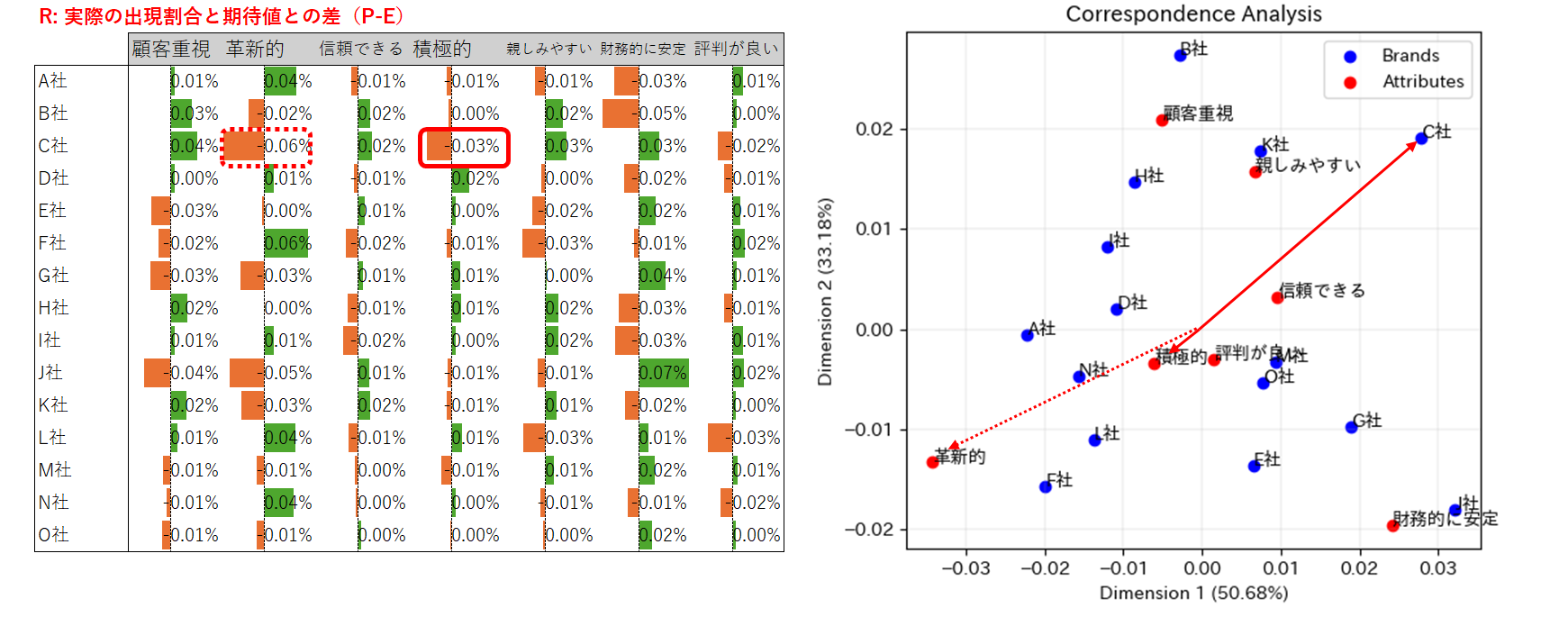
• テーブルRを見ると、C社は「革新的」の項目で大きくマイナスとなっている。
• プロットを見ると、確かに、これらは散布図上で逆方向に位置している。

10. The further a point from the origin, the stronger their positive or negative association （原点から遠く離れているほど、正または負の方向に強い関連性がある）

• テーブルRを見ると、C社は「積極的」の項目でもマイナスとなっているが、「革新的」の項目ほどではない。
• プロットを見ると、C社と「積極的」は逆方向に位置しているが、確かに、その距離は「革新的」との距離ほどではない。

おわりに

まとめると、

• コレスポンデンス分析は「行の項目と列の項目との間にまったく関係がない」場合と比べて、「どの項目の出現頻度が相対的に多いか・少ないか」を可視化するアプローチといえる。
• 可視化に際して表頭または表側の一方が反転してしまうと、全く異なる示唆や結論を導いてしまう。

機能について問い合わせるためにエクセル統計アドインツールの開発元のメディアチャネル社に今年8月中旬にコンタクトしたが、残念ながら現時点で回答を得られていない。

https://media-ch.com/

ウェブサイトにアクセスすると、最終改定履歴が2023年10月7日となっており、このタイミングでコレスポンデンス分析の機能が加わっている。リリースからまだ1年も経っていない（本日2024年9月20日時点）。

なお、

配布において、セキュリティ対策など必要な処理は行なっておりますが、本ソフトウェアを使用した上で、生じたトラブルやいかなる損害に対しても、作者は一切責任を負いませんのでご了承ください。

とのことである。
もしかしたら、近いうちに改訂版がリリースされるか、特にアナウンス等なく、ひっそりと更新されているのかもしれない。もし機能が変わっていることに気がついたら、どなたか教えて下さい。

1. 本稿の「補足」で「左側行列U（右側行列V）の第1列（行）および第2列（行）に対して、第1特異値と第2特異値をそれぞれ乗じる」と書いた。このプロセスをスキップすると、各散布点のポジションは変化せず、X軸とY軸のスケールだけが変化することを確かめられる。 ↩

2. ここでは、各列（属性）は1から7までの範囲をとり、各セルの数値は行（ブランド）ごとの平均点と考えている。コレスポンデンス分析では度数分布（カウントデータ）を使用することが多いそうだが、本稿では問題としない。 ↩

3. 出現割合を確率とみなせば、次が成り立つことと同じ。２つの事象AとBが独立 ⇔ [AかつBが起こる]確率=[Aが起こる]確率×[Bが起こる]確率。 ↩