Go to Qiita Advent Calendar 2024 Top
LoginSignup
40
31

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@s_yaginuma(Shinya Yaginuma)

ロジスティック回帰について調べ、モデルを進化させてみた

Posted at

##はじめに
こんにちは、教育業界に就職した新米データサイエンティストです。
入社してから1ヶ月が経過しようとしています。
先日、Kaggleのタイタニックデータを分析したという記事を書きました。

新米データサイエンティストが覚えたての知識を使ってKaggleのタイタニックデータを分析し、投稿してみた！

こちらの記事で参考にさせて頂いている、KaggleのCTOが教えてくれた”AIエンジニアに超オススメな8つの学習ステップ”によると、機械学習を学ぶ8つのステップは、

  1. あなたが興味を持っているデータ分析の問題を選ぶ
  1. その問題を、Quick & Dirtyに、ハックして、最初から最後まで一貫して解決する
  2. 自分の作った学習モデルを進化させて改善する
  3. 自分のソリューションを共有する
  4. さまざまな問題のセットで＃1-4を繰り返す
  5. Kaggleのコンペに真剣に挑戦する
  6. 専門レベルを上げて機械学習を適用する
  7. 機械学習を他の人に教える

であり、前回の記事で2までをやりました。
次に3のステップに進むにあたり、グリッドサーチや交差検証を用いて最適なモデルを探していこうと考えています。
しかし、自分は肝心のアルゴリズム自体の理解をまだしていません（笑）

そこで、今回ロジスティック回帰について調べ、モデルを進化させる段階に踏み込んでいこうと思います。
なお、認識の間違いなどあればどしどしご指摘頂けるとありがたいです :bow_tone1: :bow_tone1: :bow_tone1:

※ 自分はロジスティック回帰というと２クラス分類のイメージが強かったのですが、調べていく中で、多クラスの分類にも用いることができると知りました。しかし、当記事では扱うデータが２クラス分類ということで、その領域についてのみ触れさせて頂きます。

##ロジスティック回帰ってなんだ？

次式で表される「ロジスティック関数により、目的変数と説明変数の関係を表現するモデル」です。

y = \frac{1}{1 + exp(-z)}

z = {\beta}_1+{\beta}_2x_1+{\beta}_3x_2…

$z$の中身が線形回帰のようになっていますね。$x_i$が説明変数、${\beta}_1$が切片、${\beta}_2,{\beta}_3,...$がそれぞれの説明変数の係数です。
では$y$が目的変数か、というと違っていて、これはクラスiに属する確率を表しています。

式を見ると、ロジスティック関数は0から1の連続的な値を取ることがわかります。
確率も最小値が0, 最大値が1であり、その間の連続的な値を取ることから、このロジスティック関数が確率を表すのに都合が良いと言うのはなんとなく感じ取れました。

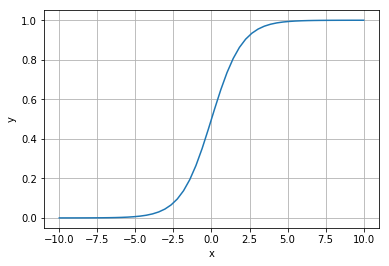
ここで、最も単純な $y = \frac{1}{1 + exp(-x)}$ を図示してみます。

image.png

$x$に関して単調に増加し、$x=0$で0.5を取るといったことがわかります。

では、そのパラメータ${\beta}_1, {\beta}_2,...$はどのように決められているのでしょうか？
それは、次式で表される、「交差エントロピー型誤差関数」を最小にするパラメータを得ることで決定されるようです。
今まで騙し騙し耐えてきましたが、この部分で挫折しそうです。ここでは式を記述するに留めます。

L({\bf w}) = -{\sum_{i=1}^{N}}(t_i{\bf w^Tx_i} - ln(1+exp({\bf w^Tx_i}))

これを${\bf w}$に関して微分し、最急効果法やニュートン法という方法によってパラメータを求めるみたいです。難しい...

以上まとめると、

  • ロジスティック回帰とは、説明変数の線形結合をロジスティック関数に入れ込むことで特定のクラスに属する確率を出力するモデル
  • パラメータは、交差エントロピー型誤差関数を最小化するパラメータに決定される
  • 解析的に求めることは不可能なので、最急降下法やニュートン法などにより数値的に求める

となります！！
全く数式を理解していませんが、この概念さえわかっておけば一旦進める気がします。
次に、scikit-learnのLogisticRegressionについて見ていきます。

##scikit-learnのLogisticRegressionのパラメータたち
http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’, verbose=0, warm_start=False, n_jobs=1)

主要なものを見ていきます。
###・penalty : str, ‘l1’ or ‘l2’, default: ‘l2’
正則化の仕方を決めるパラメータです。
正則化とは、過学習に陥らないよう、モデルが複雑になりすぎないようにペナルティをかける方法のようです。
僕の理解ではまだまだ説明できないので、詳しくはこちらをご参照ください

過学習を防ぐ正則化

###・tol： float, default: 1e-4
本家サイトをgoogle翻訳すると、「基準を停止するための許容差」。
先ほどの誤差関数の値のことでしょうか？

###・C : float, default: 1.0
正則化の強度のようです。値が小さいほど強い正則化（複雑なモデルになりづらくなる）が行われます。

###・class_weight : dict or ‘balanced’, default: None
クラスに重みをつけることができるようです。デフォルトでは1が指定されています。
balancedを指定すると、n_samples / (n_classes * np.bincount(y))の計算式に従い、重みつけがされます。
偏りのあるデータセットに対して予測を行う際に有用そうです。

###・solver : {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}
最適なパラメータの探索方法を設定するようです。先ほどの誤差関数を最小化するパラメータを求める方法のことです。

###・warm_start : bool, default: False
Trueに指定すると、再学習する際にモデルを初期化せず、既に学習したモデルに更に学習を追加することができます。

さて、では次の記事では実際に前回のロジスティック回帰モデルを改良して見ます。

##ロジスティック回帰モデルの改良!!
前回の不十分だった点を列挙してみます。

  • 同じチケット番号の人がいるのか確認、それが同乗者なのか確認
  • Age、Embarkedの欠損値の処理（前回はdropnaで全て落とした）
  • Cabinの中身をみていない
  • 学習用データを更に分割せず、汎化性能を検証していない
  • モデルのパラメータは全てデフォルトのまま

今回は

  • 同乗者がいるのかどうかフラグつけ
  • GridSearchCVを使ってパラメータの最適化と交差検証を行う
    ところまでやってみようと思います。

試しに、同じチケット番号の人のデータをみてみます。

#今回はデータをみやすくするため、訓練データとテストデータを結合してやってみる
merge_data = pd.concat([train_data, test_data], axis=0)
merge_data[merge_data.Ticket == '4133']
スクリーンショット 2018-04-30 11.36.39.png

この場合、家族で乗っているらしいということが見えました！やはり同じチケット番号の人は同乗者と捉えて良さそうです。
その人が生き残るのは同乗者の有無というより、同乗者が生き残っているのかどうかというところに依存しそうですが、ここではParch, SibSpより家族の有無、同じTicketの人がいるかどうかにより、同乗者の有無のフラグ付けをしてみます。

merge_data['have_family'] = (merge_data['Parch'] + merge_data['SibSp']).map(lambda x:1 if x >= 1 else 0)

ticket_counts = merge_data.Ticket.value_counts().reset_index()
ticket_counts.columns = ['Ticket', 'ticket_counts']
merge_data['is_alone'] = pd.merge(merge_data, ticket_counts, how='left', on='Ticket')['ticket_counts'].map(lambda x:0 if x > 1 else 1)
スクリーンショット 2018-04-30 12.05.42.png

うまくフラグ処理できています。次に、ダミー変数を取得します。

dummy = pd.get_dummies(merge_data[['Sex', 'Embarked']])
merge_data = pd.concat([merge_data.drop(['Sex', 'Embarked'], axis=1), dummy], axis=1)

そして今回は、nullが多く、前回の結果、予測にあまり影響がなかった「年齢」を学習対象から外します。

merge_data_sub1 = merge_data.drop(["Cabin", "Name", "Ticket", "Parch", "SibSp", "Age"], axis=1)

そして、結合したデータを訓練データとテストデータに再分割します。

train_data = merge_data_sub1[merge_data_sub1.Survived.isnull() == False]
test_data = merge_data_sub1[merge_data_sub1.Survived.isnull()]
train_data.info()
test_data.info()

<class 'pandas.core.frame.DataFrame'>
Int64Index: 891 entries, 0 to 890
Data columns (total 11 columns):
Fare           891 non-null float64
PassengerId    891 non-null int64
Pclass         891 non-null int64
Survived       891 non-null float64
have_family    891 non-null int64
is_alone       891 non-null int64
Sex_female     891 non-null uint8
Sex_male       891 non-null uint8
Embarked_C     891 non-null uint8
Embarked_Q     891 non-null uint8
Embarked_S     891 non-null uint8
dtypes: float64(2), int64(4), uint8(5)
memory usage: 53.1 KB

<class 'pandas.core.frame.DataFrame'>
Int64Index: 418 entries, 0 to 417
Data columns (total 11 columns):
Fare           417 non-null float64
PassengerId    418 non-null int64
Pclass         418 non-null int64
Survived       0 non-null float64
have_family    418 non-null int64
is_alone       418 non-null int64
Sex_female     418 non-null uint8
Sex_male       418 non-null uint8
Embarked_C     418 non-null uint8
Embarked_Q     418 non-null uint8
Embarked_S     418 non-null uint8
dtypes: float64(2), int64(4), uint8(5)
memory usage: 24.9 KB

テストデータのFareに一つのNULL値があるので、前回同様に平均値で埋めます。

test_data.Fare = test_data.fillna(test_data.Fare.mean())

それでは、GridSearchCVを使って最適なパラメータを探してみます。今回は、正則化強度のCを変化させてみようと思います。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV

param_grid = {'C' : [0.001, 0.01, 0.1, 1, 10, 100]}

grid_search = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid_search.fit(train_data.drop('Survived', axis=1), train_data['Survived'])

print("Best parameters : {}".format(grid_search.best_params_))
print("Best cross-validation score : {:.3f}".format(grid_search.best_score_))

Best parameters : {'C': 10}
Best cross-validation score : 0.779

なんと前回と学習データに対する精度が変わっていません（笑）
しかし、一旦テストデータに対しても予測をし、Kaggleに採点してもらうことにします。

lr = LogisticRegression(C=10)
lr.fit(train_data.drop('Survived', axis=1), train_data['Survived'])

test_data['Survived'] = lr.predict(test_data)
submittion_file = test_data[['PassengerId', 'Survived']]
submittion_file.to_csv('my_first_submittion.csv', index=False)
スクリーンショット 2018-04-30 12.46.00.png

テストデータに対するスコアは4%程あげることができました。一応上がりはしましたが、微妙...

##終わりに
今回、かなり微妙な結果となってしまいました！
前半、数式について調べた段階での息切れ感が隠せませんでした！
今後、更にスコアを伸ばすべく、上位ランカーのKernel等を活用し、勉強します。

40
31
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
40
31

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?