要約の要約
今回要約するのは、
Wu, Wush Chi-Hsuan, Mi-Yen Yeh, and Ming-Syan Chen. 2015. “Predicting Winning Price in Real Time Bidding with Censored Data.” In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining - KDD ’15, 1305–14. New York, New York, USA: ACM Press. DOI: 10.1145/2783258.2783276.
です。
複数の DSP が参加している状態で、SSP側や他のDSPとで情報が非対称である状況で、勝率や落札できる価格を予測する方法を提案しています。
問題提起
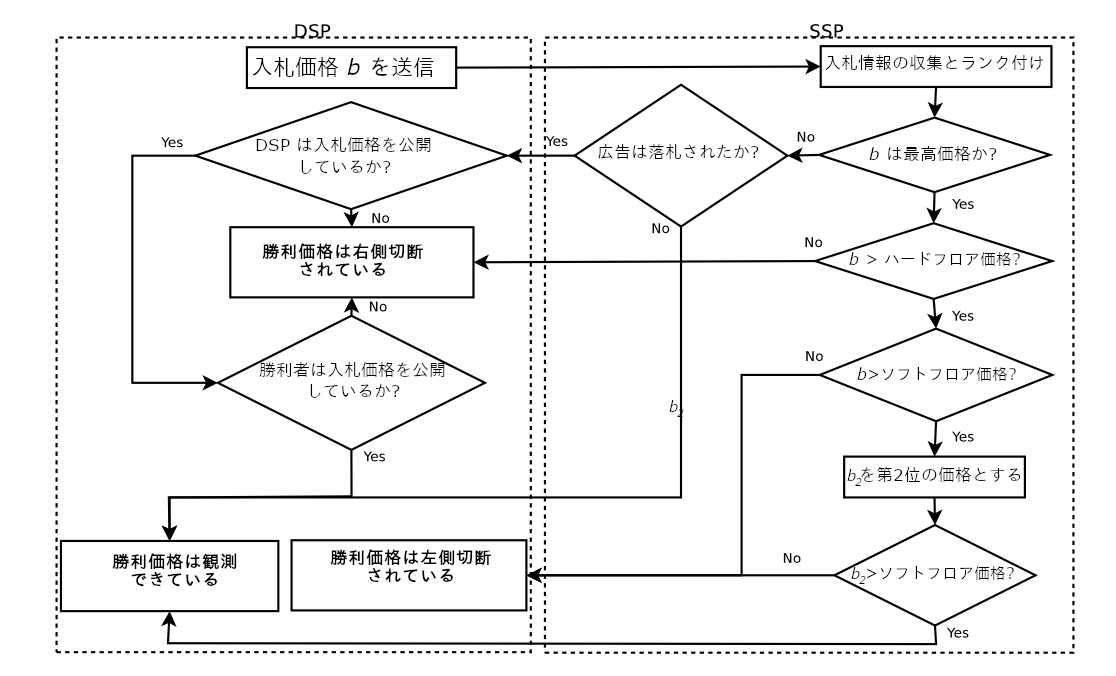
今回の問題を考える上で、広告ネットワークの状況を確認しておきます。以下、オークションに勝利するために最低限必要な入札価格のことを「勝利価格」と呼びます。広告ネットワークのオークションでは、これから説明するように入札時の価格と実際に請求される価格が異なるため、勝利価格は実際に払う「請求価格」とは必ずしも一致しません。
広告媒体主によってフロア価格が設定されている場合もあります。フロア価格とは、入札額の下限1で、ハードフロア価格とソフトフロア価格の2種類があります。もし、全てのDSPからの入札価格がいずれも、ハードフロア価格 $b_h$ を下回っている場合は、広告枠が売られることがありません。この場合は、勝利価格はハードフロア価格と同じとみなされます。もし1つでもハードフロア価格を上回った入札があれば、その入札価格が勝利価格になります。
RTB では、セカンドプライス (二位価格) オークションがよく利用されます。全DSP中で最も高い入札価格が $b$ で、 $b$ で入札した DSP 以外のDSPのうちで最高入札価格が $b_2$ なら、実際により少ない $b_2$ で入札しても勝利できたことになり、請求価格も $b_2$ となります。しかし、ここでソフトフロア価格設定が働くので、 $b_2$ は必ずしも勝利価格になりません。ソフトフロア価格 $b_s$ に対して、 $b_2 < b_s< b$ だった場合、$b_2$ ではなく $b_s$ が請求されます。こういう場合、落札者からは $b_2$ がわからないため、左側切断 (left-censored)データとなります。
最後のケースとして、オークションに敗北した場合、自分の入札価格は勝利価格より下である、ということしかわからず、右側切断 (right-censored) データとなります。
そのため、広告リクエストを特徴量に、オークションの勝敗をラベルにして回帰or分類モデルをそのまま当てはめて予測しようとするのは不適切だとわかります。
以上のメカニズムをフローチャートで表した、元論文の Fig. 1 を和訳して掲載します。
問題設定
次のように定式化しています。
$J$ 個の DSP $D_1, D_2, \cdots, D_J$ があり、そのうち $D_1$ が自分のDSPとします。広告リクエスト $i$ に対して、 $v_i$ を本当の勝利価格として、 $w_i$ を観測された価格とします。よって、よって、観測された価格と勝利価格の間には、以下のような関係があります。
$$
w_i = \begin{cases}
v_{1} & \text{if } D_1 \text{wins}\
0 & \text{otherwise}
\end{cases}
$$
また、 $D_1$ の入札価格を $b_i$ とします。広告リクエスト $i$ の特徴量 $x_i$ を、次のように3つに分割します。
- $x_i^1$: SSP 側から提供される情報
- $x_i^2$: $D_1$ が独自に得た情報
- $x_i^3$: 他の $D_j$ は知っているが、 $D_1$ は知らない情報
たとえば、ユーザータグは自信のDSPしか知らない情報のため、 $x_i^2$ に属します。
$D_j$ の入札戦略を $f_j(\cdot)$ と表します。すると、アドエクスチェンジは
$$
\left\{ f_1(x_i^1,x_i^2), f_2(x_i^1, x_i^3), \cdots, f_J(x_i^1, x_i^3) \right\}
$$
という入札を毎回受け取ります。ここで、ハードフロア価格が導入されているなら、上記にさらに $f_p(x_i^1)$ を追加します。ハードフロア価格の情報は SSP 側の情報なので、 $x_i^1$ によって決まる入札戦略に置き換えられます。よって、
$$
v_i = \max \left\{f_p(x_i^1), f_1(x_i^1,x_i^2), f_2(x_i^1, x_i^3), \cdots, f_J(x_i^1, x_i^3) \right\}
$$
となり、$D_1$ の入札価格が $v_i$ より大きければオークションに勝利できます。
方法
実際には、1つのDSPからは観測できない情報を含んでいます。そこでまずは、標準的な線形回帰
$$
v_i = \boldsymbol{x}_i^\top\boldsymbol{\beta} + \varepsilon_i
$$
を考えてみます。 $\boldsymbol{x}_i := \left\{ x_i^1, x_i^2 \right\}$ です。 $\varepsilon_i$ は正規誤差項です。しかし、実際に勝利価格がわかるのはオークションに勝ったときだけです。全体のうち、勝ったリクエストオークションを $W$ とし(これを観測データと呼びます)、これを負の対数尤度 (=損失関数)で評価すると、
$$
\sum_{i\in W} -\log\left(\phi\left(\frac{w_i - \boldsymbol{x}_i^\top\boldsymbol{\beta}_\mathit{lm}}{\sigma}\right)\right)
$$
となります。 $\phi()$ は標準正規分布の密度関数です。このモデルのパラメータを $\beta_\mathit{lm}$ と表し、以下モデルの略称としても使うことにします。
このやりかただと、オークションに敗北した場合のデータが一切使われません。実際に勝利した場合の勝利価格は、切断データよりも低くなります。
そこで、 Tobin (1958) によって提案された、いわゆる Tobit モデルを応用します。 $v_i = \boldsymbol{x}_i^\top\boldsymbol{\beta}$ から、$D_1$ の入札価格が勝利価格を上回る確率は
$$\begin{align}
\mathrm{P}(v_i<b_i) &= \mathrm{P}(\varepsilon_i < b_i - \boldsymbol{x}_i^\top\boldsymbol{\beta}) \
&= \Phi\left(\frac{b_i-\boldsymbol{\beta}^\top\boldsymbol{x}_i}{\sigma}\right)
\end{align}$$
と書けます。 $\Phi$ は標準正規分布の累積分布関数です。よって、入札価格が勝利価格を下回る確率もここから簡単に求められます。全体のうちオークションに負けたリクエストの集合を $L$ とすると (これを切断データと呼びます)、負の対数尤度は以下のようになります。
$$
\sum_{i\in W} -\log\left(\phi\left(\frac{w_i - \boldsymbol{x}_i^\top \boldsymbol{\beta}_\mathit{clm}}{\sigma}\right)\right) + \sum_{i\in L} -\log\left(\Phi\left(\frac{\boldsymbol{x}_i^\top \boldsymbol{\beta}_\mathit{clm} - b_i}{\sigma}\right)\right)
$$
これは(右)切断データに対応した線形回帰ということで、 $\beta_\mathit{clm}$ と表します。
オークションに負けた場合のデータも含んだため、$\beta_\mathit{lm}$ よりも良いやり方のように見えます。しかし、 $\beta_\mathit{lm}$ は勝利した場合のデータ (観測データ) に限定したパラメータで、 $\beta_\mathit{clm}$ は観測データだけでなく切断データについてのパラメータである、ということは、以下のような仮定を課していることになります。
観測データでの勝利価格のパターンと、切断データでの勝利価格のパターン (パラメータ) は同じである
そこで、この論文では、この仮定が成り立っていなくとも適用できるような「混合モデル」を提案しています。仮に、観測データと切断データとでパラメータが違うのならば、オークションに勝利した場合は当初の $\boldsymbol{\beta}_\mathit{lm}$, そうでない場合は $\boldsymbol{\beta}_\mathit{clm}$ がより適切になります。よって、
$$
\begin{align}
v_{i}=&\boldsymbol{x}_{i}^{\top}[\mathrm{P}(v_{i}<b_{i})\boldsymbol{\beta}_{lm}+(1-\mathrm{P}(v_{i}<b_{i}))\boldsymbol{\beta}_{\mathit{clm}}] \
=&\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta}_{\mathit{mix}}
\end{align}$$
と仮定します。すると、勝敗確率の式についても問題が発生します。すでに、 $v_i$ を $\beta_\mathit{lm}, \beta_\mathit{clm}$ と勝敗確率で定義してしまったため、このままの定義では使えません。そこで、正規分布ではなく、独自にロジスティック回帰を適用し、
$$
\mathrm{P}(v_i<b_i) = \frac{1}{1+\exp(-\boldsymbol{x}_i^\top\boldsymbol{\beta}_\mathit{lr})}
$$
とします。$\beta_\mathit{lr}$ はロジスティック回帰のパラメータです。
実験
この論文の前半部分で主張されていることを検証するポイントは、以下の3つです。
- 観測されたデータでの落札価格のパターンと、切断データでの落札価格のパターンは異なるのか
- 通常の線形回帰モデルよりも、切断回帰モデルのほうが良いモデルか
- 今回提案したモデルは切断回帰の欠陥を緩和し、既存のモデルの結果より改善されているか
以上3つの問題を、著者は実際のデータで検証しています。データは、iPinYou や、台湾のDSPサービス、 Bridgewell のものを使用しています。ソースコードは、 https://github.com/wush978/KDD2015wpp で公開されています。 R 言語で書かれています。
特徴量は、IP、地域、都市、アドエクスチェンジ、ドメイン、広告枠の大きさやフォーマット、といったカテゴリカルデータを、 feature hashing 変換したものを使用しています。さらに、同じ特徴量を使った CTR 予測モデルから得られた予測 CTR も特徴量として追加しています。
(1) については、データを二分割して、記述統計を比較したり、それぞれで(正則化)回帰した結果を比較して、傾向に大きな違いがあることを指摘しています。
(2) についても、 $\beta_\mathit{lm}$ と $\beta_\mathit{clm}$ を比較しています。 observed data に適用した場合、censored data に比べて平均的に勝利価格が低いため、 $\beta_\mathit{lm}$ では予測値に総じて下方バイアスがかかっています。一方で、 $\beta_\mathit{clm}$ は $\beta_\mathit{lm}$ より平均的に高い予測値を出しています。しかし、データによっては下振れが残るため、下方バイアスを完全に解消したとは言えません。全体的には、 $\beta_\mathit{clm}$ のほうが平均二乗誤差 (MSE) が小さい傾向にあります。
(3) 最後に、今回提案した $\beta_\mathit{mix}$ も加えて比較したところ、 $\beta_\mathit{mix}$ は $\beta_\mathit{lm}, \beta_\mathit{clm}$ のうち、いずれかより精度の良いほうに近く、ほとんどの場合で、切断データにおいて勝利価格の予測値のバイアスは、$\beta_\mathit{mix}$ のものが $\beta_\mathit{lm}$ より小さいという結果になりました。バイアスが大きくなりすぎたのは、 $\beta_\mathit{clm}$ が極端に過大に推定した場合で、それに引っ張られた結果だそうです。
$\beta_\mathit{lm}$ は切断データにおいて勝利か価格を過小推定してしまいますが、提案したモデルはこれをより適切に引き上げます。加えて、提案モデルは $\beta_\mathit{clm}$ よりも頑健であると言えます。
感想・講評
- いろいろ記号を用意している割に実際には使ってないことと、具体的な方法があまりスマートじゃないのが気になります。
- 実用的には、予算制約の概念も考慮した上で入札価格を決める方法のほうが良いのではないかと思います。つまり、 [論文要約] 入札価格の最適化について: "Optimal Real-Time Bidding for Display Advertising" で紹介したような方法です。
- 一方で、切断データを使っていることによるバイアスがあることを指摘しているのは重要で、この知見を他の最適化アルゴリズムに応用できる可能性があります。運用者、DSPのなど様々な立場から提案されている最適化アルゴリズムは、どれも勝率関数を過去の履歴にあてはめるという方法を採用しているので、この論文で説明されている入札価格分布の特徴を応用できるかもしれません。
参考文献
- Tobin, James. 1958. “Estimation of Relationships for Limited Dependent Variables.” Econometrica 26 (1): 24. DOI: 10.2307/19073822.
-
オークション理論では、留保価格 (reserve price) と呼ばれることが多いです。 ↩
-
ディスカッション・ペーパー版が無料でダウンロードできます。 ↩