はじめに
モンテカルロ法でπの近似値を求めるミニアプリをJSで作りました。
モンテカルロ法とは
モンテカルロ法とは、確率と統計に基づき乱数を利用して複雑な問題の近似解を求める手法で、元々は原子炉のシミュレーションに使われていました。この方法の考案には、1940年代にジョン・フォン・ノイマンとスタニスワフ・ウラムが関わり、第二次世界大戦中のマンハッタン計画での原子炉挙動予測に活用されました。モナコのカジノ名に由来し、現在では金融工学や物理、工学など多分野で応用されています。
円周率(π)を推定するステップ
-
ランダムな点を生成する
正方形の範囲内(キャンバス全体)に、ランダムな位置の点を連続的に生成し、プロットします。 -
条件を満たす点をカウントする
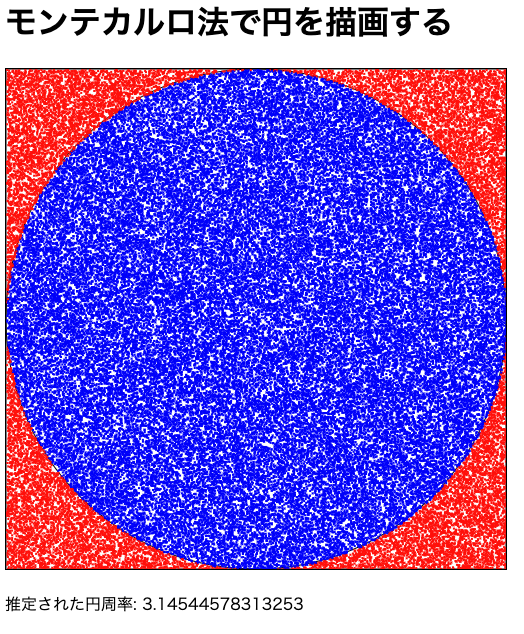
各点が円の内部か外部かを判定します。円の中心からその点までの距離が、円の半径より小さい場合であれば「円の中」とみなし、カウントを増やします。円の内側の点は青、外側の点は赤で描画されます。 -
比率を計算して円周率を推定する
円内にある点の数を、全体の点の数で割り、その比率を用いて円周率を近似します。円が正方形に内接している場合、この比率はπ/4に近づくため、円周率の推定にはこの比率を4倍した値を利用します。
コード
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Monte Carlo Circle</title>
<style>
canvas {
border: 1px solid black;
}
</style>
</head>
<body>
<h1>モンテカルロ法で円を描画する</h1>
<canvas id="monteCarloCanvas" width="500" height="500"></canvas>
<p id="piValue"></p>
<script>
// キャンバスとコンテキストの取得
const canvas = document.getElementById('monteCarloCanvas');
const ctx = canvas.getContext('2d');
const width = canvas.width; // キャンバスの幅
const height = canvas.height; // キャンバスの高さ
const radius = width / 2; // 円の半径(キャンバスの半分)
let insideCircle = 0; // 円の中に入った点の数
let totalPoints = 0; // 全体の点の数
// 正方形と円を描画
ctx.strokeRect(0, 0, width, height); // 外枠の正方形を描画
ctx.beginPath();
ctx.arc(radius, radius, radius, 0, Math.PI * 2); // 円を描画
ctx.stroke();
// モンテカルロ法で点をランダムに描画
function monteCarlo() {
for (let i = 0; i < 1000; i++) {
// ランダムな点のx, y座標を生成
const x = Math.random() * width;
const y = Math.random() * height;
// 点と円の中心との距離を計算
const dist = Math.sqrt(Math.pow(x - radius, 2) + Math.pow(y - radius, 2));
// 距離が半径より小さい場合、円の中にある
if (dist < radius) {
insideCircle++;
ctx.fillStyle = 'blue'; // 円の中は青色
} else {
ctx.fillStyle = 'red'; // 円の外は赤色
}
// 点を描画(小さな四角形で表現)
ctx.fillRect(x, y, 2, 2);
totalPoints++;
}
// モンテカルロ法で円周率の近似値を計算
const piEstimate = (insideCircle / totalPoints) * 4;
document.getElementById('piValue').textContent = `推定された円周率: ${piEstimate}`;
}
// 一定間隔でモンテカルロ法を実行
setInterval(monteCarlo, 100);
</script>
</body>
</html>