初心者向け（小学生の算数で解くプログラミング）

#はじめに
先日、twitterでみかけた「任意の自然数の各桁を、一桁になるまで掛け算する回数の最大回数とその数を示せ。」という課題をお子様がpythonで解いたというツイートに触発されて、僕も子供にプログラミングを教えたいと思って作ったものです。
小学生の算数の知識と少しのプログラミングの知識でできるようにしています。
いまだに、夏休みの自由研究が終わっていないお子様にいかがでしょうか。
なお、GAS（JavaScript）を使用しています。

###必要な知識
四則演算（+-*/）、小数点以下切り下げ（Math.Floor()）
変数（小学生が対象のためローマ字で書いています）
whileによる繰り返し
forによる繰り返し
ifによる条件分岐
（最後に少しだけ配列を使います）

#１．二桁（10〜99）の計算
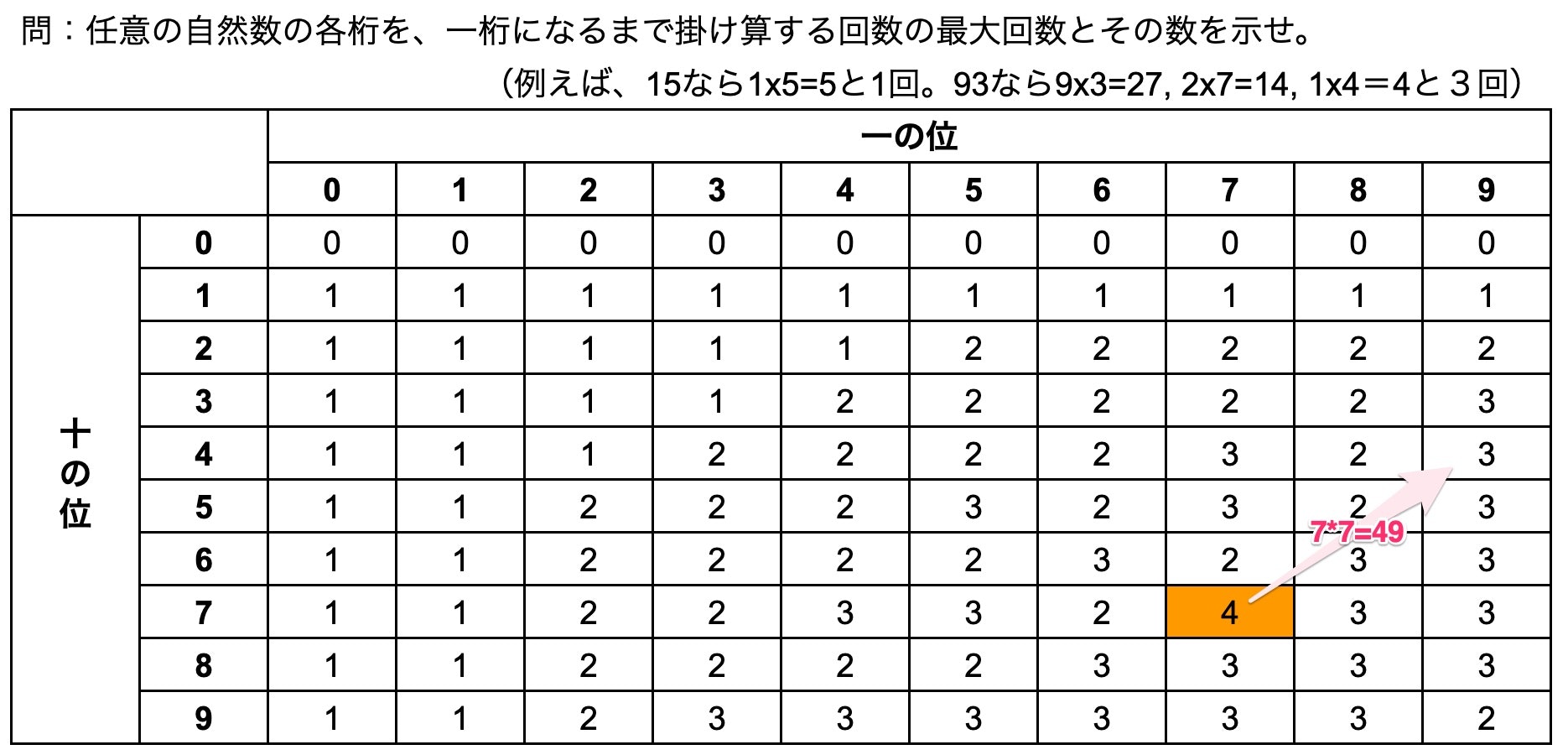
冒頭でも書きましたが、「任意の自然数の各桁を、一桁になるまで掛け算する回数の最大回数とその数を示せ。」という問いに対し、二桁の場合の掛け算する回数の最大回数とその数はいくつでしょうか。

これは、時間があれば自分で計算して解いてほしいと思います。いろいろな規則性が見えてくるかもしれません。

####回答

答えは７７（７７⇛49⇛36⇛18⇛8）で4回です。

#2．複数桁の計算（各桁の数字の抽出方法）
三桁からはどうやら時間がかかりそうなのでプログラムを利用します。
各桁の数字を抽出するにはどのようにすればよいでしょうか。
四則演算と小数点以下切り下げを利用します。
例として「679」を分解する方法を考えます。

やり方としては単純に１０で割って小数点以下を切り下げてもとの数字から引くだけです。

いろいろな数字が使いまわせそうです。これをプログラムにしてみます。

function threeDigits() {
  var kazu = 679
  var warizan
  
  warizan = Math.floor(kazu/10)       //679÷10＝67.9⇛⇛⇛67（小数点以下切り下げ）
  var ichi = kazu - warizan * 10      //679　−　67×10＝9（一の位の数）
  Logger.log(ichi)
  
  kazu = warizan
  warizan = Math.floor(kazu/10)       //67÷10＝6.7⇛⇛⇛6（小数点以下切り下げ）
  var zyuu = kazu - warizan * 10      //67−6×10＝7（十の位の数）
  Logger.log(zyuu)                    
  
  var hyaku = warizan                 //6（百の位の数）
  Logger.log(hyaku)                    
 
  Logger.log(ichi * zyuu * hyaku)     //一の位の数×十の位の数×百の位の数=378
}

しかし、これは三桁の数の計算しかできませんので、使い物になりません。いろいろな桁数に対応できるように「whileによる繰り返し」を使ってみます。

function multiDigits() {
  var kazu = 679                       //最初の数
  var kotae = 1                        //各桁をかけ合わせた数、初期値は１

  do{
    var warizan = Math.floor(kazu/10)  //10で割って小数点以下を切り下げ
    var kakuketa = kazu - warizan * 10 //各桁の数字
    kotae = kotae * kakuketa           //各桁をかけ合わせた数
    kazu = warizan                     //一桁少なくして再計算
  }while(kazu>0)                       //最終的に数が０になるまで繰り返し

  Logger.log(kotae)
}

ずいぶんすっきりしました。これで何桁でも計算できます。

#3．結果が一桁になるまで掛け算する
問題は一桁になるまで掛け算する回数の最大回数とその数を示すことでしたが、これでは１回しか計算できないので、１桁になるまで繰り返すように計算します。これも同様に「whileによる繰り返し」を利用します。

function calcMultiDigits() {
  var kazu = 679                         //最初の数
  var kaisuu = 0                         //計算回数
  do{
    var kotae = 1                        //各桁をかけ合わせた数
    do{
      var warizan = Math.floor(kazu/10)  //10で割って小数点以下を切り下げ
      var kakuketa = kazu - warizan * 10 //各桁の数字
      kotae = kotae * kakuketa           //各桁をかけ合わせた数
      kazu = warizan                     //一桁少なくして再計算
    }while(kazu>0)                       //最終的に数が０になるまで繰り返し
      Logger.log(kotae)
      kaisuu = kaisuu + 1                //１回計算するごとに回数の変数を増やしていく
      kazu = kotae                       //求めた答えをもとに再計算
  }while(kotae>=10)                      //一桁になるまで繰り返す
  Logger.log(kaisuu + '回計算')
}

/*結果
378.0
168.0
48.0
32.0
6.0
5回計算
*/

これで理論上は何桁でも計算できるようになりました。
#４．繰り返し計算をする
これでひたすら繰り返し計算する土台ができました。あとは「forによる繰り返し」でひたすらコンピュータで計算するだけです。ためしに１００までやってみます。

function calcMultiDigitsWithItr() {
  
  for(kurikaeshi = 10;kurikaeshi<100;kurikaeshi++){      //10から９９まで繰り返し
    var kazu = kurikaeshi                  
    var kaisuu = 0                         //計算回数
    do{
      var kotae = 1                        //各桁をかけ合わせた数
      do{
        var warizan = Math.floor(kazu/10)  //10で割って小数点以下を切り下げ
        var kakuketa = kazu - warizan * 10 //各桁の数字
        kotae = kotae * kakuketa           //各桁をかけ合わせた数
        kazu = warizan                     //一桁少なくして再計算
      }while(kazu>0)                       //最終的に数が０になるまで繰り返し
        kaisuu = kaisuu + 1                //１回計算するごとに回数の変数を増やしていく
        kazu = kotae                       //求めた答えをもとに再計算
    }while(kotae>=10)                      //一桁になるまで繰り返す
      Logger.log(kurikaeshi + '----->' + kaisuu + '回計算')
      }
}
/*結果
75----->3回計算
76----->2回計算
77----->4回計算
78----->3回計算
79----->3回計算
*/

いい感じです。では、最大の計算回数とその時の数字、あとはタイマーを追加します。

function calcMultiDigitsWithTimer() {
  var saidaiKaisuu = 0                               //最大の計算回数
  var saidaiSuu                                      //そのときの数
  var zikan = new Date()                             //時間計測用
  for(kurikaeshi = 10;kurikaeshi<3000000;kurikaeshi++){     //10から299９９99まで繰り返し
    var kazu = kurikaeshi                  
    var kaisuu = 0                         //計算回数
    do{
      var kotae = 1                        //各桁をかけ合わせた数
      do{
        var warizan = Math.floor(kazu/10)  //10で割って小数点以下を切り下げ
        var kakuketa = kazu - warizan * 10 //各桁の数字
        kotae = kotae * kakuketa           //各桁をかけ合わせた数
        kazu = warizan                     //一桁少なくして再計算
      }while(kazu>0)                       //最終的に数が０になるまで繰り返し
        kaisuu = kaisuu + 1                //１回計算するごとに回数の変数を増やしていく
        kazu = kotae                       //求めた答えをもとに再計算
    }while(kotae>=10)                      //一桁になるまで繰り返す
      if(kaisuu > saidaiKaisuu){           //もし回数が最大回数より大きければ
        saidaiKaisuu = kaisuu              //最大回数を更新
        saidaiSuu = kurikaeshi             //その時の数を記録
      }
      }
  Logger.log(saidaiSuu + 'のときに' + saidaiKaisuu + '回')
  Logger.log((new Date() - zikan)/1000 + '秒')
}
/*結果
2677889のときに8回
244.07秒
*/

ためしに２９９９９９９まで計算してみました。４分くらいかかりましたがいい結果が出ました。

#5.もっと処理を速くしたい（配列の利用）
さらに計算の回数を少なくして処理時間を速くしてみます。
各桁を掛け算した結果はもとの自然数よりかならず少ない数になります。少ない数から始めて、結果をメモしていけば、過去の結果を利用することができます。

例として77を考えます。７７の計算は77=49です。これまでの計算ではさらに49を49=36、36を3*6…としましたが、最初から49の結果は３と判明しているため過去の結果をメモしていれば再計算の必要はありません。つまり、過去の結果をメモしていれば上記「３．結果が一桁になるまで掛け算する」をする必要はなく、過去の記録+1回が答えです。これをプログラムにしてみます。

function calcMultiDigitsWithDP() {
  var memo = new Array()                             //記録用配列
  for(i=0;i<10;i++){
  memo[i] = 0                                        //１桁目の答えは0でるために配列にいれておく
  }
  
  var saidaiKaisuu = 0                               //最大の計算回数
  var saidaiSuu                                      //そのときの数
  var zikan = new Date()                             //時間計測用
  for(kurikaeshi = 10;kurikaeshi<3000000;kurikaeshi++){    //10から299９９99まで繰り返し
    var kazu = kurikaeshi                  

      var kotae = 1                        //各桁をかけ合わせた数
      do{
        var warizan = Math.floor(kazu/10)  //10で割って小数点以下を切り下げ
        var kakuketa = kazu - warizan * 10 //各桁の数字
        kotae = kotae * kakuketa           //各桁をかけ合わせた数
        kazu = warizan                     //一桁少なくして再計算
      }while(kazu>0)                       //最終的に数が０になるまで繰り返し
        var kaisuu = 1 + memo[kotae]       //計算回数 過去の記録+1回
        memo[kurikaeshi] = kaisuu          //記録を配列に入れる。
      if(kaisuu > saidaiKaisuu){           //もし回数が最大回数より大きければ
        saidaiKaisuu = kaisuu              //最大回数を更新
        saidaiSuu = kurikaeshi             //その時の数を記録
      }
      }
  Logger.log(saidaiSuu + 'のときに' + saidaiKaisuu + '回')
  Logger.log((new Date() - zikan)/1000 + '秒')
}
/*結果
2677889のときに8回
227.922秒
*/

ちょっと速くなりました。
さらに速くする余地はまだありそうですが、とりあえずはここまでにします。

以上です。最後まで読んでいただきありがとうございました。