論理パズルをプログラムで解く

はじめに

このツイートにあった論理パズルをプログラムを使って解いてみます。Swift Playgroundを使用します。

この投稿では、「集合（セット）」、「組み合わせ（nCr）」の知識が必要です。
ちなみに、この論理パズルはわざわざプログラムで解くより自分で解を考えたほうが遥かに効率的です。

問題：
4人の人が真夜中に川にかかった吊り橋を渡ろうとしています。吊り橋に同時に乗ることができるのは最大二人です。それぞれの人の足の速さは大きく異なり、その橋を渡るにはそれぞれ１分、２分、５分、１０分が必要です。真っ暗なため、懐中電灯が必要ですが、一つしかないため、二人で渡る際には手を繋いで、遅い人に合わせたスピードで渡る必要があります。懐中電灯の電池が１７分しか残っていない場合、どうやったら全員で対岸に渡ることができるでしょう？

#１　問題を抽象化する
この問題は人がイメージしやすくするために、様々な情報が入っていますが、プログラムでは不要な部分が多いため取り除いてみます。

（１）　そもそも人であることを定義する必要はない。
（２）　別に真夜中であることを定義する必要はない。
（３）　吊り橋であることを定義する必要はない。
（４）　４人の足の速さはどうでもよく、橋を渡る時間が本質。
（５）　別に手を繋ぐ必要はない。
（６）　そもそも時間の単位が「分」である必要もない

これらの要素はプログラムには関係ありません。
要するに、移動のたびに経過時間（２人の場合は高いほう）を足していき、最終的に終点にすべての人が移動すれば終了です。
ただ、橋の両端の名前が定義されていませんので、始点をpointA、終点をpointBと名付けます。

#２　何種類のパターンが考えられるか
橋を渡りきるには様々なパターンが考えられますが、何種類くらいあるでしょうか。
２人行って１人帰って…と繰り返すと、２．５往復（５ターン）かかることがわかり、その場合の組み合わせは次のようになります。なお、例外なくすべての組み合わせを考えます。

	pointA	pointB	行　動	組み合わせ
1ターン目	4人	0人	AからBへ２人移動	${}_4C_2$ = 6
2ターン目	2人	2人	BからAへ1人移動	${}_2C_1$ = 2
3ターン目	3人	1人	AからBへ２人移動	${}_3C_2$ = 3
4ターン目	1人	3人	BからAへ1人移動	${}_3C_1$ = 3
5ターン目	2人	2人	AからBへ２人移動	${}_2C_2$ = 1
終　了	0人	4人

この組み合わせをかけ合わせた数、つまり、$62331 = 108$ 種類の組み合わせが存在します。
この108種類をすべてプログラムで求めます。

３　プログラムを作っていく

##(1) 組み合わせ（nCr）をプログラムする
このプログラムでは組み合わせ（nCr）を多用するので、先に組み合わせを作成するプログラムを作っておきます。
「集合n」から「r人」取り出すので、この２つを引数として「集合の集合」を戻り値とする関数とします。
①引数nの要素数の数繰り返す関数をr回再帰させます。${}_4C_2$であれば、$4^2$回の計算を行い、それぞれの集合を作っていきます。
②出来上がった集合のうち、要素数がｒのものだけ、戻り値の集合に入れます。
③戻り値の集合は、重複を排除するので、最終的にはユニークな集合のみが残ります。

nCr.swift

import UIKit

func nCr<T>(n:Set<T>,r:Int)->Set<Set<T>>{                  //引数nは集合、rは整数、戻り値は集合の集合（ジェネリクス）
    var results:Set<Set<T>> = []                           //戻り値用の変数(results)
    func rec(itr:Int,result:Set<T>){                       //再帰関数。引数は再帰回数itrと作成中の集合result
        guard itr<r else{                                  //他の言語のwhileみたいなの。rがitrと同じになれば再帰終了。
            result.count == r ? results.insert(result):nil //出来上がった集合resultの要素数がrであれば、resultsに代入
            return
        }
        for num:T in n{                                    //関数nCrの要素をひとつずつ取り出す。
            var myResult:Set<T> = result                   //次の再帰関数の引数用の集合myResultを用意
            myResult.insert(num)                           //myResultに集合nから取り出した要素numを追加
            rec(itr: itr + 1, result: myResult)            //再帰させる
        }
    }
    rec(itr: 0, result: [])                                //再帰関数の開始
    return results
}

ためしに[1,2,5,10]から2つ取り出す組み合わせを作ってみましょう。${}_4C_2$＝６種類の集合ができるはずです。

print(nCr(n: [1,2,5,10], r: 2))
//[Set([1, 10]), Set([10, 2]), Set([10, 5]), Set([2, 1]), Set([5, 1]), Set([2, 5])]

うまくできました。
ちなみに、汎用性を高めるために戻り値はジェネリクスにしていますので、「６人のクラスの中から３人選ぶ」みたいな組み合わせもこんな感じでできます。

print(nCr(n: ["佐藤","鈴木","吉田","高橋","山本","斎藤"],r: 3))
//[Set(["山本", "高橋", "吉田"]), Set(["鈴木", "佐藤", "吉田"]), Set(["鈴木", "高橋", "吉田"]), Set(["吉田", "佐藤", "高橋"]), Set(["吉田", "斎藤", "高橋"]), Set(["鈴木", "山本", "高橋"]), Set(["鈴木", "佐藤", "高橋"]), Set(["山本", "佐藤", "高橋"]), Set(["鈴木", "斎藤", "吉田"]), Set(["山本", "佐藤", "斎藤"]), Set(["山本", "斎藤", "吉田"]), Set(["鈴木", "佐藤", "斎藤"]), Set(["鈴木", "山本", "佐藤"]), Set(["吉田", "佐藤", "斎藤"]), Set(["鈴木", "山本", "吉田"]), Set(["鈴木", "斎藤", "高橋"]), Set(["山本", "斎藤", "高橋"]), Set(["鈴木", "山本", "斎藤"]), Set(["高橋", "佐藤", "斎藤"]), Set(["山本", "佐藤", "吉田"])]

${}_6C_3$＝20種類の集合ができました。

##(2) 橋を移動するプログラムを作ってみる
では、pointAとpointBを往復するプログラムを考えます。
###①pointAからpointBへ移動する関数

• pointAにいる人の中から２人選ぶ集合を作る。
• この２人をpointBへ移動させる
• この２人の内、足が遅い人の時間を調べて合計時間に加える
• 「pointBからpointAへ移動する関数」を集合の数だけ再帰する

###②pointBからpointAへ移動する関数

• pointBにいる人の中から1人選ぶ集合を作る。
• この人をpointAへ移動させる
• この人の時間を調べて合計時間に加える
• 「pointAからpointBへ移動する関数」を集合の数だけ再帰する

この①と②を繰り返して最終的にはpointAの人が０人になれば終了です。

ここで注目したいのが①の関数と②の関数は移動する方向が違うだけでほぼ同じ機能を持っています。
よって、向きを決める変数（Bool）を用意しておけば、一つの関数でできるはずです。
ちなみに、この変数（Bool）こそが、「懐中電灯」の役割となります。
###橋を移動する関数
できたのが次の関数です。

moveRec.swift

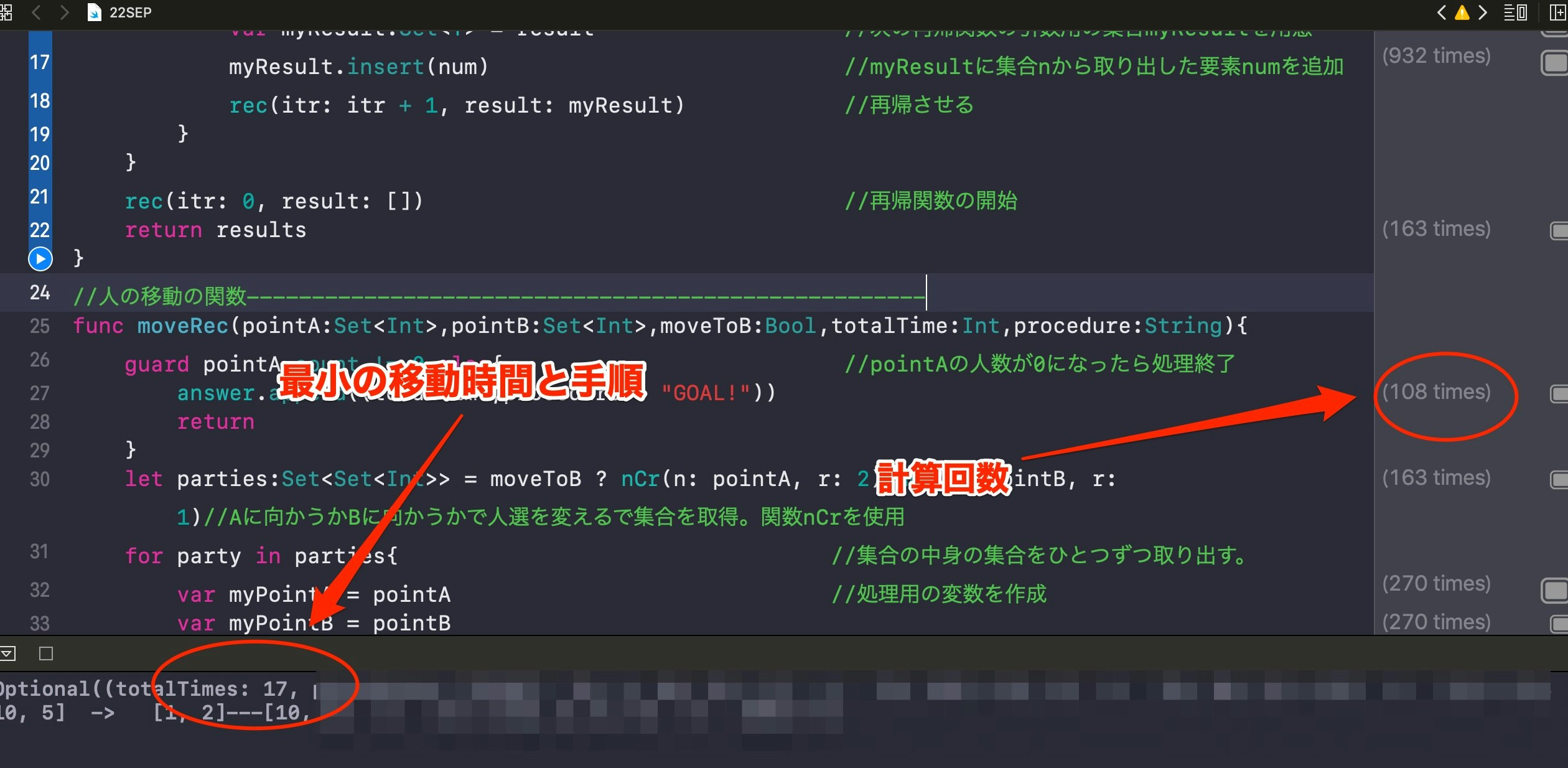
func moveRec(pointA:Set<Int>,pointB:Set<Int>,moveToB:Bool,totalTime:Int,procedure:String){
    guard pointA.count != 0 else{                          //pointAの人数が0になったら処理終了
        answer.append((totalTime,procedure + "GOAL!"))
        return
    }
    let parties:Set<Set<Int>> = moveToB ? nCr(n: pointA, r: 2):nCr(n: pointB, r: 1)//Aに向かうかBに向かうかで人選を変えるで集合を取得。関数nCrを使用
    for party in parties{                                 //集合の中身の集合をひとつずつ取り出す。
        var myPointA = pointA                             //処理用の変数を作成
        var myPointB = pointB
        moveToB ? party.map({(num:Int) in myPointA.remove(num);myPointB.insert(num)}):party.map({(num:Int) in myPointA.insert(num);myPointB.remove(num)})
        //人の移動のための関数。わかりにくいっすね。すいません。
        let myTotalTime = totalTime + party.max()!        //経過時間を計算
        let addProcedure:String = procedure + "\(myPointA)---\(myPointB)  ->   "//結果出力用の文字列を作っておく
        moveRec(pointA: myPointA, pointB: myPointB, moveToB: !moveToB, totalTime: myTotalTime, procedure: addProcedure)//移動の向き(moveToB)を変えて再帰する
    }
}

##(3) 完成形
（１）と（２）をあわせて、初期値を加えたプログラムがこれです。

.swift

import UIKit
//初期値----------------------------------------------------
let initialPointA:Set<Int> = [1,2,5,10]                                         //pointAの初期位置
let initialPointB:Set<Int> = []                                                 //pointBの初期位置
let initialString:String = "START!  \(initialPointA)---\(initialPointB)  ->   " //結果の文字列の初期値
var answer:[(totalTimes:Int,procedures:String)] = []                            //結果格納用変数
//組み合わせを求める関数----------------------------------------------------
func nCr<T>(n:Set<T>,r:Int)->Set<Set<T>>{                  //引数nは集合、rは整数、戻り値は集合の集合（ジェネリクス）
    var results:Set<Set<T>> = []                           //戻り値用の変数(results)
    func rec(itr:Int,result:Set<T>){                       //再帰関数。引数は再帰回数itrと作成中の集合result
        guard itr<r else{                                  //他の言語のwhileみたいなの。rがitrと同じになれば再帰終了。
            result.count == r ? results.insert(result):nil //出来上がった集合resultの要素数がrであれば、resultsに代入
            return
        }
        for num:T in n{                                    //関数nCrの要素をひとつずつ取り出す。
            var myResult:Set<T> = result                   //次の再帰関数の引数用の集合myResultを用意
            myResult.insert(num)                           //myResultに集合nから取り出した要素numを追加
            rec(itr: itr + 1, result: myResult)            //再帰させる
        }
    }
    rec(itr: 0, result: [])                                //再帰関数の開始
    return results
}
//人の移動の関数----------------------------------------------------
func moveRec(pointA:Set<Int>,pointB:Set<Int>,moveToB:Bool,totalTime:Int,procedure:String){
    guard pointA.count != 0 else{                          //pointAの人数が0になったら処理終了
        answer.append((totalTime,procedure + "GOAL!"))
        return
    }
    let parties:Set<Set<Int>> = moveToB ? nCr(n: pointA, r: 2):nCr(n: pointB, r: 1)//Aに向かうかBに向かうかで人選を変えるで集合を取得。関数nCrを使用
    for party in parties{                                 //集合の中身の集合をひとつずつ取り出す。
        var myPointA = pointA                             //処理用の変数を作成
        var myPointB = pointB
        moveToB ? party.map({(num:Int) in myPointA.remove(num);myPointB.insert(num)}):party.map({(num:Int) in myPointA.insert(num);myPointB.remove(num)})
        //人の移動のための関数。わかりにくいっすね。すいません。
        let myTotalTime = totalTime + party.max()!        //経過時間を計算
        let addProcedure:String = procedure + "\(myPointA)---\(myPointB)  ->   "//結果出力用の文字列を作っておく
        moveRec(pointA: myPointA, pointB: myPointB, moveToB: !moveToB, totalTime: myTotalTime, procedure: addProcedure)//移動の向き(moveToB)を変えて再帰する
    }
}
//実行、結果表示用----------------------------------------------------
moveRec(pointA: initialPointA, pointB: initialPointB, moveToB: true, totalTime: 0, procedure: initialString)
print(answer.min(by: {(a,b) -> Bool in return a.totalTimes < b.totalTimes}))//最小値を出力

#4　結果
実際に動かしてみた結果です。

計算の回数は、予想通り１０８回でした。つまり、すべてのパターンを計算したことになります。
最小の時間も１７分であり、そのときの手順も表示できています。（画像ではモザイクをかけています）

#おわりに
冒頭でも書きましたが、この論理パズルは頭で考えたほうが遥かに速く解けます。直感であっという間に解いてしまう人もいるでしょう。
ただし、問題の本質を抜き出し、論理的に分解することは時間がかかっても非常に重要ではないかと個人的には思います。
僕はエンジニアでもなんでもないですが、物事から本質を抽出できない大人がどの世界でも多すぎると感じます。
まあ、どうでもいいですけどね。

読んでいただきありがとうございました！