樹木曲線をベジェ曲線で描く

#はじめに
なぜ、樹木曲線は、曲線って書いておきながら直線なんでしょうか？
気になったのでベジェ曲線で樹木曲線を描いてみます。
完成図は、こんな感じです。
ベジェ曲線を使って、枝の継ぎ目がなめらかになるようにしています。

なお、swiftを使っています。

#１　樹木曲線

###(1)弧度法と三角関数
樹木曲線を描くためにはどうしても弧度法と三角関数を理解する必要があります。
ここですでに嫌になってしまう人もいるかも知れませんが、覚えるのはこの2つだけです。

• $360^\circ=2*\pi$ つまり $1^\circ=\pi/180$

• x軸は$cos$、y軸は$sin$

たったこれだけです。

###(2)再帰関数
複雑な図で説明してもわかりにくいため、次のシンプルな図で説明します。

二股に別れた枝が更に…を3回繰り返しているのがわかるかと思います。
それぞれの線を描画するわけですが、どういう順番で描画しているか想像できるでしょうか。
実は、こういう順番で書かれています。想像していた順番と違った人もいるかと思います。

これが、再帰関数の特徴です。
再帰関数については詳しく書きませんが、この順番を意識すると理解が深まります。

###(3)ベジェ曲線を使って継ぎ目をなめらかに
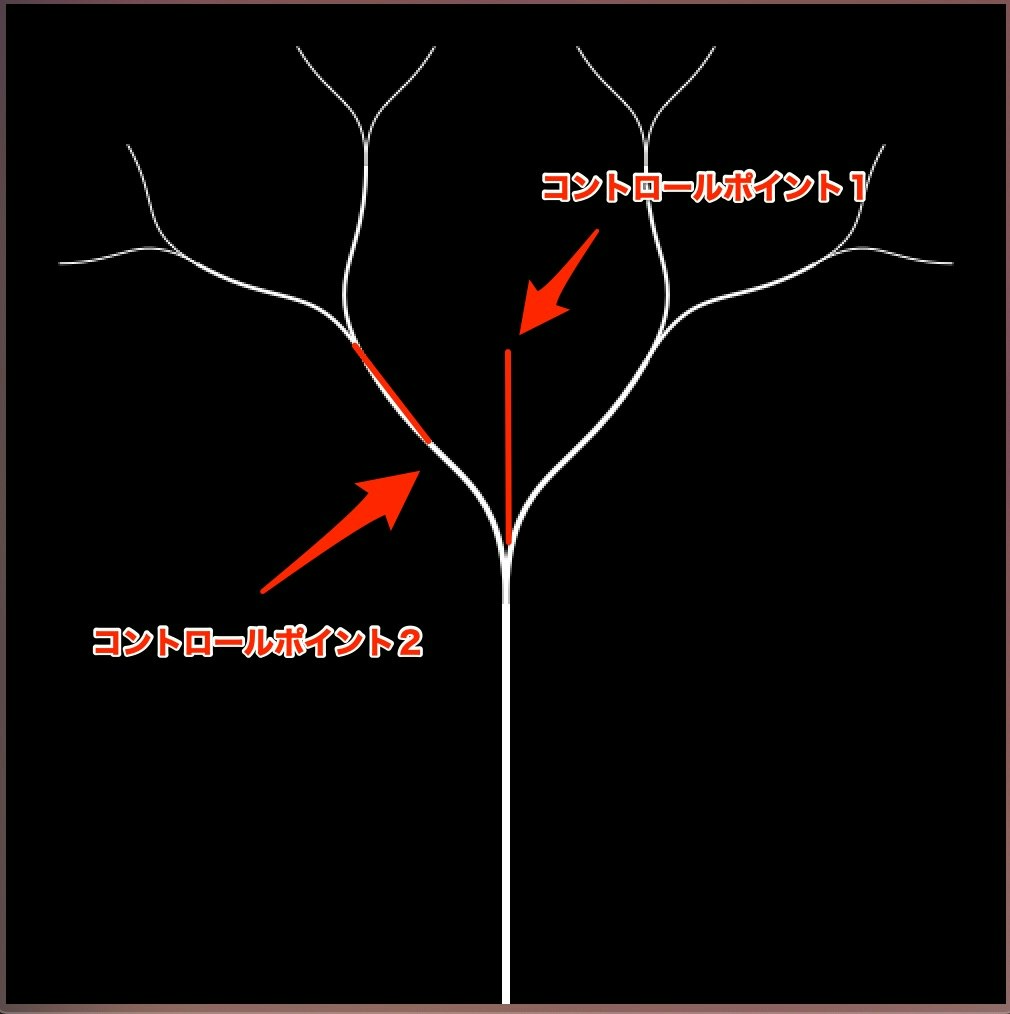
swiftのベジェ曲線の描画ではコントロールポイントを２つ設定できますが、どのようにすれば、これらをうまく使ってなめらかな曲線を描くことができるでしょうか。
答えは、描画する線の始点（つまり前の線の終点）の延長線上にひとつめのコントロールポイント（コントロールポイント１）を、ふたつめのコントロールポイント（コントロールポイント２）を描画する線の終点の手前におけば始点と終点の角度が前後の線の角度と同じになるためなめらかになります。

#２ 完成図
細かい話を描くと長くなってしまいますのでいきなり完成図です。
swift playgroundにコピーするとうまくいくと思います。
実質４０行くらいの短いコードです。４から１０行目までのパラメータを変えると変化した樹木曲線が確認できます。

fractalTree.swift

import UIKit
let RAD:CGFloat = CGFloat.pi/180.0//１°＝π/180[rad]
//各パラメータ
let pictureSize:CGFloat = 500.0//画像の一辺の大きさ
let angleWidth:[CGFloat] = [5.0,5.0,30.0,20.0,10.0,10.0,30.0,50.0]//枝分かれの角度
let offsetAngle:CGFloat = 30.0//オフセットの角度
let recNum:Int = 4//再帰回数
let initialLength:CGFloat = 200.0//最初の枝の長さ
let initialAngle:CGFloat = 270.0//最初の枝の角度
let branchRatio:CGFloat = 0.7//次の枝の長さの比率

func drawTree()->UIImage{
    //枝の角度の再計算
    var convertedAngle:[CGFloat] = [0.0]
    let sumOfAngle:CGFloat = angleWidth.reduce(0,{(num1: CGFloat, num2: CGFloat) -> CGFloat in
        convertedAngle.append(num1 + num2)
        return num1 + num2})
    convertedAngle = convertedAngle.map{($0 - 0.5 * sumOfAngle + offsetAngle) * RAD}
    //x座標、ｙ座標計算用クロージャ
    let calcPoint = {(point:CGPoint ,angle:CGFloat,length:CGFloat) -> CGPoint in
        return CGPoint(x: point.x + cos(angle) * length, y: point.y + sin(angle) * length)}
    //再帰関数
    func recDrawLine(recNum:Int,startPoint:CGPoint,newAngle:CGFloat,oldAngle:CGFloat,length:CGFloat){
        guard recNum != 0 else{
            return
        }
        let drawPath = UIBezierPath()
        drawPath.lineWidth = CGFloat(recNum)
        //終点、コントロールポイントの計算
        let endPoint:CGPoint =      calcPoint(startPoint,newAngle,length)
        let controlPoint1:CGPoint = calcPoint(startPoint,oldAngle,length *  0.5)
        let controlPoint2:CGPoint = calcPoint(endPoint,  newAngle,length * -0.5)
        //ベジェ曲線の描画
        drawPath.move(to: startPoint)
        drawPath.addCurve(to: endPoint, controlPoint1: controlPoint1, controlPoint2: controlPoint2)
        drawPath.stroke()
        //枝分かれの数だけ再帰
        for i in 0..<convertedAngle.count{
            recDrawLine(recNum: recNum - 1, startPoint: endPoint , newAngle: newAngle + convertedAngle[i], oldAngle: newAngle, length: length * branchRatio)
        }
    }
    //描画開始,線の色の決定
    UIGraphicsBeginImageContextWithOptions(CGSize(width: pictureSize, height: pictureSize), true, 1.0)
    UIColor.white.setStroke()
    //再帰関数開始
    recDrawLine(recNum: recNum, startPoint: CGPoint(x: pictureSize/2, y: pictureSize), newAngle: initialAngle * RAD , oldAngle: initialAngle * RAD, length: initialLength)
    //画像取得
    let image:UIImage = UIGraphicsGetImageFromCurrentImageContext()!
    //描画終了
    UIGraphicsEndImageContext()

    return image
}

let myUIImageView:UIImageView = UIImageView(image: drawTree())

ちなみに、上記はこんな感じです。

#おわりに

これを連続で表示させるようにしたアプリが、
FRACTALS TREE になります。
僕がはじめて作ったアプリです。無料ですのでもしよろしければダウンロードしてみてください。