LoginSignup
15
13

More than 1 year has passed since last update.

@s059ff

コンピュータにおける三角関数の実装

Posted at

コンピュータにおける三角関数の実装

※この文章は主に Intel社の文献 1 をもとに記述しています。

歴史的な話

1980年代に開発された Intel 8087 プロセッサーでは、sin cos を含む数学関数がハードウェア実装された。
現在の Intel や AMD の x86_64 アーキテクチャ CPU にも、互換性を維持する目的で実装され続けている。(x87)

しかしながら、最近のプログラミング言語で sin cos を呼び出しても、
これらの x87 命令が使用されることはなく、ソフトウェア的に計算が行われる。

それには、x87 命令の実装に使用されたアルゴリズムに、速度や精度上の欠点があるため、と言われている。

1 から引用

In the 1990s Intel replaced the 8087's CORDIC-based approximations of the elementary transcendental functions with polynomial-based approximations. These newer polynomial-based approximations provide a large degree of backwards compatibility with the CORDIC based approximations by approximating precisely the same functions, but with greater overall accuracy and speed.

具体的には、sinの場合 $x\approx\pi$ の場合に、誤差が大きくなるようである。

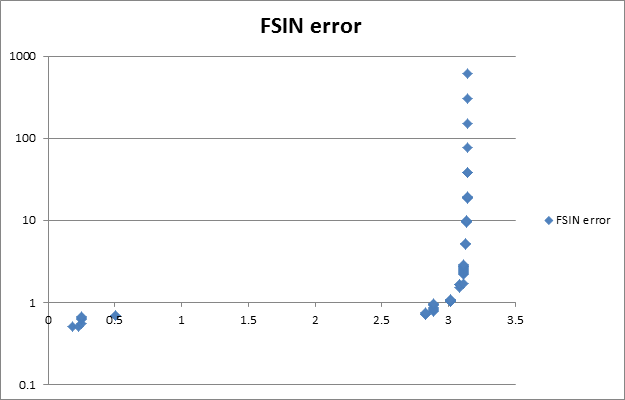fsin_error.png 1より

ハードウェア実装: CORDICアルゴリズム

x87 では CORDIC アルゴリズムというアルゴリズムが使用されている。
それについては、2 の資料に詳しく説明がある。

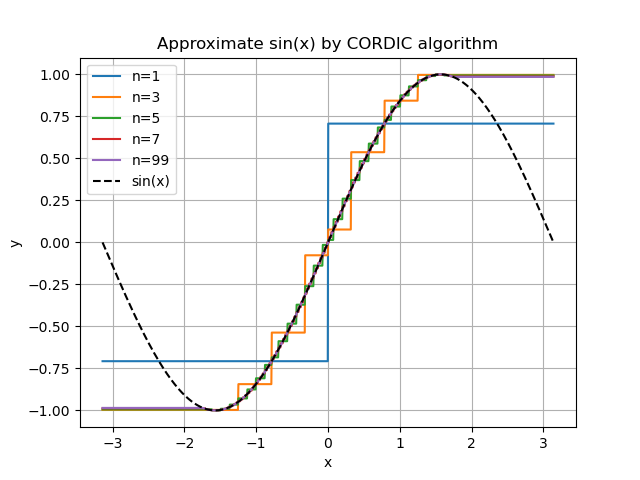
このアルゴリズムを python で実装し、sin関数を近似すると、以下のようになった。

Figure_1.png

ソフトウェア実装: テイラー展開(マクローリン展開)

最近のプログラミング言語の三角関数の実装には、概ねテイラー展開(マクローリン展開)を用いられるようである。

テイラー展開では、求めたい関数$f(x)$を、その$n$次微分関数$f^{(n)}{(x)}$ と定数 $a$ を用いて、次式で表すことができる。
(関数 $f$ の点 $a$ まわりのテイラー級数)

3

$a=0$ とすると、$\sin(x)$ の微分関数は $\cos(x)$, $-\sin(x)$, $-\cos(x)$, $\sin(x)$, ... となり、
$\cos(0)= 1$, $\sin(0)=0$ であるから、偶数番目の項だけ残り、最終的に次のようになる。

3

$\cos(x)$ も同じように簡単な形式で表すことができる。

実際にコンピュータで計算するときは、無限個の項を計算することは不可能なので、近似的に適当な項まで計算することになる。

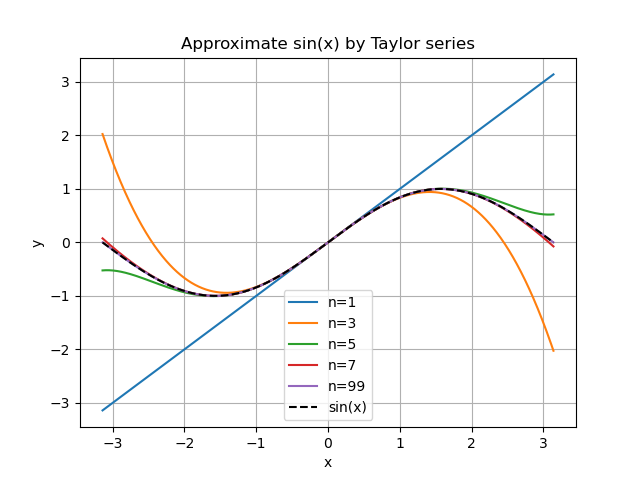
このアルゴリズムを python で実装し、sin関数を近似すると、以下のようになった。

Figure_2.png

付録: CORDIC アルゴリズムの実装

  • CORDIC アルゴリズムで近似した sin 関数をグラフに表示するプログラムです。
  • 実行には matplotlib および numpy が必要です。
import math

import matplotlib.pyplot as plt
import numpy as np


class CORDIC:
    def __init__(self, n: int) -> None:
        self.n = n
        self.theta = [math.atan2(1, math.pow(2, i)) for i in range(n)]

        w = 1.0
        h = 1.0
        for i in range(n):
            w = math.sqrt(math.pow(w, 2) + math.pow(h, 2))
            h = w * pow(0.5, i + 1)

        self.r = w

    def compute(self, theta: float) -> float:
        t = 0.0
        x = 1.0
        y = 0.0

        for i in range(self.n):
            if t < theta:
                t += self.theta[i]
                s = +1.0
            else:
                t -= self.theta[i]
                s = -1.0

            x_ = x
            y_ = y
            x = x_ - s * math.pow(0.5, i) * y_
            y = y_ + s * math.pow(0.5, i) * x_

        return x, y

    def approx_sin(self, theta: float) -> float:
        _, y = self.compute(theta)
        return y / self.r

    def approx_cos(self, theta: float) -> float:
        x, _ = self.compute(theta)
        return x / self.r

    def approx_tan(self, theta: float) -> float:
        x, y = self.compute(theta)
        return y / x


def main():
    cordic1 = CORDIC(n=1)
    cordic3 = CORDIC(n=3)
    cordic5 = CORDIC(n=5)
    cordic7 = CORDIC(n=7)
    cordic99 = CORDIC(n=99)

    x = np.linspace(-math.pi, math.pi, 1000)
    y = np.vectorize(math.sin)(x)
    y1 = np.vectorize(lambda x: cordic1.approx_sin(x))(x)
    y3 = np.vectorize(lambda x: cordic3.approx_sin(x))(x)
    y5 = np.vectorize(lambda x: cordic5.approx_sin(x))(x)
    y7 = np.vectorize(lambda x: cordic7.approx_sin(x))(x)
    y99 = np.vectorize(lambda x: cordic99.approx_sin(x))(x)

    plt.plot(x, y1, label="n=1")
    plt.plot(x, y3, label="n=3")
    plt.plot(x, y5, label="n=5")
    plt.plot(x, y7, label="n=7")
    plt.plot(x, y99, label="n=99")
    plt.plot(x, y, linestyle="dashed", color="black", label="sin(x)")

    plt.title("Approximate sin(x) by CORDIC algorithm")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid()
    plt.show()
    plt.close()


if __name__ == "__main__":
    main()

付録: テイラー展開を使用した近似sin関数の実装

  • テイラー展開で近似した sin 関数をグラフに表示するプログラムです。
  • 実行には matplotlib および numpy が必要です。
import math

import matplotlib.pyplot as plt
import numpy as np


def approx_sin(x: float, n: int):
    t = 0.0
    for i in range(1, n + 1, 2):
        s = +1.0 if (i - 1) % 4 == 0 else -1.0
        t += s * pow(x, i) / math.factorial(i)
    return t


def main():
    x = np.linspace(-math.pi, math.pi, 1000)
    y = np.vectorize(math.sin)(x)
    y1 = np.vectorize(lambda x: approx_sin(x, n=1))(x)
    y3 = np.vectorize(lambda x: approx_sin(x, n=3))(x)
    y5 = np.vectorize(lambda x: approx_sin(x, n=5))(x)
    y7 = np.vectorize(lambda x: approx_sin(x, n=7))(x)
    y99 = np.vectorize(lambda x: approx_sin(x, n=99))(x)

    plt.plot(x, y1, label="n=1")
    plt.plot(x, y3, label="n=3")
    plt.plot(x, y5, label="n=5")
    plt.plot(x, y7, label="n=7")
    plt.plot(x, y99, label="n=99")
    plt.plot(x, y, linestyle="dashed", color="black", label="sin(x)")

    plt.title("Approximate sin(x) by Taylor series")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid()
    plt.show()
    plt.close()


if __name__ == "__main__":
    main()

付録: x87 fsin と C++ 標準ライブラリの sin() の比較

説明
x87 fsin 命令と、C++ 標準ライブラリの sin 関数の計算結果を比較し、乖離があるか調べるプログラムです。

  1. 0 ~ M_PI までの範囲から、一様分布の確率分布で、疑似乱数 x を生成します。
  2. C++ 標準ライブラリの sin() で sin(x) の近似値を求めます。(y1)
  3. x87 fsin で sin(x) の近似値を求めます。(y2)
  4. 2 3 の計算結果に (大きな) 違いがある場合、コンソールに x y1 y1 y2 差 を表示します。
    • "差" はメモリのビットレベルでの差です。(reinterpret_cast<const int64_t&>(y1) - reinterpret_cast<const int64_t&>(y2))
  5. 1 - 4 を N(=1000000) 回繰り返します。

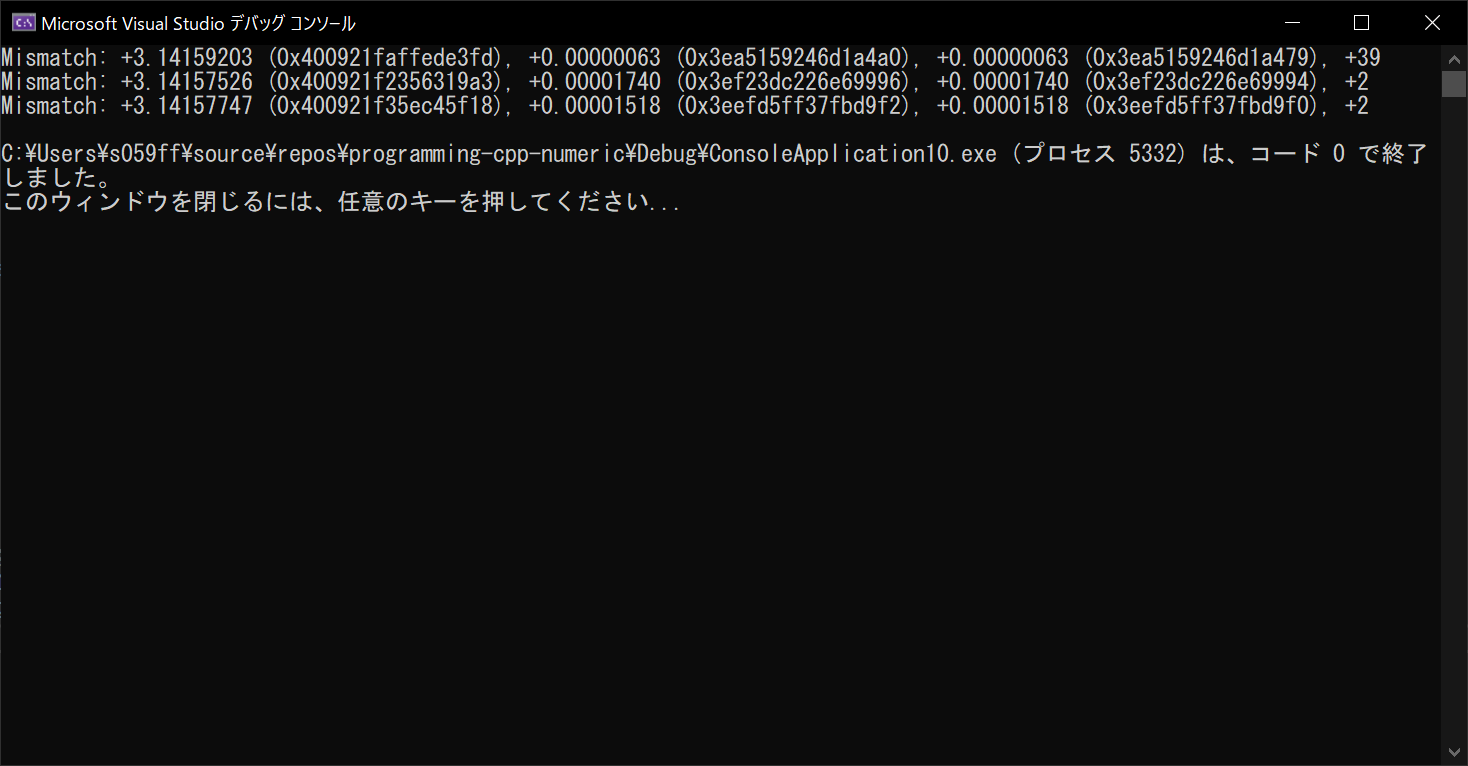
実行結果

  • Windows 10 Pro 64bit
  • AMD Ryzen 7 3700X プロセッサー (Intel CPU など他の CPU では実行結果が多少変わるかもしれません。)

stdsin_vs_fsin.png

ソースコード

※Visual Studio 2022 でビルド、動作。ターゲットプラットフォームを x86 にすること。(x64 ではビルドエラー)

#define _USE_MATH_DEFINES

#include <algorithm>
#include <cmath>
#include <iostream>
#include <iomanip>
#include <numeric>
#include <random>
#include <vector>

using F = double;
using I = int64_t;

static_assert(sizeof(F) == sizeof(I), "");

constexpr size_t N = 1000000;
constexpr unsigned int S = 12345;

int main()
{
    std::default_random_engine engine(S);
    std::uniform_real_distribution<F> dist(0, static_cast<F>(M_PI));

    std::cout
        << std::fixed
        << std::setprecision(8)
        << std::showbase
        << std::showpos;

    F x = 0;
    F y1 = 0, y2 = 0;
    const I& x_i = reinterpret_cast<const I&>(x);
    const I& y1_i = reinterpret_cast<const I&>(y1);
    const I& y2_i = reinterpret_cast<const I&>(y2);

    for (size_t i = 0; i < N; i++)
    {
        x = dist(engine);
        y1 = sin(x);

        __asm {
            fld x
            fsin
            fstp y2
        }

        auto diff = y1_i - y2_i;

        if (1 < abs(diff))
        {
            std::cout << "Mismatch: "
                << x << " " << "(" << std::hex << x_i << ")" << ", "
                << y1 << " " << "(" << std::hex << y1_i << ")" << ", "
                << y2 << " " << "(" << std::hex << y2_i << ")" << ", "
                << std::dec << diff << std::endl;
        }
    }
}

1 で説明されていたように、$x\approx\pi$ の場合、正確な値から大きく乖離してしまうようです。

  1. https://www.intel.com/content/dam/develop/external/us/en/documents/x87trigonometricinstructionsvsmathfunctions.pdf, "The Difference Between x87 Instructions FSIN, FCOS, FSINCOS, and FPTAN and Mathematical Functions sin, cos, sincos, and tan" ↩ ↩2 ↩3 ↩4

  2. https://teamcoil.sp.u-tokai.ac.jp/calculators/column/100224/index.html, "「サルでも分かるCORDICアルゴリズム」" ↩

  3. https://ja.wikipedia.org/wiki/%E3%83%86%E3%82%A4%E3%83%A9%E3%83%BC%E5%B1%95%E9%96%8B, "テイラー展開" ↩ ↩2

15
13
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
15
13