はじめに
千葉大学/Nospareの米倉です.今回は最近ちょっと話題になった,「ガウス・マルコフの定理」についての解説と,Juliaを用いた簡単な数値実験を紹介したいと思います.
設定
定理の内容を解説する前に,問題の設定をまず述べます.$\mathbf{y}$を$n$次元の被説明変数,$\mathbf{X}$を$n\times p$の説明変数の行列,$\beta$を$p$次元のベクトルとして,回帰モデル$\mathbf{y}=\mathbf{X}\beta+\epsilon$を考えます.$\epsilon$は$\mathbb{E}[\epsilon]=0$,$\mathrm{Cov}[\epsilon]=\sigma^{2}\mathbf{I}$をみたす,$n$次元の確率ベクトルです.ここで,$\mathbf{I}$は$n$次元の単位行列です.
この時,最小二乗推定量(OLSE)はある仮定の下で$\hat\beta_{OLSE}=(\mathbf{XX^{\top}})^{-1}\mathbf{X^{\top}y}$となり,その分散は,$\mathrm{Var}[\hat\beta_{OLSE}]=\sigma^2(\mathbf{X}^{\top}\mathbf{X})^{-1}$と計算できます.また$\mathbb{E}[\hat\beta_{OLSE}]=\beta$も成立し,OLSEは不偏推定量です.
ガウス・マルコフの定理が述べているのは,任意の不偏かつ線形な推定量の中で,OLSEの分散が最小になるということです.これをもって,OLSEは best linear unbiased estimator (BLUE)と言われます.証明についてはネットで検索するといくつか見つけられるのでそちらを参照してみてください.
数値実験
ガウス・マルコフの定理の意味を視覚的に理解するために次の様な実験をしてみました.
今$n=21$とし,$\beta=[1.0,2.0]^\top$と真値を定めます.また$\mathbf{X}$の1列目は全て1,2列目は標準正規分布から21個乱数を発生させて格納し,$\mathbf{y}=\mathbf{X}\beta+\epsilon$とデータ$\mathbf{y}$を作りました.ここで,$\epsilon\sim\mathcal{N}(0,2\mathbf{I})$です.$\mathbf{X}$は固定し,$\epsilon$を10,000回独立に発生させることによって,サンプルサイズ21のデータセットを10,000個作成しました.
このデータに対して,推定方法を2つ考えます.まずは普通のOLS推定です.次に,21個のデータを3等分しそれぞれでOLS推定を行い,最後にその平均を取るという推定方法を考えました.これも不偏推定量であることがわかり,分割推定量と呼ぶことにします.
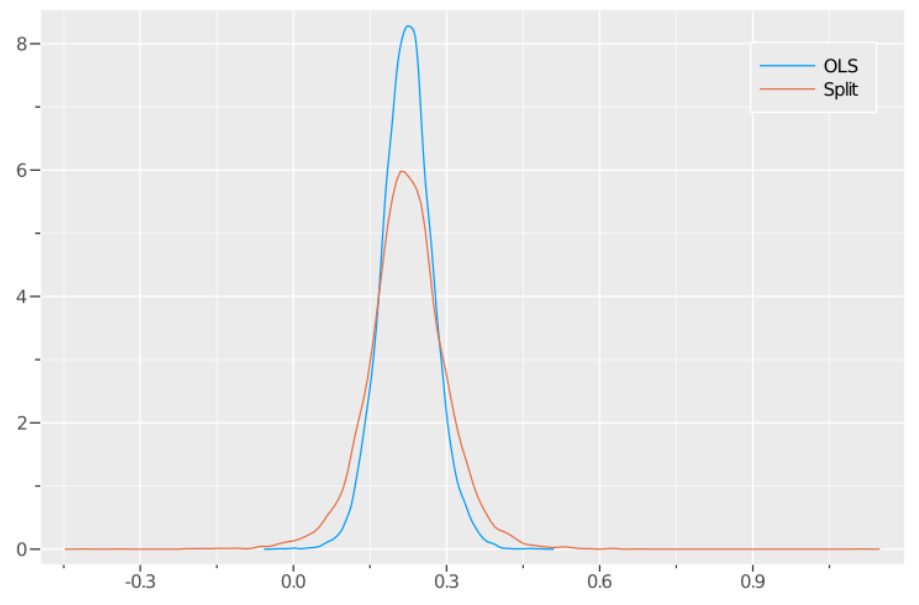
次の図は以上の手続きで求めた10,000個の$\beta=2$に対する推定値を元にして,その密度をプロットしたものです.青い線がOLSE,オレンジの線が分割推定量の結果です.まず二つともバイアスが無いことが分かります.一方で,OLSEの方が分割推定量よりも密度関数の裾が小さい(分散が小さい)ことが分かると思います.これがガウス・マルコフ定理が述べていることです.参考までに,Juliaのコードを載せておきます.
using Plots
using Statistics
using StatsPlots
theme(:ggplot2)
reps = 10000
n = 21
sig = 2.0
x = [ones(n,1) randn(n,1)]
beta = [1.0, 2.0]
Pop = x*beta
estimate = zeros(reps,2)
for i = 1:reps
e = sig*randn(n)
y = Pop + e
# OLSE
estimate[i,1] = (y\x)[2]
# average of split estimator
y1 = y[1:7,:]
y2 = y[8:14,:]
y3 = y[15:21,:]
x1 = x[1:7,:]
x2 = x[8:14,:]
x3 = x[15:21,:]
beta_ss1 = y1\x1
beta_ss2 = y2\x2
beta_ss3 = y3\x3
beta_ss = (beta_ss1 + beta_ss3 + beta_ss3)/3.0 # average
estimate[i,2] = beta_ss[2]
end
density(estimate[:,1],lab="OLS")
density!(estimate[:,2],lab="Split")
最近話題になったこと
OLSEは「不偏」で「線形な」推定量の中で分散が最小になりますが,最近Bruce E. Hansen, A Modern Gauss-Markov Theorem.で「線形」が外せることが示されました.つまり,線形とは限らないより広い不偏推定量のクラスの中でOLSEの分散は最小になることを意味しています.これは教科書の内容を書き換える必要がある中々凄い結果だと思います.なのでBLUEではなく,BUEになってしまい,どう発音するかまだ定まってません.ブゥとかだとカッコ悪いですね.
終わりに
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.
