SciPyのMILPは使えるのか？？（SciPy==1.9.0の新機能の検証）

モチベーション

2022/07/29に以下図にある通り、SciPy==1.9.0がリリースされてMILPの機能が追加された。
MILPを実務で活用する場合、求解速度の観点からGurobiやCPLEXがを利用するのが一般的である。
しかし、これらの有償ソルバーは高額であり、手軽に活用することはできない。
Gurobiの機能と比較し、SciPyのMILPソルバーが実務適用可能なレベルの性能を備えているか調査した。

https://docs.scipy.org/doc/scipy-1.9.0/release.1.9.0.html

調査結果

1. 表現できるMILPが限定的であり、複雑な実務での定式化を行うことは難しい

基本的に、以下数式で表現される定式化しか解くことができない。
もっとも致命的なのが、決定変数(x)が1次元しか取ることができない。
容器が複数の場合のナップザック問題すら解くことができない。

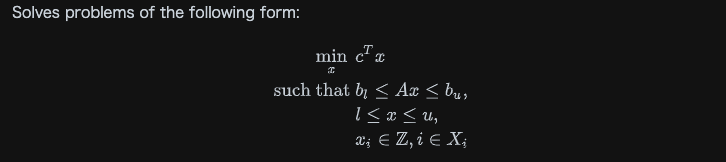
https://docs.scipy.org/doc/scipy-1.9.0/reference/generated/scipy.optimize.milp.html#scipy.optimize.milp

2. 表現は限定されているものの、求解速度はGurobiに匹敵する

ナップザック問題のitem数を100万とした場合の次のソースコードを実行し、各ソルバーの性能を調べた。
結果はそれぞれ次のようになった。（モデリングにかかる時間は除き、milpを解く時間のみ測定）

• SciPy: 57.9s
• Gurobi: 35.4s
• glpk: 終わらない

100万の規模は無償ソルバーでは解けないため、この結果には少々驚いた。
表現が限定的ではあるが活用先はあるかもしれない。

import numpy as np
import random
import time
import pyomo.environ as pyo
from scipy.optimize import milp
from scipy.optimize import LinearConstraint, Bounds

class KnapsackProblem:
    item_num=1000000
    seed=12345
    
    def __init__(self):
        random.seed(self.seed)
        self.item_id_list = [i for i in range(self.item_num)]
        self.weight_list = [random.randint(1, 10) for _ in range(self.item_num)]
        self.value_list = [random.randint(1, 10) for _ in range(self.item_num)]
        self.knapsack_capacity = int(np.sum(self.weight_list)/2)
        return None

def create_knapsack_model_by_pyomo():
    p = KnapsackProblem()
    
    mdl = pyo.ConcreteModel()
    
    # パラメタ定義
    mdl.N = pyo.Set(initialize=p.item_id_list)
    mdl.w = pyo.Param(mdl.N, initialize=dict(zip(p.item_id_list, p.weight_list)))
    mdl.v = pyo.Param(mdl.N, initialize=dict(zip(p.item_id_list, p.value_list)))
    mdl.c = pyo.Param(initialize=p.knapsack_capacity)
    
    # 決定変数
    mdl.X = pyo.Var(mdl.N, within=pyo.Binary)
    
    # 目的関数定義
    def obj(mdl):
        return sum(mdl.v[i]*mdl.X[i] for i in mdl.N)
    
    mdl.obj = pyo.Objective(rule=obj, sense=pyo.maximize)
    
    # 制約条件定義
    def const(mdl):
        return sum(mdl.w[i]*mdl.X[i] for i in mdl.N) <= mdl.c
    
    mdl.const = pyo.Constraint(rule=const)
        
    return mdl

def time_printer(time):
    print("====================================")
    print(f"{round(time, 1)}s")
    print("====================================")
    print("\n\n")
    return None
    
def solve_ksp_by_pyomo(solver):
    mdl = create_knapsack_model_by_pyomo()
    opt = pyo.SolverFactory(solver)
    
    
    print(f"solving by {solver}...")
    time_start = time.time()
    res = opt.solve(mdl, tee=False)
    time_finish = time.time() - time_start
    
    print(res)
    time_printer(time_finish)
    
    return None
    

def solve_ksp_by_scipy():
    
    p = KnapsackProblem()
    c = -np.array(p.value_list)
    A = np.array([p.weight_list])
    b_u = np.array([p.knapsack_capacity])
    b_l = np.array([0])
    integrality = np.ones_like(c)

    print("solving by scipy...")
    time_start = time.time()
    res = milp(c=c,
        constraints=LinearConstraint(A, b_l, b_u), 
        bounds=Bounds(lb=0, ub=1),
        integrality=integrality,
    )
    time_finish = time.time() - time_start
    
    print(res)
    time_printer(time_finish)
    
    return None


if __name__ == "__main__":
    solve_ksp_by_pyomo("gurobi") # 35.4s
    solve_ksp_by_scipy() # 57.9s

結論

実務MILPを解く場合は、GurobiやCPLEXを使うしかない。