概要
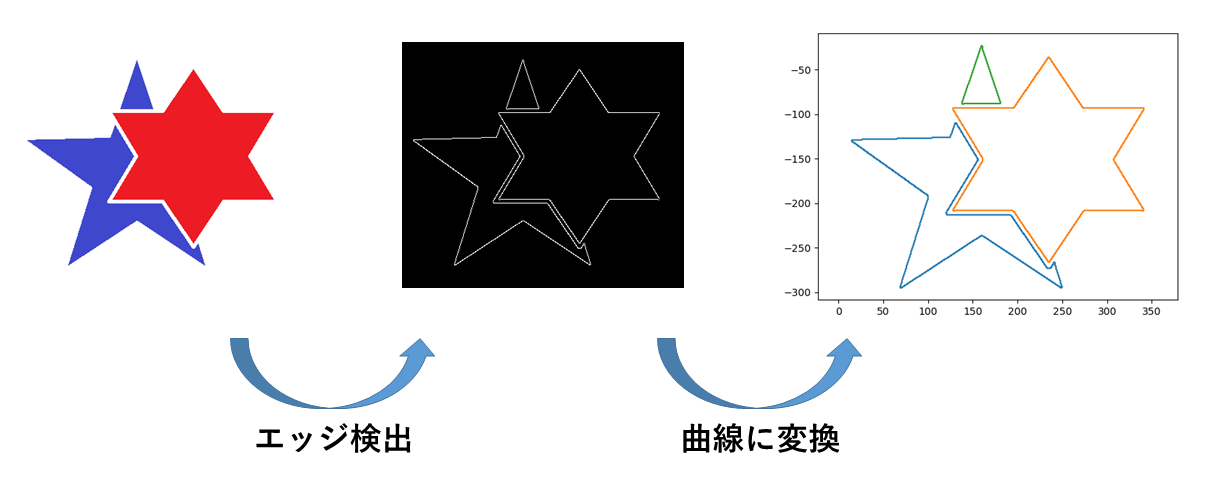
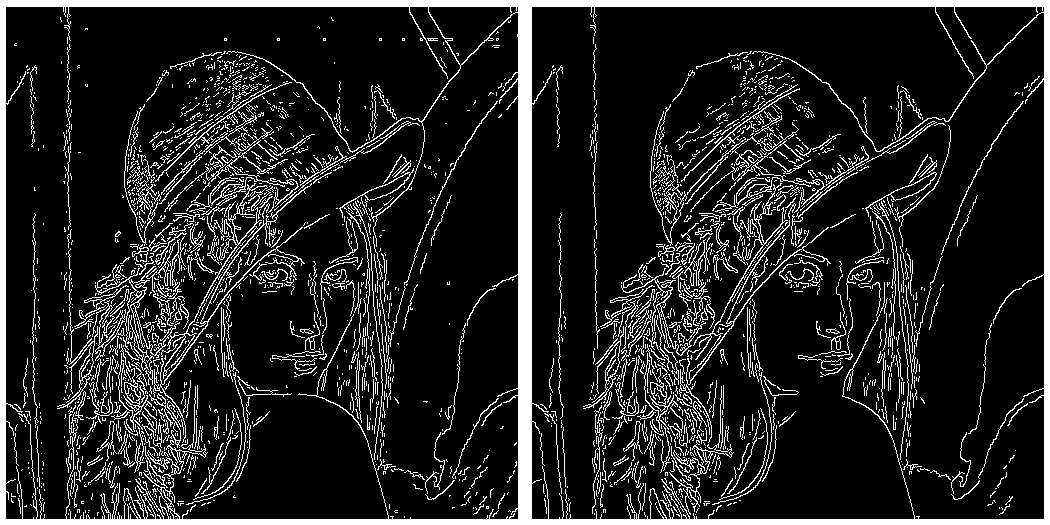
OpenCVのcv2.Canny()関数に画像を投げると上図中央のようなエッジ検出結果が返されるが,このままだとエッジはただの白点の集合であり扱いづらい.そこで,エッジ検出結果のエッジを表す白点を繋いでいき,『いい感じ』の曲線(折れ線)を生成することを目指す.折れ線に変換することで,例えばBスプライン曲線補完することでエッジの連続化とスムージングを行ったり,閉じたエッジの場合は囲まれた部分の面積を求めたりできるようになる.最も素朴な方法は一番近い点同士をを繋いでいくというもので,この方法でも割といい感じの折れ線にはなるが,ここではもう少し工夫を凝らす.
表記に関する注釈
- $\left(a_1, \dots, a_N \right)$ のように丸括弧で表記されたものは順列を表す.
- $\left\{a_1, \dots, a_N \right\}$ のように波括弧で表記されたものは集合を表す.
- $\left[a_1, \dots, a_N \right]$ のように角括弧で表記されたものはベクトルを表す.
- $\|\cdot\|$ はユークリッドノルムを表す.
手順
エッジを構成する点(画素)を__エッジ点__と呼ぶことにする.また,エッジ点はエッジ点への位置ベクトルとして表現する.
折れ線はエッジ点 $\boldsymbol{p}_i$ の順列
l = \left( \boldsymbol{p}_1, \dots, \boldsymbol{p}_N \right), \quad \boldsymbol{p}_i = \left[ x_i, y_i \right]^\mathrm{T}
として表現でき,これを作成する.エッジは複数の折れ線に変換されるときもあり,このときは $l_1, l_2, \dots$ を作成することになる.折れ線作成の手順は次の通り:
- 画像を
cv2.Canny()に投げてエッジ検出を行い,エッジを構成するすべてのエッジ点を格納した集合 $P$ を用意する. - $i = 1$とする.
- 空の順列 $l_i$ を用意する.
- エッジ点の集合 $P$ からランダムで1点選んで $l_i$ に追加し $P$ から取り除く.
- $l_i$ の__最後尾__のエッジ点 $\boldsymbol{p}_\mathrm{tail}$ の近傍で目的関数(後述)を最小にするエッジ点 $\boldsymbol{p} \in P$ を探して $l_i$ 最後尾に追加し $P$ から取り除く.
- $\boldsymbol{p}_\mathrm{tail}$ の近傍にエッジ点が見つからなくなるか,目的関数の最小値が予め設定した閾値を超えるまで5.を繰り返す.
- $l_i$ の順序を反転させてもう一度5.と6.を実行する.
- $P$ にエッジ点が残ってる場合は $i \leftarrow i+1$ として3.に戻る.
具体的な説明
上の手順をもう少し詳しく見ていく.
手順1.
OpenCVのcv2.Canny()関数に画像を投げると次のような行列が返ってくる(画像が5×5の場合の例):
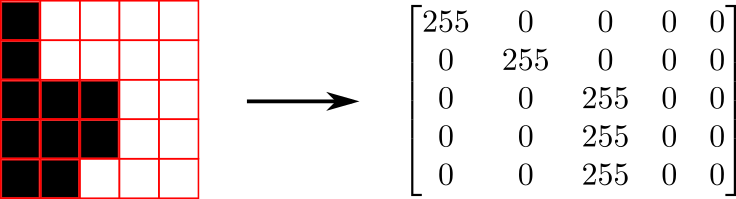
行列の255の位置が画像におけるエッジ点の位置に対応する.画像に対して適当に$x$軸と$y$軸を定め,エッジを構成するすべてのエッジ点の位置ベクトル $\boldsymbol{p}$ を集めた集合 $P$ を作る.座標の取り方は任意だが行列の $(i, j)$-成分が表す点の位置を $[x, y]^\mathrm{T} = [j, -i]^\mathrm{T}$ とするのがいいだろう.こうすると,折れ線をmatplotlib.pyplot.plot()で表示したときの向きが画像の向きと一致する.
手順5~6.
$P$ に含まれるエッジ点のうち,あるエッジ点 $\boldsymbol{p}'$ から距離 $d$ 以内にあるものの集合を $P_\mathrm{n} \left( \boldsymbol{p}', d \right)$と書くことにする.すなわち,
P_n \left( \boldsymbol{p}', d \right) := \left\{ \boldsymbol{p} \in P : \| \boldsymbol{p} - \boldsymbol{p}'\| \le d \right\}
手順5.では,エッジ点の順列 $l_i$ の最後尾のエッジ点を $\boldsymbol{p}_\mathrm{tail}$ ,『近傍』とみなす距離の閾値を $\theta_{\mathrm{n}}$ として $P_\mathrm{n} \left( \boldsymbol{p}_\mathrm{tail}, \theta_\mathrm{n} \right)$ を求め,空集合でなければ各エッジ点の候補 $\boldsymbol{p} \in P_\mathrm{n} \left( \boldsymbol{p}_\mathrm{tail}, \theta_\mathrm{n} \right)$ について目的関数(後述)を計算する.目的関数の最小値が予め設定した閾値 $\theta_\mathrm{c}$ を超えなければ,目的関数を最小化する $\boldsymbol{p}$ を $l_i$ の最後尾に加え, $P$ から取り除く.
この操作を $P_\mathrm{n} \left( \boldsymbol{p}_\mathrm{tail}, \theta_\mathrm{n} \right)$ が空集合になるか,目的関数の最小値が $\theta_\mathrm{c}$ を超えるまで繰り返す.目的関数は折れ線が『いい感じ』になるようなエッジ点 $\boldsymbol{p}$ で最小になるように設計されているため,このようにすることで折れ線が『良い感じ』になるように紡がれていく.
NOTE: $\theta_\mathrm{n}$ と $\theta_\mathrm{c}$ は予め定めておくパラメータである.
手順8.
$P$ にエッジ点が残っていれば次の折れ線 $l_{i+1}$ の作成のために手順3.に戻り,残っていなければ終了する.
目的関数
いままで『いい感じ』というワードを使ってきたが,どのような折れ線が『いい感じ』であるといえるかは状況によって異なる.ただ単に最も近いエッジ点を結んでいくだけでいいのなら折れ線の端との距離を目的関数にすれば良いし,「あまりくねくねした折れ線にはなってほしくない」という要請があれば折れ線が曲がってしまう場合に値が大きくなるような関数を目的関数にすればいい.
ここでは最も多いであろう「できるだけ近い点同士をつなげてほしいが,あまりくねくねした折れ線にはなってほしくない」という要請を満たす目的関数の例を示す.
現在の折れ線が $l = \left( \boldsymbol{p}_1, \dots, \boldsymbol{p}_N \right)$ であるとして,$\boldsymbol{r}$ を折れ線の最後尾( $\boldsymbol{p}_N$ )から折れ線に新たに加えるエッジ点の候補 $\boldsymbol{p}$ に向かうベクトル,すなわち
\boldsymbol{r} := \boldsymbol{p} - \boldsymbol{p}_N
で定義し,$N \ge 3$ のときは単位ベクトル $\boldsymbol{\hat{d}}$ を
\boldsymbol{d} = \left( \boldsymbol{p}_N - \boldsymbol{p}_{N-1} \right) + k \left( \boldsymbol{p}_{N-1} - \boldsymbol{p}_{N-2} \right) \\
\boldsymbol{\hat{d}} := \frac{\boldsymbol{d}}{\|\boldsymbol{d}\|}
で定義する.ただし,$k \in [0,1]$ は予め与えるパラメータである.$k = 0.5$ のときの例は下の図の通り.
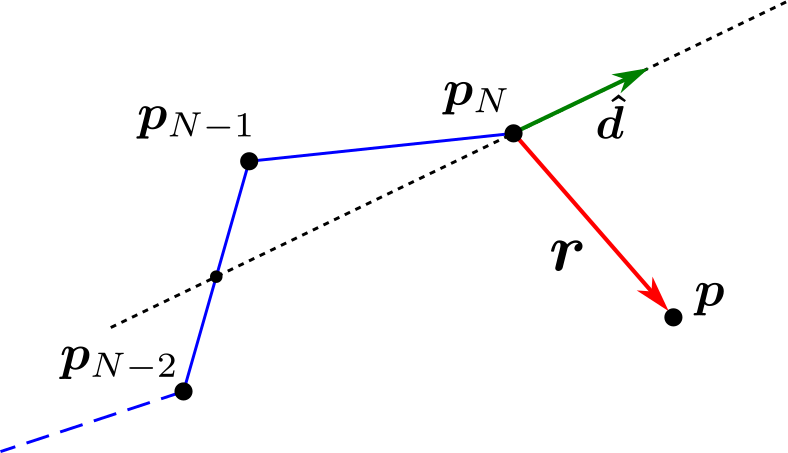
NOTE:$k = 0.5$ とすると $\boldsymbol{d} = \boldsymbol{0}$ となって単位ベクトル $\boldsymbol{\hat{d}}$ が求められなくなる場合が発生しやすいので,実装の際は $k = 0.47$ のように少しずらしておく方が良い.
そして,目的関数を
J := \begin{cases}
\|\boldsymbol{r}\|^2 & \left( N = 1, 2 \right) \\
\|\boldsymbol{r}\|^2 - \eta \left( \boldsymbol{r} \cdot \boldsymbol{\hat{d}} \right) & \left( N \ge 3 \right)
\end{cases}
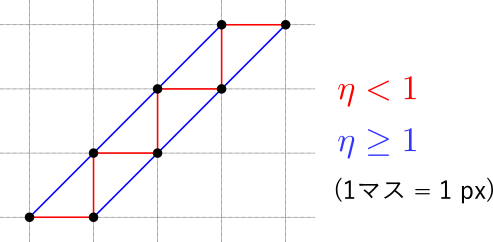
と定義して完成である.ただし,$\eta \ge 0$ は予め与えるパラメータである.第一項は「できるだけ近い点が良い」という要請に対応し,第二項が「曲がってほしくない」という要請に対応する.$\eta$ を大きくすればするほど折れ線は曲がらなくなるが,$\eta$ に1以上の値を設定すると階段状に分布したエッジ点を下の図のように繋いでしまい,本来1本であったエッジを2本折れ線に変換してしまうため,ほとんどの場合では $\eta$ は1未満にしておくのが良いと思われる.
実装例1
上で説明した手順の素朴な実装例を下に示す.edges2polylines()関数が本体である.ただし,目的関数は折れ線の最後尾との距離,すなわち
J := \|\boldsymbol{r}\|
とした.
import random
import math
import numpy as np
def edges2polylines(edges, th_n=6, th_c=None):
"""
cv2.Canny()から返されるエッジ検出結果からエッジ点を読みより折れ線に変換する
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
th_n : int or float
近傍とみなす点の距離の閾値
th_c : int or float
許容する目的関数の最小値の閾値
Returns
-------
polylines : list of list of numpy.ndarray
折れ線のリスト[l1, l2, ... ]
"""
th_c = th_c or th_n
edgepoints = get_edgepoints(edges) # エッジ点の集合 P
polylines = [] # 折れ線 l1, l2, ... を格納するリスト
while edgepoints:
n_edgepoints = len(edgepoints)
init_idx = random.randrange(n_edgepoints)
polyline = [] # 折れ線 li (手順3.)
polyline.append(edgepoints.pop(init_idx)) # 手順4.
could_reverse = True
while True:
# 折れ線の最後尾の近傍にあるエッジ点を取得する
indices = range(len(edgepoints))
nearest = filter(lambda i: distance(edgepoints[i], polyline[-1]) <= th_n, indices)
nearest = sorted(nearest, key=lambda i: distance(edgepoints[i], polyline[-1]))
# 近傍にエッジ点がなかった時の処理
if not nearest:
if could_reverse:
polyline.reverse()
could_reverse = False
continue
else:
break
# 目的関数(cost_function())を小さくする順に並び替え
nearest = sorted(nearest, key=lambda i: cost_function(edgepoints[i], polyline[-1]))
# 目的関数の最小値が閾値を超えていた時の処理
if cost_function(edgepoints[nearest[0]], polyline[-1]) > th_c:
if not nearest:
if could_reverse:
polyline.reverse()
could_reverse = False
continue
else:
break
# 目的関数を最小にするものを折れ線の最後尾に追加し,P からその点を削除する
polyline.append(edgepoints.pop(nearest[0]))
# 折れ線 li を折れ線のリストに追加する
polylines.append(polyline)
return polylines
def cost_function(p, line_end):
"""
目的関数
Parameters
----------
p : numpy.ndarray
エッジ点
line_end : numpy.ndarray
折れ線の末端のエッジ点
Returns
-------
res : float
目的関数の評価値
"""
res = distance(p, line_end)
return res
def get_edgepoints(edges):
"""
cv2.Canny()から返されるエッジ検出結果からエッジ点の位置を取得する
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
Returns
-------
edgepoints : list of numpy.ndarray
エッジ点の位置のリスト
[[x1,y1], [x2,y2], ... ]
"""
il, jl = np.where(edges == 255)
edgepoints = [np.array([j, -i]) for i, j in zip(il, jl)] # エッジ点の集合 P
return edgepoints
def distance(a, b):
"""
2点間のユークリッド距離を求める(2次元)
Parameters
----------
a : array-like
点1
b : array-like
点2
Returns
-------
d : float
二点間のユークリッド距離
"""
d = math.sqrt((a[0] - b[0]) ** 2 +
(a[1] - b[1]) ** 2)
return d
実装例2
実装例1は遅いのですこし改善した実装例を下に示す.edges2polylines()関数が本体である.ただし,目的関数には上で提案した「できるだけ近い点同士をつなげてほしいが,あまりくねくねした折れ線にはなってほしくない」という要請を満たす目的関数
J := \begin{cases}
\|\boldsymbol{r}\|^2 & \left( N = 1, 2 \right) \\
\|\boldsymbol{r}\|^2 - \eta \left( \boldsymbol{r} \cdot \boldsymbol{\hat{d}} \right) & \left( N \ge 3 \right)
\end{cases}
を採用した.
import random
import math
import numpy as np
def edges2polylines(edges, th_n=6, th_c=None):
"""
cv2.Canny()から返されるエッジ検出結果からエッジ点を読みより折れ線に変換する
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
th_n : int or float
近傍とみなす点の距離の閾値
th_c : int or float
許容する目的関数の最小値の閾値
Returns
-------
polylines : list of list of numpy.ndarray
折れ線のリスト[l1, l2, ... ]
"""
edges_tmp = edges.copy()
th_c = th_c or th_n ** 2
edgepoints = get_edgepoints(edges_tmp) # エッジ点の集合 P
init_n_points = len(edgepoints)
polylines = [] # 折れ線 l1, l2, ... を格納するリスト
count = 0
while count < init_n_points:
edgepoints = get_edgepoints(edges_tmp)
n_points = len(edgepoints)
init_idx = random.randrange(n_points)
polyline = [] # 折れ線 li
polyline.append(convert_imshow2plot(edgepoints[init_idx]))
delete_edges(edges_tmp, edgepoints[init_idx])
count += 1
could_reverse = True
while True:
# 折れ線の最後尾の近傍にあるエッジ点を取得する
nearest = search_neighbor_points(edges_tmp, polyline[-1], th_n)
# 線の端に近い順に並び替え
nearest = sorted(nearest, key=lambda p: distance(p, polyline[-1]))
# 近傍にエッジ点がなかった時の処理
if not nearest:
if could_reverse:
polyline.reverse()
could_reverse = False
continue
else:
# 近くに点もなく,既に反転済みのときは線の作成を終える
break
if len(polyline) <= 2:
next_point = nearest[0]
else:
# line[-2]とline[-3]の中点からline[-1]へ向かうベクトル
d = (polyline[-1] - polyline[-2]) + 0.47 * (polyline[-2] - polyline[-3])
d = d / np.linalg.norm(d) # 正規化
nearest = sorted(nearest, key=lambda p: cost_function(p, polyline[-1], d))
# 目的関数の最小値が閾値を超えていた時の処理
if cost_function(nearest[0], polyline[-1], d) > th_c:
if could_reverse:
polyline.reverse()
could_reverse = False
continue
else:
break
next_point = nearest[0]
polyline.append(next_point)
delete_edges(edges_tmp, convert_plot2imshow(next_point))
count += 1
polylines.append(polyline)
return polylines
def cost_function(p, line_end, d):
"""
目的関数
Parameters
----------
p : numpy.ndarray
エッジ点
line_end : numpy.ndarray
折れ線の末端のエッジ点
d : numpy.ndarray
曲がり具合を計算するために用いる単位ベクトル
Returns
-------
res : float
目的関数の評価値
"""
r = p - line_end
r_norm = math.sqrt(np.dot(r, r))
res = r_norm ** 2 - 0.99 * np.dot(r, d)
return res
def search_neighbor_points(edges, a, th_c):
"""
edgesの中から点aからth_c以内の距離にある点を抽出する
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
a : numpy.ndarray
点
th_c : int or float
近傍と見なす距離の閾値
Returns
-------
neighbor_points : list of numpy.ndarray
aの近傍にある点のリスト
"""
neighbor_points = []
pl = points_inside_circle(a, th_c)
for p in pl:
p_img = convert_plot2imshow(p)
if p_img[0] < 0 or p_img[1] < 0:
continue
try:
if edges[p_img[0], p_img[1]] == 255:
neighbor_points.append(p)
except IndexError:
continue
return neighbor_points
def distance(a, b):
"""
2点間のユークリッド距離を求める(2次元)
Parameters
----------
a : array-like
点1
b : array-like
点2
Returns
-------
d : float
二点間のユークリッド距離
"""
d = math.sqrt((a[0] - b[0]) ** 2 +
(a[1] - b[1]) ** 2)
return d
def get_edgepoints(edges):
"""
cv2.Canny()から返されるエッジ検出結果からエッジ点の位置を取得する
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
Returns
-------
edgepoints : list of numpy.ndarray
エッジ点の位置のリスト
[[x1,y1], [x2,y2], ... ]
"""
il, jl = np.where(edges == 255)
edgepoints = [np.array([i, j]) for i, j in zip(il, jl)] # エッジ点の集合 P
return edgepoints
def points_inside_circle(center, r):
"""
centerを中心とする半径rの円の内部または円周上にある格子点のリストを返す
Parameters
----------
center : numpy.ndarray
円の中心
r : int or float
円の半径
Returns
-------
pl : list of numpy.ndarray
円の内部または円周上にある格子点のリスト
"""
pl = []
ri = math.floor(r)
xl = np.arange(-ri, ri + 1)
for x in xl:
y = math.sqrt(r ** 2 - x ** 2)
yi = math.floor(y)
yl = np.arange(-yi, yi + 1)
pl.extend([np.array([x, y]) + center for y in yl])
return pl
def delete_edges(edges, p):
"""
edgesの指定された点を0にする
Parameters
----------
edges : numpy.ndarray
cv2.Canny()から返されるエッジ検出結果
p : numpy.ndarray
0にする点(インデックス)
"""
edges[p[0], p[1]] = 0
def convert_imshow2plot(p):
"""
点pの座標系をimshowの座標系からplotの座標系へ変換する
Parameters
----------
p : numpy.ndarray
座標系を変換する点
Returns
-------
tmp : numpy.ndarray
変換済みの点p
"""
tmp = p.copy()
tmp[0] = p[1]
tmp[1] = - p[0]
return tmp
def convert_plot2imshow(p):
"""
点pの座標系をplotの座標系からimshowの座標系へ変換する
Parameters
----------
p : numpy.ndarray
座標系を変換する点
Returns
-------
tmp : numpy.ndarray
変換済みの点p
"""
tmp = p.copy()
tmp[0] = - p[1]
tmp[1] = p[0]
tmp = tmp.astype(np.int64)
return tmp
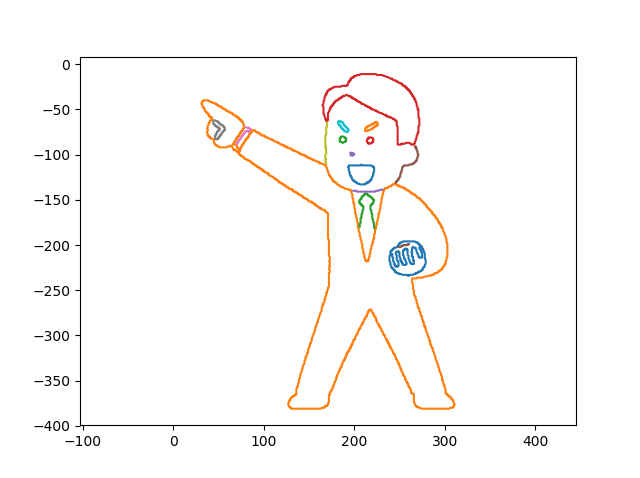
実行例
応用
閉じたエッジに囲まれた部分の面積を求める
閉じた折れ線は多角形であり,頂点の座標が時計回りまたは反時計回りに $(x_1,y_1), (x_2,y_2), \dots, (x_N,y_N)$ である多角形の面積は
S = \frac{1}{2} \left| \sum_{i=1}^{N} \left( x_{i}y_{i+1} - x_{i+1}y_{i} \right) \right|
で求められる.ただし,$(x_{N+1},y_{N+1}) = (x_1,y_1)$ .
ここで紹介した方法では折れ線は閉じられないため,折れ線の最後尾に折れ線の先頭の点を追加することで折れ線を閉じる必要がある.
ノイズの除去
エッジを折れ線に変換し,極端に短い折れ線をフィルタリングすることでエッジ検出結果からノイズを除去できる.