はじめに
この記事では、SVM(サポートベクタマシン)について、どのように実装をしているかを掲載しています。「SVMってなんだろう?」、「なんとなくやってることはわかるけど、マージン最大化とか識別境界って実際どうやって求めているんだろう?」という方はぜひ最後まで見ていただければと思います。
SVM(サポートベクタマシン)とは
SVMは、下のような2クラス分類問題を解く、線形識別器です(線形識別が何かは後述)。
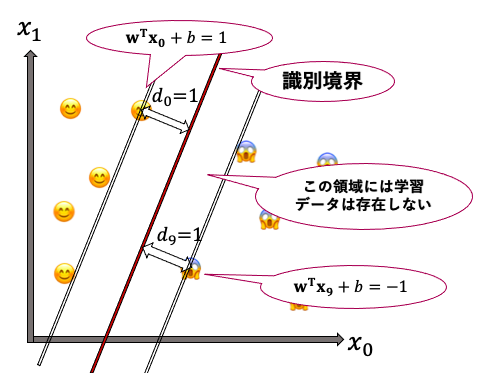
具体的には下のように😊 と😱 を分類したい場合に、右図の赤線のような「識別境界」を引くことを行います。この「識別境界」は「n次元特徴空間における, n-1次元特徴空間(超平面と呼ばれます)」となります。つまり、図のような2次元平面での場合は1次元である直線の識別境界が引かれ、3次元空間の場合は2次元平面の識別境界が生成されます。
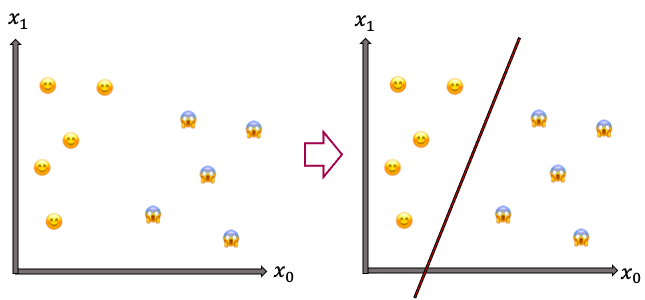
しかしこの例では、左下の図のように、引こうと思えば無限に識別境界を引くことができます。そこでSVMでは、識別境界から最も近い点(サポートベクタ)が識別境界から最も遠くなるように(余裕をもって分離できるように)、つまり、「サポートベクタから識別境界までの距離dが最大となるような超平面」を、識別境界とします(マージン最大化といいます)。
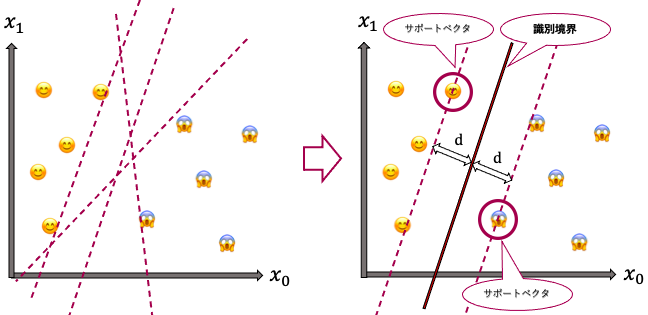
このように、学習データについて識別境界を引くことで、推定段階において、ある入力特徴量がどちらのクラスに属するのかを分類することができます。
じゃあ、そのマージン最大化した識別境界ってどうだしてるの??
ここまでの内容は知っているという方は多いと思いますが、「じゃあ実際にどのように識別境界を出しているのか」を知っている方はあまり多くはないのではないでしょうか。
ここからは、SVMの識別境界を求める手法について、ご紹介します。
SVMは、ハードマージンSVMとソフトマージンSVMというものに大別されますが、今回はハードマージンSVMで考えます。この2つの違いについては、「第二弾:カーネルトリック編」に載せます。
キーワード
SVMで識別境界を求めるにあたり、重要なキーワードは以下の通りです。
・線形識別器
・マージン最大化
・点と直線の距離公式
・条件をつけて、一意に決める!
・最適化問題、ラグランジュの未定乗数法、双対問題
・KKT条件
線形識別器とは
SVMは線形識別器であるというように述べました。
線形識別器とは、以下のような線形の式(1次式、内積)で表せるような識別器のことです。
$f({\bf x}) = sgn({\bf w}^{T}{\bf x}+b) = sgn(w_0 \times x_0+ w_1 \times x_1+ ... + w_n \times x_n+b)$
ここで、$\bf x$は入力特徴量(その特徴空間における、ある点の座標を表すベクトル、つまり上の画像例なら、ある点(😊 や😱 )の座標$(x_0,x_1)$)です。特徴量の各要素($x_0$,...,$x_n$)にそれぞれ重み($w_0$,...,$w_n$)を掛けたものを足し合わせ、バイアス項bを足した式が、内積の形${\bf w}^{T}{\bf x}+b$となります。(「重み」や「バイアス項」が何かはここでは詳しくは触れません)
sgn関数は、入力( ${\bf w}^{T}{\bf x}+b$ )の値が正であれば1、0であれば0、負であれば-1を返します。
つまり、ある入力特徴量$\bf x$を入れた時、出力が1であればクラス1(😊 )に分類され、0であれば識別境界上にあると見なされ、-1であればクラス2(😱 )に分類されます。
すなわち、識別境界である超平面を表す式は、${\bf w}^{T}{\bf x}+b=0$となることがわかります。このような1次式(内積の形)で表される識別境界を使って入力特徴量を正しいクラスに分類できることを、線形分離可能といいます。
ここまでまとめたのが、下の図になります。最初に述べたように、学習データに対して、識別境界は引こうと思えば無数に引くことができますが、引き方は$\bf w$や$b$によって決定されます。なので、これらをうまく設定すれば、サポートベクタから最も遠くなるような識別境界を引くことができます。
つまり、SVMの最終目標は、「サポートベクタから識別境界への距離(マージン)を最大化するような、$\bf w$や$b$を決定すること」です。
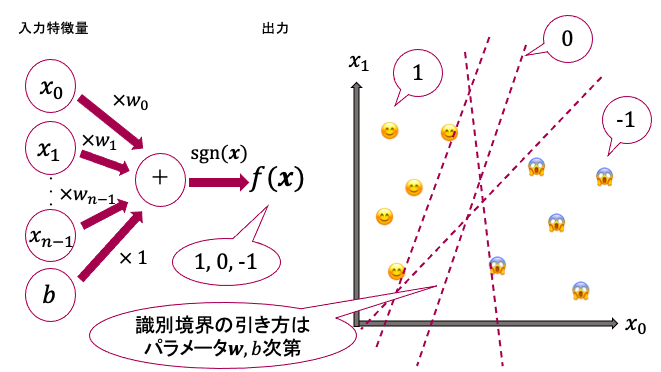
SVM(ハードマージンSVM)で識別境界を求める手順
では、ここからハードマージンSVMの学習における、$\bf w$や$b$の求め方を説明します。
まず、学習データのうちのi番目のデータ${\bf x}_i$について、識別境界との距離は、
$d_i = \frac{y_i({\bf w}^{T}{\bf x}_i+b)}{||{\bf w}||}$
と求めます。ここで、$y_i$はその点が本来分類されるべき正解クラスのラベルで「1か-1」をとります(正解クラスがクラス1(😊 )なら1、クラス2(😱 )なら-1、的な)。
ここで重要なのは、この式は、「正解クラスに分類される場合は正の値をとること」、「「点と線の距離公式」を点と超平面に適用した形であること」です。
前者については、 SVMでは前述のように${\bf w}^{T}{\bf x}_i+b$の値が正であるならクラス1(😊 )に、負であるならクラス2(😱 )に分類されるため、正しいクラスに分類できた場合には、分子の$y_i({\bf w}^{T}{\bf x}_i+b)$は正の値をとり、間違ったクラスに分類してしまった場合には負の値をとります。
後者については、以下の通りです。

さて、SVMは「サポートベクタ(最も識別境界に近い点)から識別境界までの距離を最大化する」ことは、「最も短い距離が、最大になるようにする」ということであるため、次のような処理手順となります。
1:最も距離が短い点i(つまり最小の$d_i$)を選択
2:選択した$d_i$が最も大きくなるように、最適な${\bf w}, b$を決定
式にすると以下の通りです。
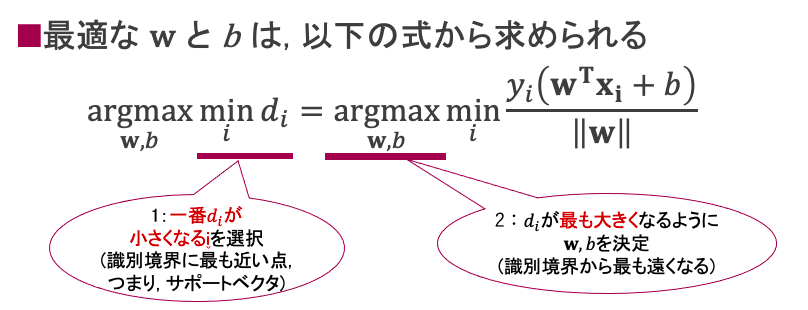
さあ、ここまでで、やりたいことに対する式を立てるところまでは来ました。
しかし、このままではいくつか問題点があります。
問題点
1:ある学習データを間違ったクラスに分類してしまうと$y_i({\bf w}^{T}{\bf x}_i+b)$は負の値になる。
2:識別境界の形が一つに決まったとしても、それを表す${\bf w}, b$が無限通り存在し、一意に定まらない。
3:そもそも識別境界をこれから求めようとしているのに、サポートベクタがどの点かなんてわかるはずない。
1については、$y_i({\bf w}^{T}{\bf x}_i+b)>0$と制約をつけて、問題を制限する必要がありそうです。
2について、識別境界の式は${\bf w}^{T}{\bf x}_i+b=0$ですが、例えばそれが直線であるとすると、以下のようにそれを表すパラメータの組み合わせは無限通り存在します。ただし、サポートベクタの入力特徴量を代入した時の値は変わってくるため、この値を制限すれば、パラメータを一意に定めることができそうです。

3について、これが最も重大な問題で、そもそもサポートベクタも識別境界もわかってなければ$d_i$を求めることすらできません。このような問題を解く時の方法として「ラグランジュの未定乗数法」が存在します。
考え方のポイント
・間違ったクラスに分類して$y_i({\bf w}^{T}{\bf x}_i+b)$が負の値になったり、識別境界を表す${\bf w}, b$が無限通り存在したりする状況を回避するため、問題に制約をあらかじめつける。
・サポートベクタや識別境界が何かは、この時点ではわからないため、ラグランジュの未定乗数法という解法を用いる
では、実際にやっていきましょう。
まず、問題に対して、以下のような制約条件をつけます。
$y_i({\bf w}^{T}{\bf x}_i+b)>=1$
この式は、問題点1と2を解決するために以下の条件をつけていることとなります。
・すべての学習データは間違ったクラスに分類されない。(問題点1)
・サポートベクタと識別境界との間の距離は1となる。(問題点2)
この制約をつけることで、問題の式は以下のように変形できます。
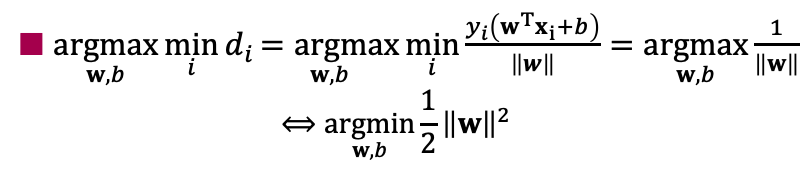
ここで、この後の計算を楽にするために、1/2を掛けているみたいです。
一旦ここまでを整理すると、以下のようになります。
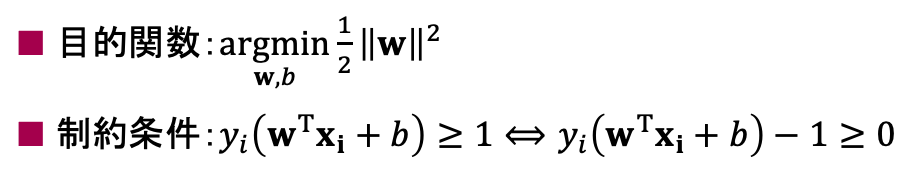
このように、制約条件の式を満たしながら、目的関数を最小化(最大化)する問題のことを「最適化問題」と呼びます。今回は目的関数が最小となるように、制約条件を満たす範囲で${\bf w}, b$を最適化します。
しかし、サポートベクタや識別境界が何かわからないという問題点3は未解決であり、この最適化問題から識別境界とサポートベクタを同時に求めていくことは困難です。そこで、ラグランジュの未定乗数法を用います。ラグランジュの未定乗数法は、今回のような制限付き最適化問題の代表的な解法であり、「ラグランジュ乗数αを導入し、目的関数と制約条件の式を一つの式にまとめ、「双対問題」を生成する」ということをやっています。
なんだか難しそうですね笑。
まずは、双対問題とは何者か、それを生成すると何が嬉しいのかについて紹介します。
双対問題とは
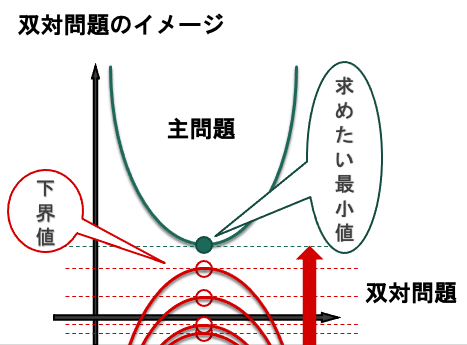
最適化問題において、今回のように目的関数の最小値を実際に求めるのが困難な場合があります。このような場合には、違う視点で攻めることが有効だったりします。すなわち、「求めたい最小値は、最低でもこの値よりは大きいだろう」という「下界値」を設定し、より良い(大きい)下界値を求めるという方法です。この時、「下界値を最大化したものが元の問題の解と一致する」というのは「弱双対定理」という定理で証明されています。このような考え方で、より良い下界値を求めようというのが双対問題です。
今回の問題では、「$\frac{||{\bf w}||^2}{2}$の最小値を求めるのは難しいけど、その下界値なら考えられるんじゃないか」という感じです。
(ちなみに、元の最適化問題のことを主問題と呼びます。また、主問題が目的関数を最大化する問題の場合、なるべく小さい上界値を求めるのがその双対問題となります。)
では、ラグランジュの未定乗数法を用いて、双対問題を作成していきましょう!
主問題は以下の通りです。
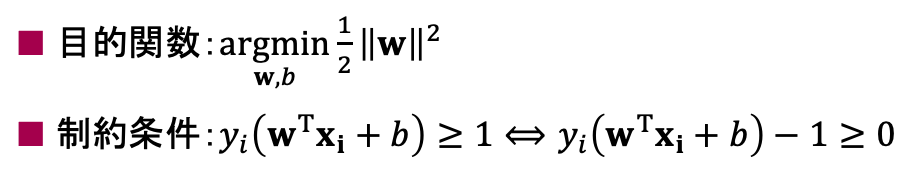
これにラグランジュの未定乗数法を用いて、一つの式にまとめたのが以下の通りです。

この式は、主問題の目的関数の下界値になります。
...なぜか?? 理由は以下のとおりです。
1:もしも$y_i({\bf w}^{T}{\bf x}_i+b)-1 < 0$となる入力特徴iが存在してしまう場合、iに対応するラグランジュ乗数$a_i$を超大きくすると、$L({\bf w}, b, {\bf a})$は超大きくなります。
2:しかし、今回は、$y_i({\bf w}^{T}{\bf x}_i+b)-1 >= 0$という制約条件をつけているため、すべての特徴iについて、$y_i({\bf w}^{T}{\bf x}_i+b)-1 >= 0$が成り立ちます。
3:これと、$a_i>=0$から、$\sum_{i=1}^{N}a_i \bigl\{ y_i({\bf w}^{T}{\bf x}_i+b)-1 \bigr\} >=0$となります。つまり、$-\sum_{i=1}^{N}a_i \bigl\{ y_i({\bf w}^{T}{\bf x}_i+b)-1 \bigr\} <=0$となりますね。
4:以上より、$\frac{||{\bf w}||^2}{2} >= \frac{||{\bf w}||^2}{2} -\sum_{i=1}^{N}a_i \bigl\{ y_i({\bf w}^{T}{\bf x}_i+b)-1 \bigr\} $となります。
すなわち、$\mathop{\rm argmin}\limits_{{\bf w}, b} \frac{||{\bf w}||^2}{2} >= \mathop{\rm argmin}\limits_{{\bf w}, b} L({\bf w}, b, {\bf a})$となるため、主問題の下界値になることがわかります。
さて、ラグランジュの未定乗数法を用いてこのように変形してきましたが、実はここで、また別の問題が生じています。それは、「今回の制約条件の式が不等式である」という点です。ラグランジュの未定乗数法の前提として、制約条件の式は「=0」の等式でなければならず、不等式の制約条件のままではラグランジュの未定乗数法を使って下界値を出すという操作をすることがそもそもできません。そこで、事前にKKT条件という条件をつけてあげることで解決します。
KKT条件 (厳密には以下の式だけでKKT条件というわけではない)
以下のような条件をラグランジュの未定乗数法を用いるために付与します。
$ a_i \bigl\{ y_i({\bf w}^{T}{\bf x}_i+b)-1 \bigr\} =0, i \in [n] $
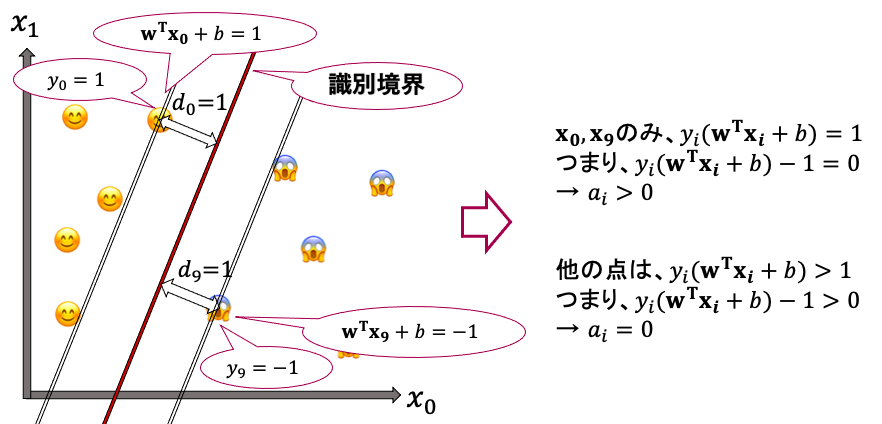
この式は、$a_i$か$y_i({\bf w}^{T}{\bf x}_i+b)-1$のどちらかが0という条件です。これをつけることで何が起こるのかというと、下の図のように、「$y_i({\bf w}^{T}{\bf x}_i+b)=1$となる点、つまりサポートベクタでのみ$y_i({\bf w}^{T}{\bf x}_i+b)-1 = 0$となるため$a_i>0$となり、それ以外のすべての点では$a_i = 0$となる。」ということが起こります。
逆に言えば、「$a_i > 0$なら$x_i$はサポートベクタ」とも言え、この考えはこの後重要な役割を果たします。
このKKT条件をつけたことで、ラグランジュの未定乗数法を用いる際の制約条件の部分が「=0」の等式となり、未定乗数法を用いて下界値をゲットすることができるようになりました。
また、サポートベクタ以外は$a_i = 0$となる、ということは、「サポートベクタについてしか考慮しない」というSVMの性質を表していると言えます。
余談ですが、今回は上記の条件式をKKT条件と書きましたが、実際にはこの式は複数存在するKKT条件のうちの一つです。他には、最初に付与した制約条件$y_i({\bf w}^{T}{\bf x}_i+b)>=1$もKKT条件と言ったりするみたいです。興味があればぜひ調べてみて下さい。
ここまでの整理
さて、ここまでを一旦整理しましょう。
・SVMの目的
マージン最大化した識別関数$f(x) = sgn({\bf w}^{T}{\bf x}_i+b)$の作成。
→ サポートベクタと識別境界の距離$d_i = \frac{y_i({\bf w}^{T}{\bf x}_i+b)}{||{\bf w}||}$の最大化。つまり、最適な${\bf w}, b$の取得。
・手順
1:制約条件「$y_i({\bf w}^{T}{\bf x}_i+b)>=1$」を付与。サポートベクタで左辺が1となる制約。これにより、最終的な識別境界が決まった際の$({\bf w}, b)$が一意に決まる。また、サポートベクタにおいて$d_i$の分子が1となる。
2:上記1の条件によって、$d_i$の最大化は、分母分子反転し$\mathop{\rm argmin}\limits_{{\bf w}, b} \frac{||{\bf w}||^2}{2}$という目的関数に置き換えれる。
3:上記1,2の制約条件と目的関数からサポートベクタと識別境界を同時に求めていくのは困難。そのため、このような問題の代表的な解法であるラグランジュの未定乗数法を用いて、下界値を作成する。ただし、そのためには制約条件の式が「=0」である必要があるため、KKT条件を付与してから、ラグランジュの未定乗数法を用いる。 (← 今ここ)
4:「下界値を最大化する(より良い下界値を見つける)」という双対問題を解くことで、主問題が解ける(弱双対定理)。これにより、最適な${\bf w}, b$をゲット。
ここまでで、3までは終わりました。では、最後、4を行っていきましょう。
双対問題の作成と解法
改めて、ここまでで主問題の目的関数の下界値$\mathop{\rm argmin}\limits_{{\bf w}, b} L({\bf w}, b, {\bf a})$を取得しました。これは${\bf w},b$について最小化しているので、$\mathop{\rm argmin}\limits_{{\bf w}, b} L({\bf w}, b, {\bf a})$は最小値なので、${\bf w}, b$について微分した値が0となります。すなわち、
$\frac{ΔL} {Δ\bf w} = {\bf w} -\sum_{i=1}^{N}a_i y_i{\bf x}_i = 0$
$\frac{ΔL} {Δb} = \sum_{i=1}^{N}a_i y_i= 0$
となります。
これらの式より、$\mathop{\rm argmin}\limits_{{\bf w}, b} L({\bf w}, b, {\bf a})$を以下のように変形することができます。
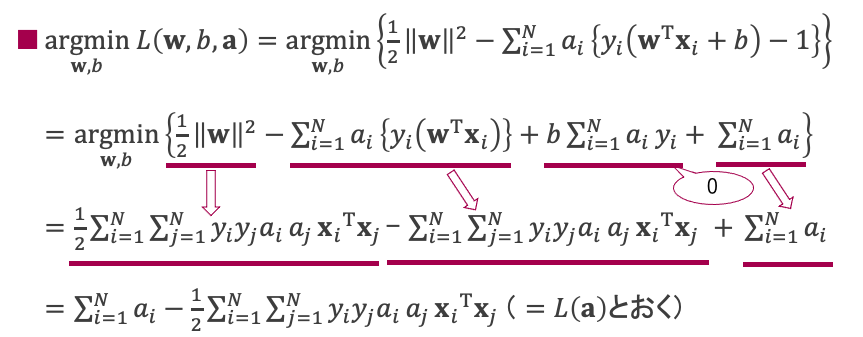
この変形により、下界値$\mathop{\rm argmin}\limits_{{\bf w}, b} L({\bf w}, b, {\bf a})$をラグランジュ乗数${\bf a}$だけを用いて、$L({\bf a})$ と表すことができるようになりました。
前述したように、双対問題はより良い下界値を求めることを目的とします。つまり、$L({\bf a})$を${\bf a}$について最大化すれば良いこととなります。
これにより、最終的に以下のような双対問題となります。
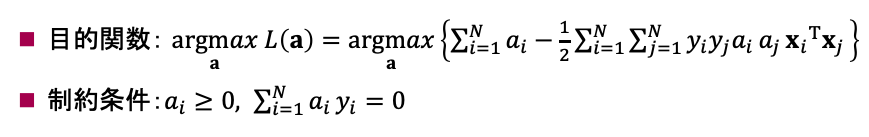
制約条件は、これまで出てきた条件と微分の式をまとめたものなので、何のことだっけ?という方はラグランジュの未定乗数法あたりから見返してみてください。
ここまでで、双対問題を立てるところまでできました!
最後、ここから以下の手順によって、マージンを最大化した識別境界及び識別関数(つまり最適な ${\bf w}, b$)が求まります!
1:双対問題をSMOアルゴリズムなどを用いて、解くことで最適な ${\bf a}=(a_1, ..., a_N)$ が決まる。
2:サポートベクタを決定(上記1で、$a_i>0$となる点$x_i$)。
3:${\bf w}, b$も求まる(上記1,2で得られた$a_i, x_i$を微分の式に代入するだけ)。
4:識別境界${\bf w}^{T}{\bf x}+b = 0$、識別関数$f({\bf x}) = sgn({\bf w}^{T}{\bf x}+b)$が決定。
以上となります!
SMOアルゴリズムは、今回のような最適化問題を解くためのアルゴリズムの一つみたいです。
詳細は省略しますが、興味ある方は調べてみてください。
まとめ
今回はSVM(ハードマージンSVM)が識別関数(識別境界)をどうやって求めているのかについてご紹介しました。
改めて、私がポイントだと思う部分は以下の通りとなります。
・やりたいことはマージン最大化。でも、サポートベクタと識別境界を同時に考えるのは難しい。
・制約条件をつけたり、ラグランジュの未定乗数法で双対問題を作成することで、解ける形にする。
長くなりましたが、お疲れさまでした!
次回は、ハードマージンSVMとソフトマージンSVMの違いや、カーネルトリックについて書こうと思います。