今年から12月25日はクリスマスじゃなくて超関数の日にしましょう

はじめに

この記事は明治大学 Advent Calendar 2018の最終日25日です。今日はクリスマスです。メリークリスマス。恋人と過ごすのも素晴らしいと思いますが、今年から12月25日は超関数の日になるので、超関数と過ごしましょう。

目標

超関数の定義をじっくり観察して、超関数を理解する。

(注意): 本記事で「超関数」は「シュワルツ超関数」の意味で使います。

超関数とは？

超関数とは「滑らかで台がコンパクトな関数全体上の連続な線形汎関数」です。細かな言葉の説明は後にしますが、要するに我々が普段使う意味での関数の一般化だと思ってもらえれば良いです。

超関数が必要な理由(デルタ関数を通して)

確率論ならとか物理学なんかを学んでいるとデルタ関数という一点だけ値が無限な関数を考えることが出てきます。その大体の場合はこんな感じで「定義」されるはずです。

\delta(x) = \begin{cases}
\infty, \ \quad (x = 0) \\
0, \ \quad (x \ne 0)
\end{cases}, \quad \int_{-\infty}^\infty \delta(x) dx = 1.

確率論では分散0平均0な正規分布に対する確率密度関数と捉えることができたり、物理では原点にある点電荷と捉えたりできたりして、妥当な定義のように見えますが、ちょっと待ってください。デルタ関数を上のように「定義」した場合、本当に積分は1になるのでしょうか？ルベーグ積分論では「ほとんど至るところ0な関数を積分したら1にならずに0なる」のです。なので、上の「定義」は数学的に良くないのです。

超関数はこのデルタ関数を厳密に定義することを可能にします。式だけチラ見せしますが、デルタ関数を超関数としてみるとき、以下のように「普通の関数」$f(x)$の$x = 0$での値を取り出せるものとするのです。¹$$\int_{-\infty}^{\infty} f(x) \delta (x) dx := f(0).$$

超関数の定義

それでは超関数の定義をしましょう。

超関数とは滑らかで台がコンパクトな関数全体上の連続な線形汎関数のことである。

色々見慣れぬ言葉があるかもしれないので、説明していきます。

本節では、「イメージ図や日本語による説明$\to$数式を用いた数学的な表現」という構成で書いていきます。厳密に数学でどう表現されるか知りたい方のみ数式部分を追っていただければ良いと思います。

また、数学的なバックグラウンド(特に位相空間論)は脚注に書いてありますので、よくわからなかったらそちらを見てください。

滑らかで台がコンパクトな関数全体

滑らかで台がコンパクトな関数とは例えば下図のような関数のことをいいます。

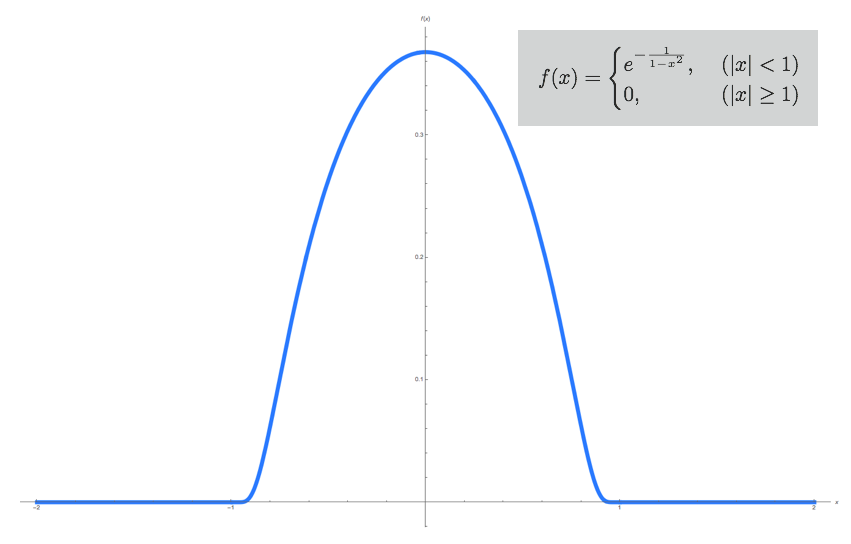
まず、定義域が$\mathbb{R}^n$全体で連続な関数$f(x_1, \ldots, x_n)$を考えましょう。その$f$が滑らかであるというのは、どの変数でも何回でも微分できて、その微分した結果がまた$\mathbb{R}^n$全体で連続になるような関数のことを言います。

また、関数$f(x_1, \ldots, x_n)$の台がコンパクトであるとは、何なのかを説明するために、まずは関数の台という言葉を説明しましょう。関数$f$の台とはその関数が$0$でないような$(x_1, \ldots, x_n)$全体のことを言います。英語ではsupport(サポート)といいますが、イメージとしては関数をサポートしているような部分です。

その台がコンパクトとはどういうことでしょう。$\mathbb{R}^n$の中の集合がコンパクトであるとは、その集合が有界な閉集合であることと同じです²。 要するに、大きさが有限で境界も含んでいるような集合だということです。

以上をまとめると、滑らかで台がコンパクトな関数とは、何回でもどの変数でも微分した結果が連続になって、その関数の値が$0$以外の値を取る場所が無限に広がっていないような関数のことを言います。そのような関数全体のことを「滑らかで台がコンパクトな関数全体」として$\mathcal{D}$と表します。

数学的には次のように表現します。$\mathrm{supp} \{f\}$を$f$の台、$\alpha = (\alpha_1, \ldots, \alpha_n) \in (\mathrm{Z}_{\ge 0})^n$を多重指数としたとき、$\partial^{\alpha}f$を$f$の$\alpha$階微分とすれば³、

\mathcal{D} := \{f: \mathbb{R}^n \to \mathbb{R} \mid \mathrm{supp} \{f\}: \mathrm{compact}, \ \partial^{\alpha}f: \mathrm{continuous} \ (\forall \alpha) \}

と表せます。

「滑らかで台がコンパクトな関数全体」の位相

まず、滑らかで台がコンパクトな関数全体$\mathcal{D}$はベクトル空間になるということを抑えときましょう。これはどういうことかというと、滑らかで台がコンパクトな関数同士を足し合わせたり、何か実数を掛けたりしても、再び滑らかで台がコンパクトな関数になるということです。

また、次の小節で「連続」という概念を考えていく上で、$\mathcal{D}$に「位相を入れる」必要があります。「位相を入れる」とはどういうことかというと、「滑らかで台がコンパクトな関数の列」に対して、その極限を定義することを意味します⁴。(位相を考える重要性はこの脚注に書いてあります。)

では、どのようにして位相を入れればよいかというと、滑らかで台がコンパクトな関数の列$\{f_n\}$が$f$に収束することを、「全ての$f_n$の台を含むような十分大きなコンパクトな集合が存在して、$f_n$の全ての導関数がそれぞれある連続な関数に収束する」こととします。^5

つまりは、位相をどう定義するかというと、

\begin{align}
f_n \to 0 & \ \mathrm{in} \  \mathcal{D} \\
\overset{\mathrm{def}}{\iff} & (\exists K \subset \mathbb{R}^n: \mathrm{compact} \ \mathrm{s.t.} \ \mathrm{supp}\{f_n\} \subset K \  (\forall n)) \ \\
& \land \ (\partial^{\alpha} f \to f_\alpha \in \mathcal{D})
\end{align}

とするわけです。ここで、$0$への収束のみに関して書いてある理由は、前述の通り$\mathcal{D}$がベクトル空間であることに起因しています。

連続な線形汎関数

まずは、「超関数論」に絞って線形汎関数というものを定義していきましょう。一般に汎関数とは「関数」を複素数に写す写像のことを言います。よって、$\mathcal{D}$から複素数全体$\mathbb{C}$への写像$T: \mathcal{D} \to \mathbb{C}$が線形汎関数とはこの写像が線形な写像であれば良いということです。つまり、$f$と$g$が両方とも滑らかで台がコンパクトな関数だとして、$\lambda_1$と$\lambda_2$を複素数としたときに、

T(\lambda_1 f + \lambda_2 g) = \lambda_1T(f) + \lambda_2 T(g)

となることを言います。

この線形汎関数が連続であるということは、普通の関数の連続と同じようにして、$f_n$が$f$が上の小節で定義したような$\mathcal{D}$における収束の仕方で収束したときに、$T(f_n)$が$T(f)$に収束することとしましょう。すなわち、

f_n \to f \ \mathrm{in} \ \mathcal{D} \Longrightarrow T(f_n) \to T(f) \  \mathrm{in} \ \mathbb{C}

が成り立つこと$T$が連続ということにしましょう。このような$T$を$\mathcal{D}$上の連続な線形汎関数と呼びます。

また、このような線形汎関数に対する$\mathcal{D}$のことをテスト関数の空間と呼び、$\mathcal{D}$の要素である関数$f$のことをテスト関数と呼びます。ちょうど線形汎関数の性質をテストするための関数という具合です。次々小節にて、これに関する筆者がしている直感的な理解を説明します。

超関数

以上の小節の話を全てまとめましょう。まず、滑らかで台がコンパクトな関数全体$\mathcal{D}$を定義しました。次に$\mathcal{D}$に位相を入れました。そして、$\mathcal{D}$上の連続な線形汎関数を定義しました。

これで超関数の定義の役者が全て揃ったわけです。もう一度定義を振り返ってみましょう。

超関数とは滑らかで台がコンパクトな関数全体上の連続な線形汎関数のことである。

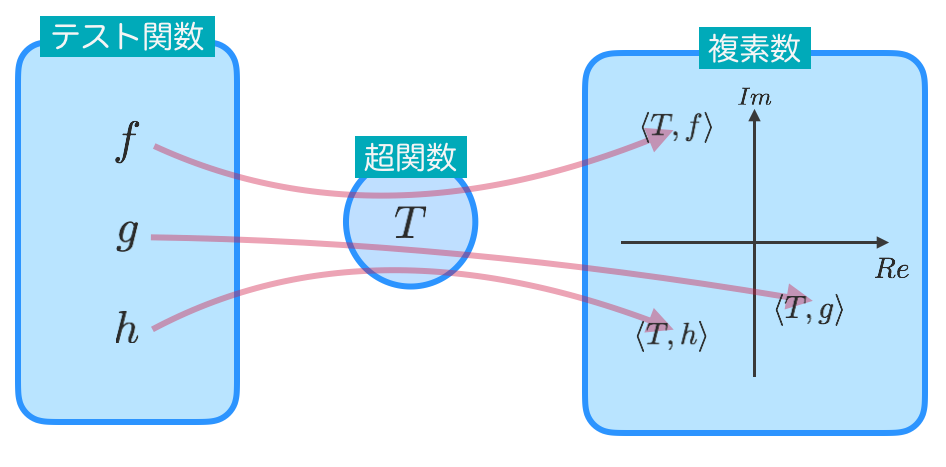
つまり超関数とは$\mathcal{D}$上の連続な線形汎関数$T: \mathcal{D} \to \mathbb{C}$のことをいいます。また、上では$f$における超関数$T$の値を$T(f)$と書きましたが、これからは$\langle T, f \rangle$と書くことにします。左に超関数を置いて、右に滑らかで台がコンパクトな関数を起きます。

超関数の直感的理解(おまけ)

この節はおまけです。本記事の筆者がどうやって超関数を理解しているかを説明します。「連続な線形汎関数」節で$\mathcal{D}$のことをテスト関数の空間と呼びました。これは得体の知れない超関数という対象を理解するために、比較的馴染み深い「滑らかで台がコンパクトな関数」によってその超関数をテストすることで、よくわかっている複素数の空間で理解しようという試みなのです。

物理現象で例えてみましょう。超関数とはなにかの現象です。その現象を我々は滑らかで台がコンパクトな関数というテスト関数を用いて観測することで、複素数という観測量を得ることができます。イメージとしては下のような感じです。

超関数の例

局所可積分関数

局所可積分関数とはいわゆる普通の関数で、あまり突飛なことが起きないような関数です。ちゃんとした定義をすると、局所可積分とは任意のコンパクトな集合上で(ルベーグの意味で)可積分な関数のことを言います。

さて、$f$を$\mathbb{R}^n$上の局所可積分関数としたとき、これを超関数として見る方法があります。$\varphi$を$\mathbb{R}^n$上の滑らかで台がコンパクトな関数として、以下のように超関数$T_f$を定義しましょう。 $$\langle T_f, \varphi \rangle := \int_{\mathbb{R}^n}f(x)\varphi(x)dx.$$

こうすることで、局所可積分関数は超関数として見なすことができます。つまり、超関数とはこの意味で、「普通の関数」の一般化として見なすことができるのです。

デルタ関数

さて冒頭にて紹介したデルタ関数を超関数として厳密に定義しましょう。デルタ関数とは以下のように定義する超関数です。$$\langle \delta, \varphi \rangle := \varphi(0)$$

ここでは一切積分が出てきていません。そうです、超関数とはあくまでもテスト関数一つ一つに対して複素数をあてがうものなので、積分による定義をする必要はないのです。ただ、形式的に⁵積分の記号を用いて下のように表すことがあります。
$$\langle \delta, \varphi \rangle = \int_{-\infty}^\infty \delta(x)\varphi(x)dx = \varphi(0)$$

こうすることで、従来の積分と同様の扱いをすることができるようになることがあって便利なのです。

超関数の微分

超関数はなんと微分できます。例えば、1階微分可能で１階導関数も連続であるような関数$f: \mathbb{R} \to \mathbb{R}$を考えましょう。これは局所化積分関数であるので、上の例で見たように超関数$T_f$として見なすこともできます。この超関数を$x$に関して微分してみましょう。

\begin{align}
\langle \frac{dT_f}{dx}, \varphi \rangle & = \int_{-\infty}^{\infty} \frac{df}{dx}(x) \varphi(x)dx \\
& = \left[f(x)\varphi(x)\right]_{-\infty}^\infty - \int_{-\infty}^\infty f(x)\frac{d\varphi}{dx}(x)dx \\
& = - \langle T_f, \frac{d\varphi}{dx}\rangle
\end{align}

なお、1行目から2行目は部分積分をして、2行目から3行目は1項目は$\varphi$の台がコンパクトなので、十分遠方では値が0になることから消えてしまい、2項目は超関数として見なせます。

上の考察では$f$が微分可能であるからできた考察でした。しかし、数学はときに大胆です。上の式変形は一切忘れてしまい、計算結果だけを見て超関数の微分を下のように定義してしまおうというのです。つまり、超関数の微分の定義を$$\langle \frac{dH}{dx}, \varphi \rangle := -\langle H, \frac{d\varphi}{dx}\rangle$$としてしまおうというのです。マイナスを出して、微分をテスト関数側に押し付けるのです。こうすることでデルタ関数の微分なんかもできたりします。$$\langle \frac{d\delta}{dx}, \varphi \rangle = -\langle \delta, \frac{d\varphi}{dx} \rangle = -\frac{d\varphi}{dx}(0)$$といった具合です。

また、テスト関数の定義された空間の次元によっては超関数の偏微分もできますし、微分を何回も繰り返せば、超関数の高階微分もできます。これは次のようにすればよいのです。$$\langle \partial^\alpha T, \varphi \rangle = (-1)^{|\alpha|}\langle T, \partial^\alpha \varphi \rangle $$

発展的な話

この節は少し発展的です。細かな説明はしません。

超関数全体に対する位相

超関数全体にも位相が入ります。すなわち、超関数の列の極限を考えることができます。まず、一つ留意しておく点として、超関数全体はベクトル空間です。線形性の確認は読者に任せます。

超関数列$\{T_n\}$を考えましょう。この列が超関数$T$に収束するとは、任意のテスト関数$\varphi$に対して、$$\langle T_n, \varphi \rangle \to \langle T, \varphi \rangle \ \mathrm{in} \ \mathbb{C}$$が成り立つことを言います。一般に位相の入れ方は沢山ありますが、このような位相のことを弱-*位相(じゃくすたーいそう)と呼びます。⁶

一見、発展的には見えないかもしれませんが、このような位相を考えたときに、超関数列の収束先がしっかりと再び超関数になることは決して当たり前なことではありません。このことを保証してくれるのがBanach-Steinhausの定理というものなのですが、この説明はまた別の場所に譲ります。

別の「超関数」

本記事では超関数を滑らかで台がコンパクトな集合全体$\mathcal{D}$上の連続な線形汎関数と定義しました。ですが、実はこのテスト関数の空間を色々と取り替えることで別の「超関数」を考えることができます。例えば、急減少関数という関数全体をテスト関数の空間として取れば、緩増加超関数として捉えることができます。他にも$L^p$空間をテスト関数として捉えれば$\frac{1}{p} + \frac{1}{p'} = 1$を見たす$L^{p'}$空間の要素が「超関数」となったりします。⁷

まとめ

超関数の定義を見て、例を見て、微分ができることを学びました。

参考文献

溝端「偏微分方程式論」
シュワルツ「超関数論」

1. ここで使う積分記号はあくまでもただの記号であって、リーマン積分やルベーグ積分で使われる積分記号ではありません。形式的にこうやって書こう、とだけのものです。 ↩

2. 位相空間論において、ある位相の定まった空間$\Omega$の部分集合$K$がコンパクトであるとは「任意の開被覆に有限な部分被覆が存在する」ことを言います。ですが、$\Omega = \mathbb{R}^n$としたとき、Haine-Borelの定理が「$K$がコンパクトであることと、その$K$が有界閉集合であることは同値」だということを保証してくれます。 ↩

3. $\partial^\alpha f := \frac{\partial^{\alpha_1 + \cdots + \alpha_n}}{\partial x_1^{\alpha_1} \cdots \partial x_n^{\alpha_n}}f$ということです。文献によっては$D^{\alpha}f$と書いているものもあります。紙面の節約になりますね。 ↩

4. 「連続」という概念を考える上で位相を入れる必要を軽く説明します。例えば普通の関数$f: \mathbb{R} \to \mathbb{R}$が$x \in \mathbb{R}$において連続であるかどうかを確認したいなら、$x_n \to x$となる数列$\{x_n\}$を考えて$f(x_n) \to f(x)$であることを確認すればよいです。このようにして、定義域である$\mathbb{R}$と値域である$\mathbb{R}$に関して極限を考える必要、すなわち「位相が入っている」必要があるのです。当然、$\mathbb{R}$には我々が普通に扱っているような「位相が入っている」わけですが、これから考えたいのは「関数全体」の位相です。「何が何にどうやったら収束するのか」という条件を考えないといけないのです。 ↩

5. 数学では「形式的」という言葉がしばしば出てきます。これは数学的には厳密ではないけど、あくまでも形だけとりあえずやってみたり書いてみたりする、ということを意味します。 ↩

6. 他にも強位相や、弱位相などがありますが、超関数においてこれらは「同じ位相」になります。つまり、どの位相で定義しても同じ超関数列は同じ超関数に収束します。 ↩

7. $L^{p'}$空間を超関数の空間と呼ぶのは少し抵抗がある場合、双対空間や共役空間と呼ぶ方が自然かもしれません。 ↩