はじめに
ポケモンには様々なコレクション要素が存在しています。1 最も代表的なのはこのようにポケモン全種類を集めることです。
やったー!ポケモン全898種類を1匹ずつ手に入れたぞ!!小さい頃からの夢を達成した pic.twitter.com/2P2hbq2DUc
— りゅうふじわら(現象) (@ryunryunryun_) February 18, 2021
Pokémon HOMEには「わざ」図鑑があります。図鑑があるからには、埋めたくなるのが人の性です。よって、本記事では「わざ」をコレクションすることに着目します。
本記事の構成
本記事は以下のような構成になっています。
- ポケモンのわざをコレクション
- わざコレクション問題を説明して簡単な例を考えます
- 最大フロー問題によって解決しよう
- 最大フロー問題でわざコレクション問題を解きます
- こだわり話
- 筆者のこだわりに合うように問題を改良します
- 実際のプログラムと結果
- 解いたプログラムと結果を載せます
ポケモンのわざをコレクション
「わざ」を集めるとは具体的にどういうことを指すを以下のように定義します。
~わざコレクション問題~
全ての「わざ」を被りのないように、複数のポケモンに覚えさせる。ただし、ポケモンは被りなく選ぶものとする。
どうせコレクションするのなら、面白く集めたいわけです。ただ集めるだけなら、ドーブル2をたくさん捕まえて、全てのわざを覚えさせればいいのですが、個人的にはそれは面白くありません。(ドーブルファンの方、すみません。)そのため、多くの種類のポケモンを使って、わざを集めることを目標とします。
重要な制約: 覚えられるわざの数
本問題を考える上で、ポケモンならではの制約があることを述べておきます。特に一つ目の制約は、以下の節でとても重要になります。
- すべてのポケモンは最大4つまでしかわざを覚えられない
- 各ポケモンは覚えられるわざが限られている
簡単な例
いきなり全種類のわざやポケモンを考えるのは大変なので、簡単な場合を考えてみましょう。
この世界にはニドキング3とピカチュウのみがいるとします。また、わざも以下の表のように数種類しかないとして、覚えられるわざの対応表にしてみます。
(注意): 次の表の「わざ1 ~ 4」は覚えている「わざ」ではなく、レベルアップ・タマゴ技・教え技・わざマシン等で覚えられる「わざ」 です。
| ポケモン | わざ1 | わざ2 | わざ3 | わざ4 |
|---|---|---|---|---|
| ニドキング | じしん | にどげり | かみなり | つのでつく |
| ピカチュウ | しっぽをふる | 10まんボルト | かみなり | でんこうせっか |
この世界だと、ニドキングとピカチュウ両方がかみなりを覚えられます。被りがないように全てのわざを各ポケモンに覚えさせるには、例えばピカチュウにかみなりを覚えてもらって、
| ポケモン | わざ | わざ | わざ | わざ |
|---|---|---|---|---|
| ニドキング | じしん | にどげり | つのでつく | -- |
| ピカチュウ | しっぽをふる | 10まんボルト | かみなり | でんこうせっか |
のように覚えさせればよいです。こうすることで無事に 被りなく 七種類のわざが 被りなく 各ポケモンに覚えさせることができました。
最大フロー問題によって解決しよう
前節の例ではポケモン二匹、わざ七つと簡単な世界だったので目の子で簡単に組み合わせを求められました。しかし、実際の世界にはポケモン4と764種類のわざ5もあります。これをどう割り振るかなんて至難のわざです。
本問題を解決するために最大フロー問題に当てはめることを試みます。
最大フロー問題
最大フロー問題(Wikipedia)とは、有向ネットワーク上の最適化問題の一つです。早稲田大学 早水桃子さんのYouTubeチャンネルの「離散数学入門#8: 最大流問題(1):フローネットワークの基礎知識」にて非常にわかりやすく説明されているので詳しくはそちらを参照してください。「離散数学入門」シリーズの他動画もおすすめです。
ざっくりと説明します。あるスタート地点からゴール地点まで、いくつかの地点を経由しながら物を運ぶことを考えます。各道(有向辺)には、運べる物の許容量が定められているとし、この許容量を超えるような物を運ぶことはできないとします。最大フロー問題とは、ゴール地点まで運べる物の最大量とその運び方を求める問題です。
実問題を最大フロー問題で解決する際に必要なことは、
- 有向ネットワーク
- スタートとゴールのノード
- 各辺の許容量
をどう設定するかです。
わざコレクション問題を最大フロー問題で解釈
さて、わざコレクション問題に戻りましょう。再度、簡単な例を用いて考えてみます。この簡単な例を最大フロー問題を用いて捉え直します。以下のようなポケモンと覚えられる「わざ」の対応表を考えていました。
| ポケモン | わざ1 | わざ2 | わざ3 | わざ4 |
|---|---|---|---|---|
| ニドキング | じしん | にどげり | かみなり | つのでつく |
| ピカチュウ | しっぽをふる | 10まんボルト | かみなり | でんこうせっか |
上の表を次のような有向ネットワークとして解釈してみます。各わざから、そのわざを覚えられるポケモンへと有向辺を繋ぎました。各辺には、 ポケモンは同じわざを一つだけしか覚えられないという気持ちのもと、容量を$1$と設定します。
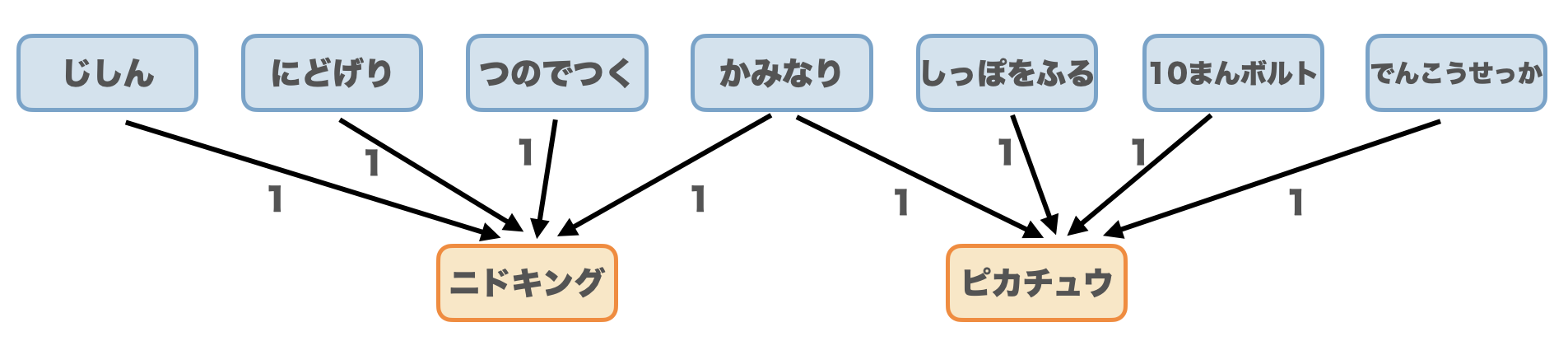
次に、わざコレクション問題の設定である、各わざをいずれかのポケモン一種類のみに覚えさせるということを考えます。つまり、かみなりから出ている二本の辺の内、どちらか一本を選ばないといけないわけです。
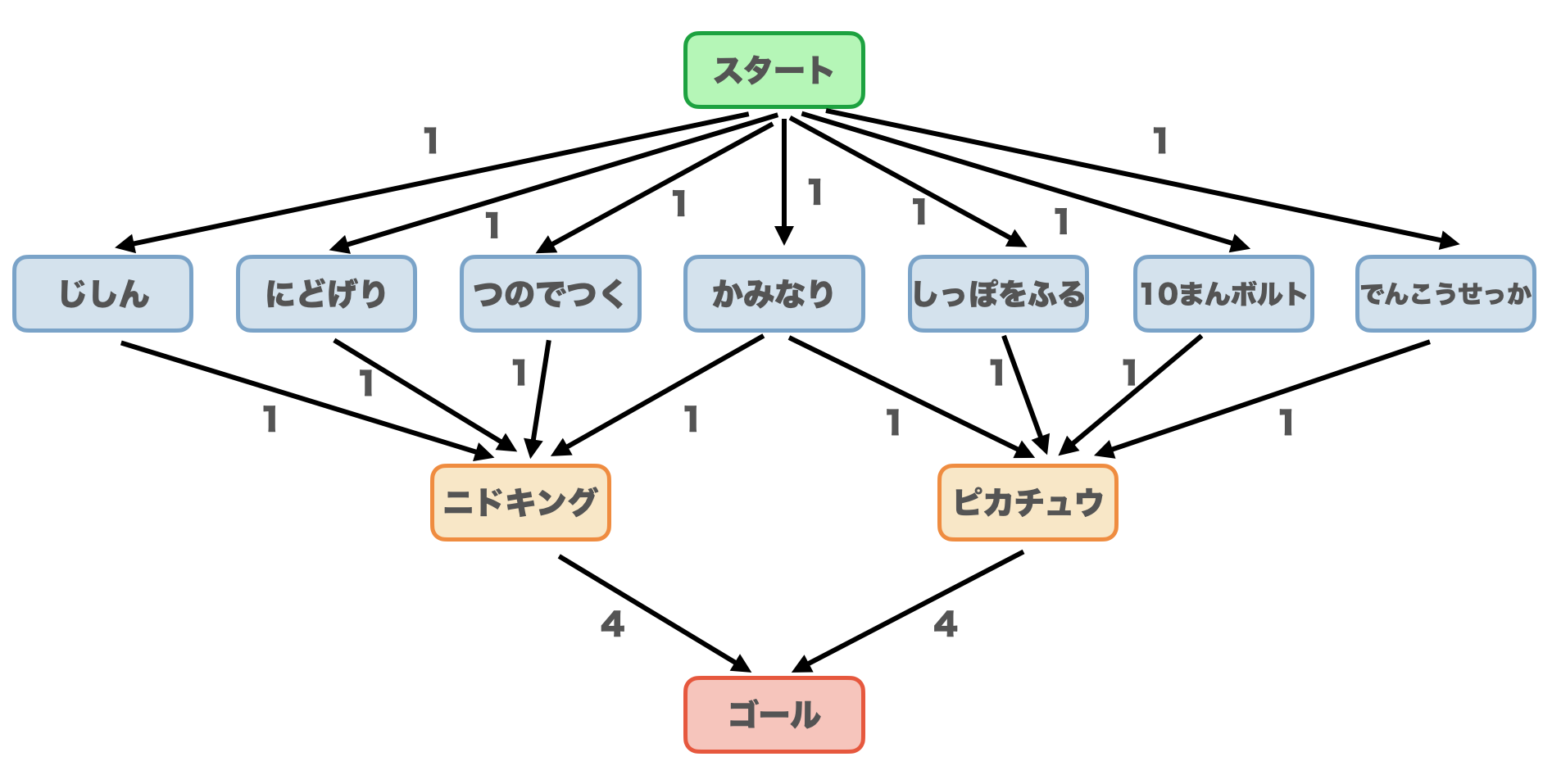
また、前節で述べた制約の すべてのポケモンは最大4つまでしかわざを覚えられないことを考えます。すなわち、ニドキングもピカチュウも四本入ってきている辺の内、最大で四本までしか辺を選べません。
これらをまとめた有向ネットワークが下のとおりです。各わざに向かっている辺とその容量$1$は一つのわざは一種類のポケモンにのみしか覚えさせないことを表現しています。各ポケモンから出ている辺とその容量$4$はすべてのポケモンは最大4つまでしかわざを覚えられないことを表しています。
この有向ネットワークと容量に対して、最大フローを求めてみると、例えば以下のような結果が得られます。ここで、$1/1$や$0/1$などは、許容量(右の量)に対して、フロー(左の量)がどれくらいかを表したものです。
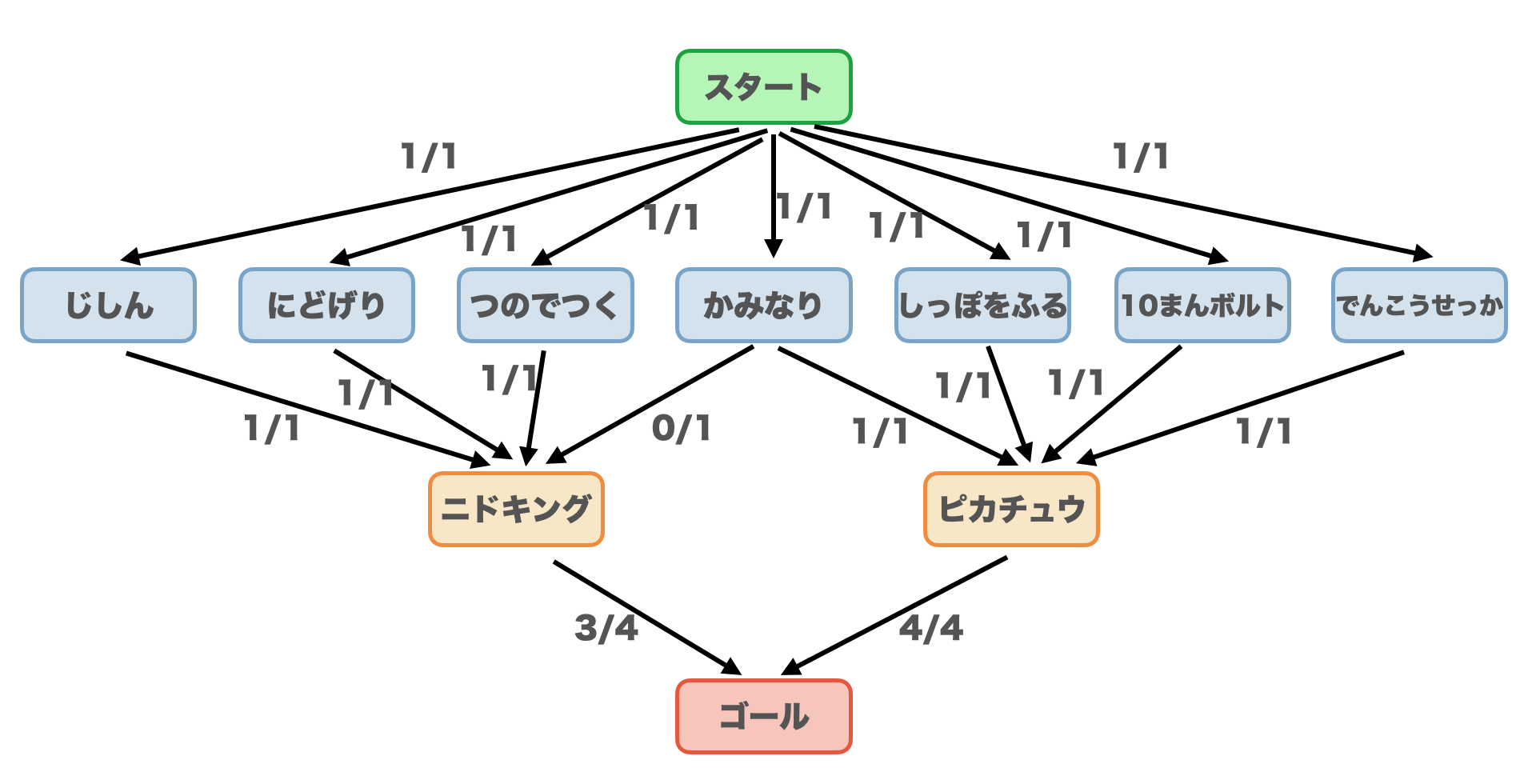
この最大フローに関する図を解釈します。スタートから出る有向辺の全てが$1/1$なので、全てのわざがいずれかのポケモンに覚えられていることがわかります。かみなりからニドキングに出ている辺が$0/1$なので、ニドキングにはかみなりを覚えさせないことを意味しています。一方で、かみなりからピカチュウは$1/1$なので、ピカチュウにはかみなりを覚えさせましょう。他のわざからポケモンへの辺はすべて$1/1$になっているので、それらのわざも対応したポケモンに覚えさせます。最後に、ニドキングからゴールへ$3/4$、ピカチュウからゴールへ$4/4$であることはそれぞれ、三種類・四種類のわざを覚えさせることに対応しています。
以上の解釈は以前の章で、目の子で求めた組み合わせと合致しています。
| ポケモン | わざ | わざ | わざ | わざ |
|---|---|---|---|---|
| ニドキング | じしん | にどげり | つのでつく | -- |
| ピカチュウ | しっぽをふる | 10まんボルト | かみなり | でんこうせっか |
わざコレクション問題の解き方
ポケモンと覚えられるわざの対応表から、最大フロー問題を用いることで、わざコレクション問題の答えを得られました。流れをまとめます。
- 各わざから、そのわざを覚えられるポケモンへと容量1の有向辺を繋ぐ
- スタートとゴールの頂点を用意する
- スタートから各わざへと容量1の有向辺を繋ぐ
- 各ポケモンからゴールへと容量4の有向辺を繋ぐ
- 1 ~ 4で作成した有向ネットワークで最大フロー問題を解く
- 最大フローにて、スタートから出る辺の全てのフローが1であればそれが答え
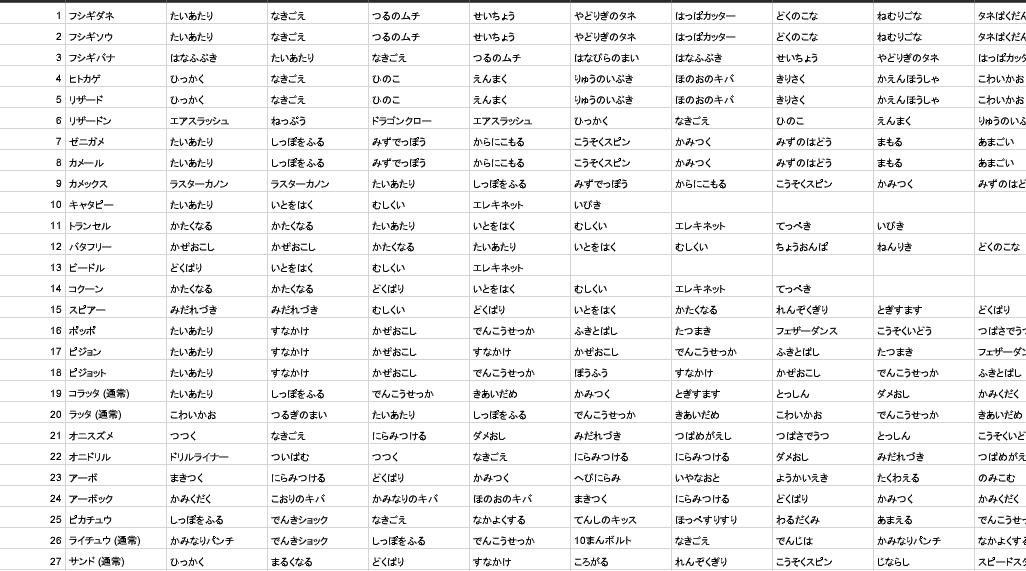
この流れで実際のポケモン905匹、わざ764種類におけるわざコレクション問題についても解を求めることができるのです。実際の表の一部を以下に載せます。この表をもとに有向ネットワークを構成して最大フロー問題を解けば、答えが得られます。
こだわり話
わざコレクション問題を最大フロー問題に置き換えて解く方法を考えてきました。しかし、それによって得られる結果は、必ずしもコレクション的観点から美しいわけではありません。本節では、このこだわりにより生ずる問題点と解決方法をつらつらと書いていきます。
わざ覚えさせないポケモン多すぎ問題
実際のデータに対して、本アルゴリズムを適用すると、実は1種類のわざのみしか覚えさせなかったり、1種類もわざを覚えさせる必要のないポケモンばかり出てきます。これはわざの総数に対して、ポケモンの総数が多すぎることに起因しています。ここまでポケモン905種類と言いましたが、フォルムチェンジやリージョンフォームを含むと1063種類6います。1063種類が仮に4つわざを覚えれば1063 × 4 = 4252種類のわざを覚えられますが、実際のわざは764個しかありません。ポケモンが余るのです。
コレクションする上では無駄はしたくありません。扱うポケモンの数は少なければそれに越したことはありません。そのため、わざコレクション問題を改良して、次の問題を考えることとします。
~改良わざコレクション問題~
全ての「わざ」を被りのないように、複数のポケモンに覚えさせるときの、最小のポケモン数はいくつか。また、その際のポケモンとわざの組み合わせも求めよ。ただし、ポケモンは被りなく選ぶものとする。
改良問題の前半部分である「最小のポケモン数」は、単純な計算で推定することができます。764種類のわざを4種類ごとに分割して、それぞれの分割を異なるポケモンに覚えさせればいいわけです。つまり、764 ÷ 4 = 191種類のポケモンが最小数の候補です。あくまでも候補で、実際に191種類のポケモンのみで答えが作れるかは要検証ですが、後に分かる通りになんと191種類が答えです。
適切なポケモンの選び方
改良わざコレクション問題の後半部分を考えます。ここでは、上で求めた通り191種類のポケモンを選べばよいだろうと仮定して進めます。ポケモンとわざの表から適切に191種類のポケモンを選び、764種類のわざを分配できるかを調べます。どの191種類を選べばいいかについて、いくつか条件を考察します。
例えば、「へんしん」しか覚えないメタモンを191種類に含んでしまうと、その時点で191種類に収めることはできなくなります。他にも、「きょじゅうざん」を唯一覚えるザシアンを191種類に含めないと、全てのわざを網羅できなくなります。
「へんしん」と「スケッチ」
全わざの内、「へんしん」と「スケッチ」はかなり特殊なわざです。「へんしん」は、メタモン・ドーブル・ミュウの三体のみが覚えられるわざです。「スケッチ」はドーブルのみが覚えます。そのため、2つの技に共通するドーブルは絶対に選ばれなくてはなりません。しかも、ドーブルは出演する作品7に存在するわざ全てを覚えられるので、余った二枠はドーブル以外の190種類のポケモンに覚えさせられない2種類のわざを覚えさせる必要があります。
結局どのポケモンを選べば良いのか
以上をまとめると、191種類のポケモン達は次のように特徴づけられるはずです。
- 各ポケモンは4種類以上のわざを覚える必要がある
- 唯一無二のわざを覚えるポケモンは必ず含まれる
- ドーブルを必ず含み、「へんしん」と「スケッチ」を必ず覚えさせる
この三点を守りながら適当に191種類を選んで、764種類のわざと一緒に最大フロー問題を考えれば良さそうです。
こだわり以外のなんでもない話
最後のこだわりとして、最終進化ポケモンおよび進化しないポケモンの中だけから191種類を選出していきます。コレクションは多様性に富んでいてほしいという願いが込められています。
実際のプログラムと結果
pythonで組みました。networkxを用いて最大フロー問題の解析を行っています。実装は以下のJupyter notebookをご覧ください。最下部に結果もあります。
結果の一部を載せます。選ばれし191種類のポケモンに4種類ずつわざを覚えさせることができました。こっそりとニドキングを絶対選出にしています。

さいごに
本記事では、わざをコレクションする問題を考えました。ポケモンとそのポケモンが覚えるわざをもとにネットワークを構成して、最大フロー問題を適用することでわざコレクション問題を解決しました。いくつかのこだわりを入れた改良わざコレクション問題に対してもしっかり最適解を求めることができました。
2022/11/18にはスカーレット・バイオレットが発売されるため、ポケモンやわざも増えるでしょう。データが出揃ってきた段階で、本記事をSV仕様にアップデートする予定です。