学内での勉強会にて、決定木について発表を行いました。
内容は「機械学習クックブック」第14章決定木P227~232まででしたが、今回はレシピ14.01の分類問題について、scikit-learnでの実装とアルゴリズムまとめてみたいと思います。(個人ブログ閉鎖に伴う転載)
scikit-learnでの決定木の実装
まず初めに、sklearnでの決定木の実装を見てみましょう。irisのデータセットを使用し、最後に学習過程を出力しています。
決定木学習用プログラム
import pydotplus
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from IPython.display import Image
from sklearn import tree
# データをロード
iris = datasets.load_iris()
# 説明変数
features = iris.data
# 目的変数
target = iris.target
# 決定木分類器オブジェクトを作成(デフォルトでジニ不純度を不純度指標としている)
decisiontree = DecisionTreeClassifier(random_state=0)
# decisiontree = DecisionTreeClassifier(criterion="entropy", random_state=0)
# 分類器を訓練
model = decisiontree.fit(features, target)
# DOTフォーマットでデータを作成
dot_data = tree.export_graphviz(decisiontree,
out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names)
# グラフを描画
graph = pydotplus.graph_from_dot_data(dot_data)
# グラフを表示
Image(graph.create_png())
決定木の学習過程可視化
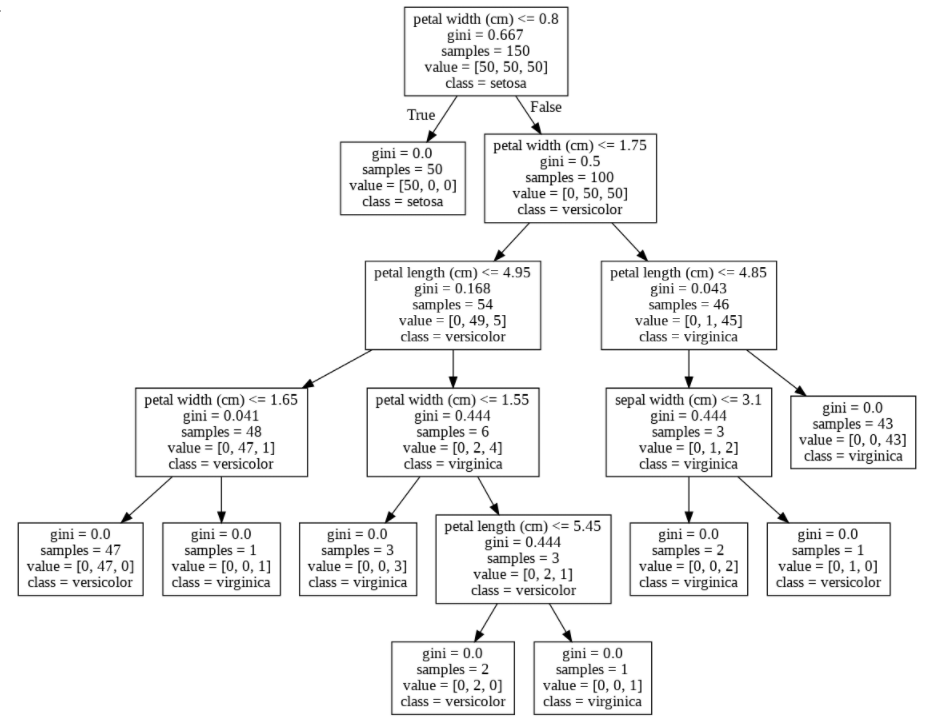
さて、以上のような図が表示されました(諸事情で若干荒い)。まず、この図を解説させて頂くと、この四角で囲まれたもの一つ一つを「ノード」と呼びます。一番上のノード**(根ノード**)について、以下の表のようになっており、その下に続くノードも同じものを示しています。
| 記述 | 記述の説明 |
|---|---|
| petal width(cm) <= 0.8 | 分岐の条件 |
| gini = 0.667 | 今いるノードのジニ不純度 |
| samples = 150 | ノード内の全サンプル数 |
| value = [50, 50, 50] | ノード内の各クラスのサンプル数 (左からsetosa, versicolor, virginica) |
| class = setosa | 「petal width(cm) <= 0.8」のときに最も多くなるクラス名 |
これ以上分割する必要のない(一番下のノード)をリーフと言いますが、そこでは、gini = 0となっていることが分かります。これはノード内のサンプルにばらつきがなく、完全に分類出来ていることを示しています。ジニ不純度についてアルゴリズムと一緒に見ていきます。
決定木のCARTアルゴリズム
まず、scikit-learnの決定木に採用されているアルゴリズムであるCARTについて紹介しようと思います。
CARTとはClassification And Regression Treeの略で、決定木のアルゴリズムの一つです。名前の通り、分類問題と回帰問題の両方を木構造で学習・予測が出来ます。学習の際に、木の分割は2分木で進んでいきます。以下に決定木のアルゴリズムについて簡単にまとめましたものを記載します。
| アルゴリズム | 不純度指標 | 備考 |
|---|---|---|
| ID3 | 分類:情報エントロピー | N分木 ロス・キンラン開発 |
| C4.5 | 〃 | 〃 ID3の改良版 |
| C5.0 | 〃 | 〃 C4.5の改良版 |
| CART | 回帰:MSE, MAEなど 分類:ジニ不純度 or エントロピーなど |
2分木 Leo Breimanら開発 |
それでは、CARTのアルゴリズムについてみていきましょう。今回使う不純度指数はジニ不純度です。情報エントロピーなどについてはまた後日まとめようかと思います。さて、学習の手順は以下のようになっています。
- データを分割する条件を決定(ジニ不純度)
- データを分割する
- 全てのリーフノードが1クラスになるまで木を分割する
1. データを分割する基準を決定(ジニ不純度)
「1.データを分割する条件を決定」では、「○○が20cm以下」といった分割条件を決定します。この分割条件の決定には情報利得を使います。さらにこの情報利得を計算するためにジニ不純度を使います。
ここで行うことは、以下の2つです。
- ジニ不純度の計算
- 情報利得の計算
ジニ不純度とは
ジニ不純度とは、「1つのノード内のデータにあるクラスのばらつき」の指標です。ジニ不純度が大きいほどクラスの分割が出来ておらず、ジニ不純度が小さいほどクラスの分割が出来ているという解釈になります。
定義式は以下のようになります。
$$I_G(t)=\sum^c_{i=1}p(i|t)(1-p(i|t))=1-\sum^c_{i=1}p(i|t)^2$$
ここで、$c$はクラス数,$t$は現在のノード, $p(i|t)$はノード$t$においてクラス$i$に属するサンプルの割合となります。
具体例として、先述したscikit-learnで可視化した決定木の根ノード(一番上のノード)のジニ不純度を実際に計算で求めます。サンプル数は150であり、クラス数は3、各々のクラスには50ずつデータが存在しました。したがって、定義式より、ジニ不純度は
$$I_G(t)=1-(\frac{50}{150})^2-(\frac{50}{150})^2-(\frac{50}{150})^2=1-(\frac{1}{3})^2-(\frac{1}{3})^2-(\frac{1}{3})^2\
=1-\frac{1}{3}=\frac{2}{3}=0.\overline{6}$$
となり、可視化したジニ不純度0.667と一致します。
次の情報利得はこのジニ不純度を用いて計算を行います。
情報利得とは
情報利得は分割の良さを示す指標です。分割前のノードの不純度と分割後の子ノードの不純度の差によって求められます。木の分割が良いほど情報利得は大きくなり、木の分割が悪いほど情報利得は小さくなります。最終目標は情報利得が最大になる条件で木の分割を行うことです。
情報利得(IG)の定義は以下のようになります。
$$IG(D_p,f)=I_G(D_p)-\frac{N_{left}}{N_p}I_G(D_left)-\frac{N_{right}}{Np}I_G(D_{right})$$
ここで、$D_p$は親ノード、$D_{left}$は左子ノード、$D_{right}$は右子ノード、$f$は分割を行う特徴量、$I(D_p)$は親ノード不純度、$N_p$は親ノードのサンプルの数、$N_{left}$は左子ノードのサンプルの個数、$N_{right}$は右子ノードのサンプルの個数となります。
2.データを分割する
「1. データを分割する基準を決定(ジニ不純度)」により、情報利得を最大化するような条件(「○○が20以下」など)が得られたら、その条件でデータを2分木します。
3.全てのリーフノードが1クラスになるまで木を分割する
「1.データを分割する条件を決定」と「2.データを分割する」の処理は、リーフノードが1クラスになる(ジニ不純度が0になる)まで繰り返します。
木の分割を具体例でみる
抽象的な数式だけでは理解が出来ないので、実際に木の分割のための計算をしてみます。今回は以下の例題を考えます。左がパターン1で、右がパターン2です。
まず、親ノードの不純度は
$$I_G(D_p)=1-(0.5^2+0.5^2)=0.5$$
となります。
次に、パターン1での情報利得を考えます。
パターン1の左子ノードの不純度は
$$I_G(D_{left})=1-((\frac{3}{4})^2+(\frac{1}{4})^2)=\frac{3}{8}=0.375$$
パターン1の右子ノードの不純度は
$$I_G(D_{right})=1-((\frac{1}{4})^2+(\frac{3}{4})^2)=\frac{3}{8}=0.375$$
パターン1の情報利得は
$$IG(D_p,f1)=0.5-\frac{4}{8}\times0.375-\frac{4}{8}\times0.375=0.125$$
次に、パターン2での情報利得を考えます。
パターン2の左子ノードの不純度は
$$I_G(D_{left})=1-((\frac{2}{6})^2+(\frac{4}{6})^2)=\frac{4}{9}=0.\overline{4}$$
パターン2の右子ノードの不純度は
$$I_G(D_{right})=1-(1^2+0^2)=0$$
パターン2の情報利得は
$$IG(D_p,f2)=0.5-\frac{6}{8}\times0.\overline{4}-0=0.\overline{16}$$
以上の結果からパターン1の時情報利得0.125、パターン2の時情報利得$0.\overline{16}$より情報利得がより大きいパターン2の方が分割の条件として相応しいということになります。
以上が決定木の分割のアルゴリズムになります。私自身、まだまだ疑問に思うことがあります。機会があればもう少し調査を進めていきたいと思っています。
参考文献
・scikit-learn で決定木分析 (CART 法):
https://pythondatascience.plavox.info/scikit-learn/scikit-learnで決定木分析
・決定木Wiki:
https://ja.wikipedia.org/wiki/決定木
決定木分析についてざっくりまとめ_理論編
https://dev.classmethod.jp/articles/2017ad_20171211_dt-2/
・「達人データサイエンティストによる理論と実践 Python機械学習プログラミング」
・「機械学習クックブック」
・「図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ1冊でしっかりわかる教科書」