IvyFEM(.NET向け有限要素法ライブラリ)をPythonから使用する

1. はじめに

.NET向け有限要素法ライブラリIvyFEM.dllを開発中です。
C#で利用することを想定したライブラリですが、Pythonからも利用できそうなことがわかったので記事にします。

2. Windows10でPythonから.NETを呼び出す方法(Python.NET)

Python.NETを使うことにしました。
http://pythonnet.github.io/

以下、Windows環境にPythonが既にインストールされていることとします。

2.1. Python.NETのインストール

コマンドプロンプトから以下を実行してください。

py -m pip install pythonnet

3. IvyFEM.dllパッケージ

GithubのIvyFEMページから最新のパッケージをダウンロードして、作業ディレクトリに展開してください(IvyFEMページのインストール方法を参照してください、VC++のruntimeが必要）。
IvyFEM: https://github.com/ryujimiya/IvyFEM/

展開すると以下のようになります。

4. PythonからIvyFEMを呼び出す

PythonでPoissonの方程式を解いてみました。

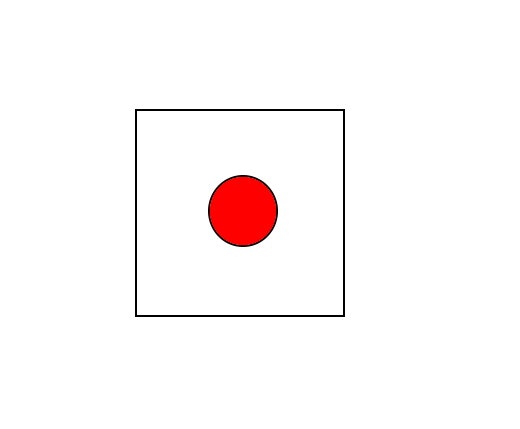
正方形領域をとり、辺上はポテンシャル0の境界条件を課しています。
領域内部に円の領域をとり、その領域に電荷を印加したときの領域全体のポテンシャル分布を計算しています。

main2.py

import clr

clr.AddReference("System")
from System import UInt32

clr.AddReference("System.Collections")
from System.Collections.Generic import List, IList

clr.AddReference('IvyFEM')
from IvyFEM \
import \
Cad2D, Mesher2D, FEWorld, \
FiniteElementType, \
PoissonMaterial, \
CadElementType, FieldValueType, FieldFixedCad, \
Poisson2DFEM

clr.AddReference('IvyFEM')
from IvyFEM.Linear \
import \
LapackEquationSolver, LapackEquationSolverMethod, \
IvyFEMEquationSolver, IvyFEMEquationSolverMethod

clr.AddReference('OpenTK')
from OpenTK import Vector2d

cad = Cad2D()

pts = List[Vector2d]()
pts.Add(Vector2d(0.0, 0.0))
pts.Add(Vector2d(1.0, 0.0))
pts.Add(Vector2d(1.0, 1.0))
pts.Add(Vector2d(0.0, 1.0))
lId1 = cad.AddPolygon(pts).AddLId
print("lId1 = " + str(lId1))

# ソース
lId2 = cad.AddCircle(Vector2d(0.5, 0.5), 0.1, lId1).AddLId
print("lId2 = " + str(lId2))

eLen = 0.05
mesher = Mesher2D(cad, eLen)

# 座標を参照
vecs = mesher.GetVectors()
cnt = len(vecs)
print("len(vecs) = " + str(cnt))
coId = 0
for vec in vecs:
    print("vec[" + str(coId) + "] " + str(vec.X) + ", " + str(vec.Y))
    coId += 1

world = FEWorld()
world.Mesh = mesher

dof = 1 # スカラー
feOrder = 1
quantityId = world.AddQuantity(dof, feOrder, FiniteElementType.ScalarLagrange)

world.ClearMaterial()
ma1 = PoissonMaterial()
ma1.Alpha = 1.0
ma1.F = 0.0
ma2 = PoissonMaterial()
ma2.Alpha = 1.0
ma2.F = 100.0
maId1 = world.AddMaterial(ma1)
maId2 = world.AddMaterial(ma2)

lId1 = 1
world.SetCadLoopMaterial(lId1, maId1)

lId2 = 2
world.SetCadLoopMaterial(lId2, maId2)

zeroEIds = [1, 2, 3, 4]
zeroFixedCads = List[FieldFixedCad]()
for eId in zeroEIds:
    #スカラー
    # オーバーロードであることに注意
    fixedCad = FieldFixedCad.Overloads[UInt32, CadElementType, FieldValueType](eId, CadElementType.Edge, FieldValueType.Scalar)
    zeroFixedCads.Add(fixedCad)
world.SetZeroFieldFixedCads(quantityId, zeroFixedCads)

#DEBUG
zeroFixedCads = world.GetZeroFieldFixedCads(quantityId)
print("len(zeroFixedCads) = " + str(len(zeroFixedCads)))

world.MakeElements()

feIds = world.GetTriangleFEIds(quantityId)
feCnt = len(feIds)
print("feCnt = " + str(feCnt))
for feId in feIds:
    print("--------------")
    print("feId = " + str(feId))
    triFE = world.GetTriangleFE(quantityId, feId)
    nodeCoIds = triFE.NodeCoordIds
    elemNodeCnt = nodeCoIds.Length
    for iNode in range(elemNodeCnt):
        print("coId[" + str(iNode) + "] = " + str(nodeCoIds[iNode]))

# ポアソン方程式FEM
FEM = Poisson2DFEM(world)

# リニアソルバー
'''
solver = LapackEquationSolver()
solver.IsOrderingToBandMatrix = True
solver.Method = LapackEquationSolverMethod.Band
FEM.Solver = solver
'''

solver = IvyFEMEquationSolver()
solver.Method = IvyFEMEquationSolverMethod.NoPreconCG
FEM.Solver = solver

# 解く
FEM.Solve()
U = FEM.U

# 結果
nodeCnt = len(U)
for nodeId in range(nodeCnt):
    print("-------------")
    coId = world.Node2Coord(quantityId, nodeId)
    value = U[nodeId]
    print(str(nodeId) + " " + str(coId) + " " + "{0:e}".format(value))

5. 実行

py -m main2

5. まとめ

IvyFEM.dllを使ってPythonからPoissonの方程式を解きました。