More than 3 years have passed since last update.

論文読み.1 Learning Wasserstein Embeddings

Last updated at 2020-05-18Posted at 2020-03-31

はじめに

Learning Wasserstein Embeddingsという論文を読んだのでまとめていきます。

1. 対象とするトピック

1.1 キーワード

Wasserstein distance 論文

1.2 経緯

Wasserstein distanceとは、「物質をある場所から他の場所へ最小費用で移す」理論である最適輸送理論から導かれる距離関数です。より詳細には最適輸送理論問題は(平たく言うと)確率測度空間上の変分問題に相当し、この変分問題の特殊な場合にWasserstein distanceという確率測度空間上の距離関数が導かれます。参考
　論文ではp-Wasserstein distanceが以下のように定式化されています。

距離空間X上での距離をd_Xとする。 \\
p \in (0, \infty) となるpに対しP_p(X)をX上での全てのBorel確率測度\muの空間とする。 \\
このとき、\muと\nuとのp-Wasserstein distanceは以下の数式で定義される。 \\
W_p(\mu, \nu) = (inf_{\pi \in \Pi(\mu, \nu)}\int\int_{X \times X}d(x, y)^pd \pi(x, y))^{\frac{1}{p}}

　このWasserstein distanceがWasserstein GAN [arxiv] (https://arxiv.org/pdf/1701.07875.pdf)の登場により分布間の距離を表すものとして注目されてきました。

1.3 応用例

　機械学習では以下の分野で利用されています。

[ドメイン適応] (https://arxiv.org/abs/1507.00504)
[単語の埋め込み] (https://papers.nips.cc/paper/6139-supervised-word-movers-distance.pdf)

2. 問題点

Wasserstein distanceは計算コストが大きく(計算量は3乗オーダー)、用途が限定されています。

3. 解決策

　上述の問題を踏まえ、Wasserstein distance固有の複雑さを解消する近似手法を提案することが本論文で提案する解決策です。

4. 手法

4.1 概要

　Euclidean normがWasserstein distanceの近似となるような分布のEuclidean embeddingを学習します。この手法により、埋め込まれた空間上でもユークリッド空間上での手法を用いることができます。また、計算時間を大幅に削減することができます。

4.2 理論

4.2.1 DWE

　学習においては深層学習を用います。入力はd次元ヒストグラムの組

\{x_{i}^{1}, x_{i}^{2}\}_{i \in 1,...,n}

とそれに対応するWasserstein distance

\{y_i = W_{2}^{2}(x_{i}^{1}, x_{i}^{2})\}_{i \in 1,...,n}

です。
　ナイーブな手法としてはサンプル1, 2を連結しyを学習するという手法が考えられます。しかしこの手法はWasserstein distanceの重要な特徴である対称性が失われてしまいます。そこでこの対称性も上手くエンコードできるように別の手法を論文では採用しています。具体的にはSiamese neural networkというネットワークを用います。元々は距離学習で用いられる手法で、同じ学習データセットから二つをサンプルし入力とした後に新たな空間へと写像する関数を学習します。
　この論文ではSiamese neural networkに基づいた提案手法をDeep Wasserstein Embedding (DWE)と呼称しています。以降ではDWEについて説明します。

4.2.1.1 概念

　DWEでは入力されたヒストグラムをp次元のユークリッド空間に射影する埋め込み用のネットワークを学習します。また、デコーダー用のネットワークも学習します。このデコーダーを用いることでネットワークの解釈が可能になります。DWE全体のアーキテクチャは以下の図の通りです。

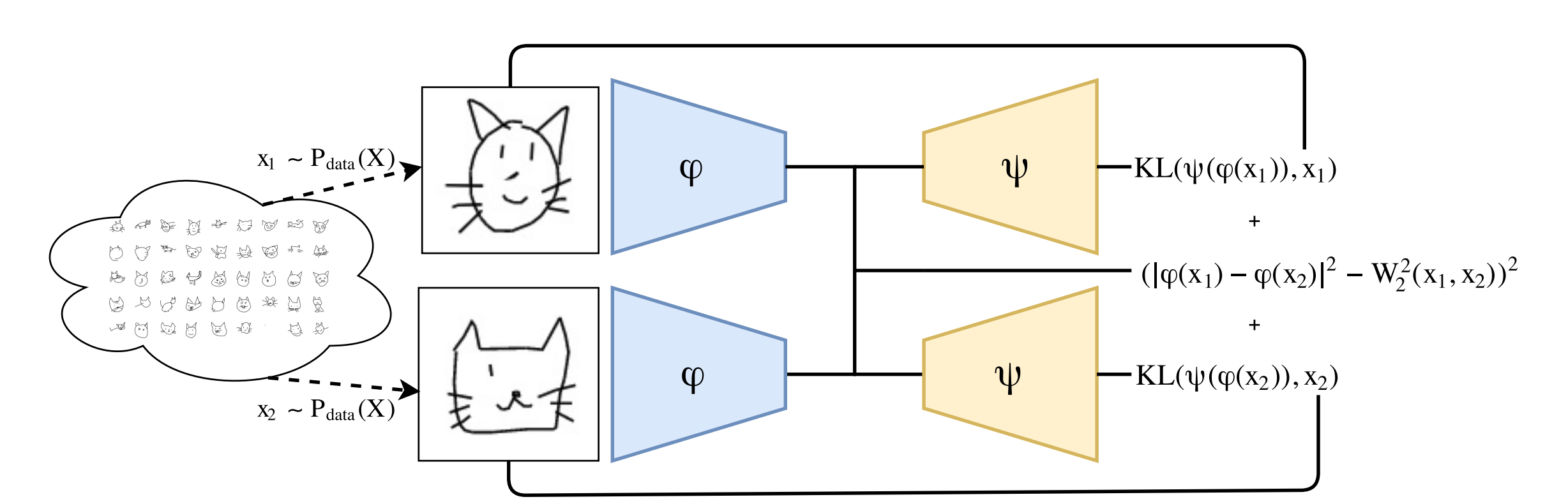
　学習は埋め込まれた状態でのsquared Euclidean distanceがWasserstein distanceと近づくように行われます。また、デコーダーはKullback-Leibler divergence lossを損失として用いて学習を行なっています。Kullback-Leibler divergenceは確率分布間の距離を計算する際によく用いられます。論文ではWasserstein metricの演算が確率分布上で行われることに基づいてKullback-Leibler divergenceを損失として用いることにしたと記載されています。
　目的関数は以下の数式で表されています。最初のシグマ計算の項はエンコーダーで変換されたデータ (特徴量ベクトル)間でのEuclid distanceと入力された画像データに対してあらかじめ計算されているWasserstein distanceの二乗誤差を表しています。また、以降の項ではデコーダーで再構成されたデータと入力されたデータ間でのKullback-Leibler divergenceを表しています。λとΣは両方のKL項にかかっているので注意してください (元論文の表記をそのまま使用しています)。両者が小さくなることで特徴量ベクトルのEuclid distanceを計算するとWasserstein distanceを近似した結果が出るエンコーダーと、性能の良い (Kullback-Leibler divergenceが小さい)デコーダーを構築することが出来るという目的関数になっています。

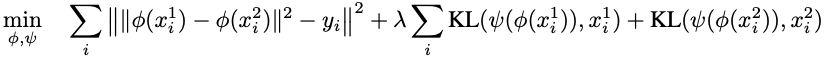
4.2.1.2 コード

　実際にコードを確認してみます。modelの生成を行なっているコードから一部抜粋してみます。

def build_model(image_shape=(28,28), embedding_size=50):

    s = image_shape[-1]
    feat=Sequential()
    feat.add(Conv2D(20,(3,3),
            activation='relu',padding='same',
            input_shape=(1, s, s), data_format='channels_first'))
    feat.add(Conv2D(5,(5,5),activation='relu',data_format='channels_first', padding='same'))
    feat.add(Flatten())
    feat.add(Dense(100))
    feat.add(Dense(embedding_size))

    inp1=Input(shape=(1,s,s))
    inp2=Input(shape=(1,s,s))

    feat1=feat(inp1)
    feat2=feat(inp2)

    distance = Lambda(euclidean_distance,
                      output_shape=eucl_dist_output_shape)([feat1, feat2])

    feat.compile('sgd','mse')
    model=Model([inp1,inp2],distance)
    model.compile('adam','mse')

    unfeat=Sequential()
    input_dim = feat.get_output_shape_at(0)[-1]
    unfeat.add(Dense(100, input_shape=(input_dim,), activation='relu'))
    unfeat.add(Dense(5*s*s, activation='relu'))
    unfeat.add(Reshape((5, s,s)))
    unfeat.add(Conv2D(10,(5,5),activation='relu',data_format='channels_first', padding='same'))
    unfeat.add(Conv2D(1,(3,3),activation='linear',data_format='channels_first', padding='same'))
    unfeat.add(Flatten())
    unfeat.add(Activation('softmax')) # samples are probabilities
    unfeat.add(Reshape((1,s,s)))


    uf1=unfeat(feat1)
    uf2=unfeat(feat2)

    unfeat.compile('adam','kullback_leibler_divergence')

    model2=Model([inp1,inp2],[distance, uf1,uf2, uf1, uf2])
    model2.compile('adam',['mse', kullback_leibler_divergence_,kullback_leibler_divergence_,
                           sparsity_constraint, sparsity_constraint],
                           loss_weights=[1, 1e1,1e1, 1e-3, 1e-3])

    return {'feat':feat, 'emd':model,'unfeat':unfeat,'dwe':model2}

　若干長いので簡潔に日本語でまとめてみます。まず、ネットワーク全体としてはEncoder-Decoderの構造を取っています。そして、処理の流れは以下の通りです。

エンコーダーで２つの画像データからそれぞれ特徴量ベクトルを抽出する (feat)
抽出した特徴量ベクトル間でのEuclid distanceを計算する
デコーダーで抽出した特徴量ベクトルからそれぞれ画像データを再構成する (unfeat)
再構成された画像データとそれに対応した、入力として与えられた画像データ間でKullback-Leibler divergenceを計算する。
　なお、1と2の処理をまとめてemd、3と4の処理をまとめてdweと呼称しているようです。

4.2.2 Wasserstein Data Mining in the Embedded Space

　前節で述べた一般的な理論だけでなく、既存手法への適応も紹介されています。以下に列挙します。

4.2.2.1 Wasserstein barycenters

　Euclid spaceと同様に、Wasserstein spaceでも重心は距離(Wasserstein distances)の総和が最小となる点として定義されます。提案手法を用いると以下のように近似できます。

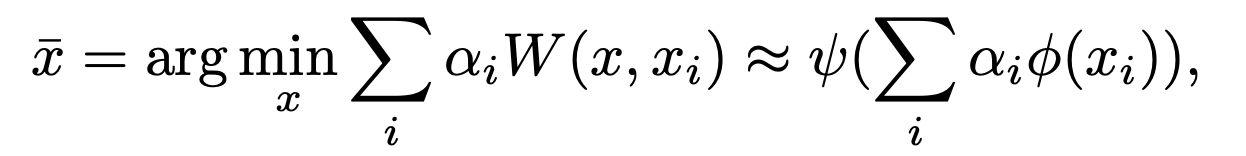
vは埋め込まれた空間の次元数を表しており、上記の更新式によって再帰的に定義されます。

4.2.2.2 Principal Geodesic Analysis in Wasserstein space`

　Principal Geodesic Analysis (PGA)は一般リーマン多様体上でのPCAを一般化した手法です。PCAと同様に、データの統計的多様性が最大となるエンコードを行う主測地線を求めます。手法を適応した場合、以下の最大化問題に帰着します。

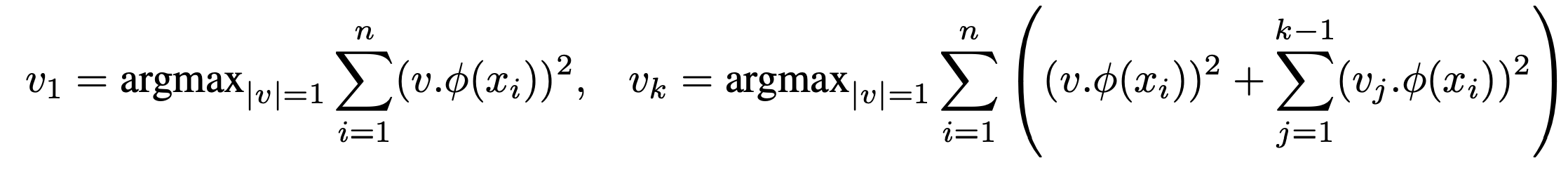
5. 実験

　グレースケール画像に対して実験を行っています。詳細な条件や設定は割愛します。使用したデータセットは以下二つです。

MNIST (お馴染みの手書き文字)
Google Doodle (マウスで描かれた手描きの絵)
　MNISTについて実験結果をまとめます。最初に行なっていたのは計算時間の評価です。結果は以下の図の通りです。

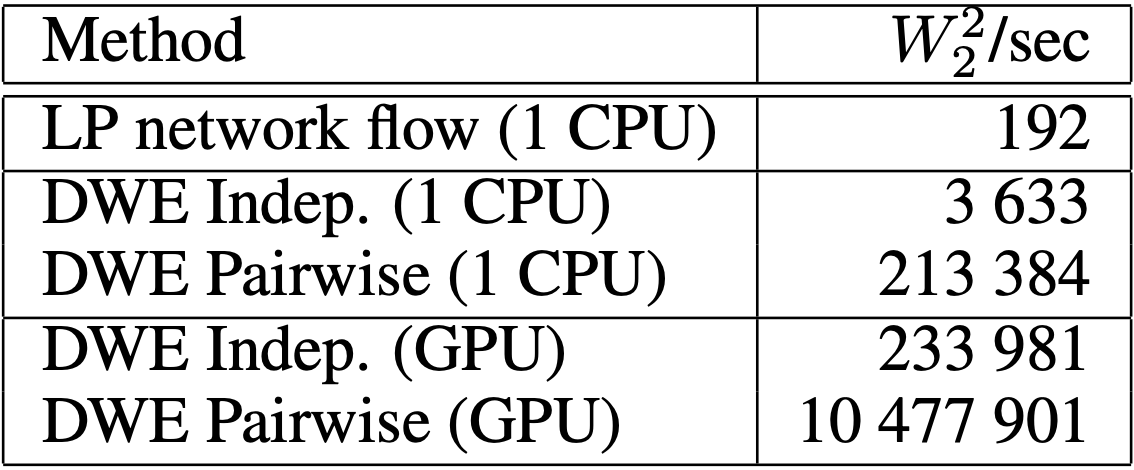　DWEを用いることで距離計算の速度が向上していることが分かります。

　次に埋め込みの性能を評価しています。重心計算とPGAを可視化し、その鮮明さによって評価を行なっています。重心計算の可視化結果は以下のようになります。

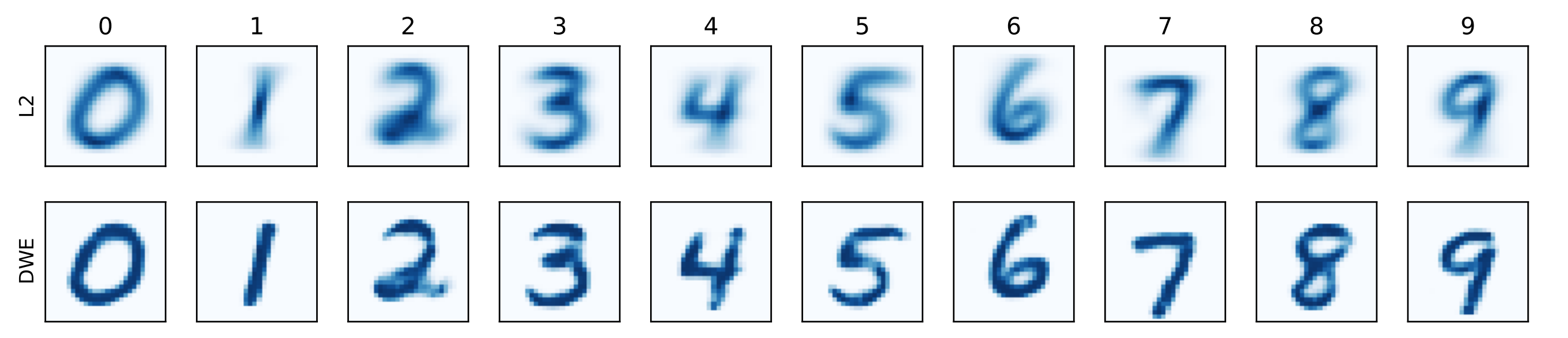
　また、PGAの可視化結果は以下のようになります。

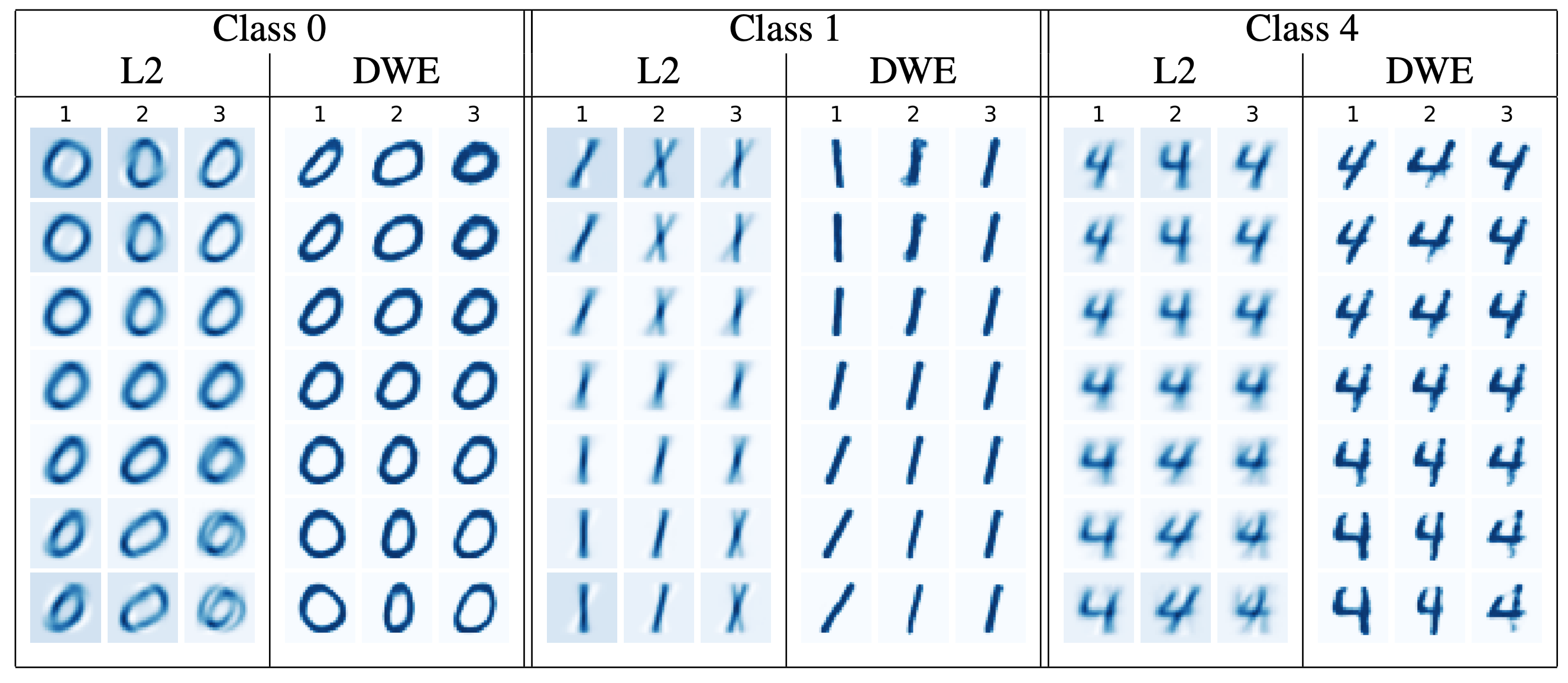
　共に、DWEを用いることでより鮮明な可視化ができています。先行研究によると、鮮明さが評価において重要であり、今回はその理屈に基づき鮮明さを評価基準としているようです。

6. 問題点

　論文では理論的な裏付けと近似の性能においていくつか未解決な点があると言及されています。以下に列挙します。

ネットワークが良い埋め込みを学習するために十分な構成になっているのかが予測しにくい。
Wasserstein embeddingについての理論的な裏付けが不十分である。今回は実験的に有用性を証明しただけで理論的な証明はできていない。

終わりに

　実験において統計量による評価が少なかった点と、Kullback-Leibler divergenceを使う正当性について気になりました。今後も論文をまとめていこうと思います。

参考文献

PROCRASIST (2017), 【Day-23】機械学習で使う"距離"や"空間"をまとめてみた, https://www.procrasist.com/entry/23-distance
Nicolas Courty, Remi Flamary, Melanie Ducoffe (2018), LEARNING WASSERSTEIN EMBEDDINGS, https://openreview.net/pdf?id=SJyEH91A-
Asuka TAKATSU (2014), 最適輸送理論梗概, http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1916-11.pdf
Martin Arjovsky, Soumith Chintala, Leon Bottou (2017), Wasserstein GAN, https://arxiv.org/abs/1701.07875
J. Solomon, F. de Goes, G. Peyré, M. Cuturi, A. Butscher, A. Nguyen, T. Du, and L. Guibas (2015), Convolutional wasserstein distances: Efficient optimal transportation on geometric domains
ryuji0123 (2020), 論文読み. 5 Martin Arjovsky, Soumith Chintala, and L´eon Bottou. Wasserstein Generative Adversarial Networks (PMLR 2017), https://qiita.com/ryuji0123/items/5f14552969299ab7e31e

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up