Strawberry Fieldsで光量子計算をする(その8) Gaussian Wigner function

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

前置き

今回はWigner関数によるガウス状態の取り扱いを少し詳しく紹介します。

この記事で、光連続量量子計算における状態には

• ガウス状態
• 非ガウス状態

の2通りがあると書きました。

また状態の記述の仕方にも

• 光子数基底
• Wigner関数

の2通りがあります。
(光子数基底で記述した状態をWigner関数で描写したりもするので正確な表現ではない気もしますが、ここではスルーします)
今回注目するのは ガウス状態 と Wigner関数 の組合わせです。

Wigner関数の基本

Wigner関数は直交位相$x, p$を変数とした、量子状態の確率分布関数にあたります。
一般に以下の式で表されます。

W(x, p) = \frac{2}{\pi} \int dy e^{4iyp} \bra{x-y}\hat{\rho}\ket{x+y}

$\hat{\rho}$は状態の密度演算子です。
確率分布関数的な性質として、以下の式が成り立ちます。

$\alpha = x + ip$として、

• 全空間における積分値が1 = 確率の総和が1
  $$
  \int W(\alpha)d^2 \alpha = 1
  $$

• $x, p$それぞれについて周辺分布をとることが可能
  $$
  \int W(x, p)dx = \bra{p}\hat{\rho}\ket{p}
  $$

$$
\int W(x, p)dp = \bra{x}\hat{\rho}\ket{x}
$$

• ある状態における演算子$\hat{A}$の期待値を記述可能

$$
\left< \hat{A}\right> = \mathrm{Tr} (\hat{\rho}\hat{A}) = \int W(\alpha)A(\alpha)d^2 \alpha
$$

ただし、Wigner関数は古典的な確率分布と異なり負の値をとることがあります。
(シュレーディンガーの猫状態など)

では早速このWigner関数を使って任意の量子状態を計算してみましょう、
と言いたいところですがちょっと難しいです。それは今度にして、今回はガウス状態に対象を絞ります。

Gaussian Wigner function

実は、ガウス状態に限定するとWigner関数はもっと簡単な形に書けます。
これが今回のサブタイトルとしたGaussian Wigner functionです。

$$
W(\xi) = \frac{1}{(2\pi)^{N} \sqrt{\det V^{(N)}}} \exp{\left( -\frac{1}{2}\xi [V^{(N)}]^{-1} \xi^{T} \right)}
$$

$\xi = [x_{1}, p_{1}, x_{2}, p_{2}, \dots, x_{N}, p_{N}]$には$N$個のqumodeの直交位相が埋め込まれています。
$V^{(N)}$は$2N \times 2N$の共分散行列です。
見ての通り、古典的なガウス分布とよく似ています。
この関数を直交位相平面(x, p)上で計算しプロットすることで、直交位相状態の確率分布が視覚的にわかります。

計算方法ですが、古典的なガウス分布分布がそうであるように、Gaussian Wigner functionも1次と2次のモーメント(平均と分散)でパラメタライズされます。
よって、ゲート演算は平均と共分散行列の値を操作します。

ただし平均は$\xi \to \xi - \mu$の置き換えで済むため、主に考える必要があるのは共分散行列に対する操作です。

ゲート演算

基本的には、直交位相$\hat{x}, \hat{p}$へのゲート操作を表す行列を共分散行列にかけていくだけです。

ただし知っておくべきこととして、演算の前後で直交位相における交換関係$[\hat{x_k}, \hat{p_{l}}] = \frac{i}{2}\delta_{k l}$ (係数は規格化済)を満たしている必要があります。
この交換関係を一般化すると以下のように書けます。

$$
[\hat{\xi_k}, \hat{\xi_l}] = \frac{i}{2} \Lambda_{kl}
$$

\Lambda = \oplus_{i=1}^{N}J
\\
J = 
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix}

$\Lambda$を表すのに使用している記号は直和です。
例えば$N=2$の場合、以下のようになります。

\Lambda = 
\begin{pmatrix}
J & 0 \\
0 & J
\end{pmatrix}

この交換関係を保存するような変換行列$S$は、以下の関係を満たす必要があります。

$$
S \Lambda S^T = \Lambda
$$

このような$S$をsymplectic matrix (斜交行列)と呼びます。
また以下のような変換をsymplectic transformationと呼びます。

$$
V^{(N)} \to V^{(N)'} = S V^{(N)} S^T
$$

Gaussian Wigner functionの共分散行列に対して実行可能な変換はsymplectic transformationです。
主なガウス操作はDisplacement gate, Squeezing gate, Rotation gate, Beam splitterですが、平均に対する操作であるDisplacement gateを除いてsymplectic transformationになっています。

例として$N=1$の場合、

\Lambda = 
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix}

S = 
\begin{pmatrix}
e^{-r} & 0 \\
0 & e^{r}
\end{pmatrix}\ \ \ :Squeezing\ Gate

で計算すると$S \Lambda S^T = \Lambda$が示せます。

multi qumodesにも拡張可能で、$N=2$で0番目のqumodeのみをスクイーズする場合は以下の行列で同様の計算をします。

\Lambda = 
\begin{pmatrix}
0 & 1 & 0 & 0 \\
-1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & -1 & 0 \\
\end{pmatrix}

S = 
\begin{pmatrix}
e^{-r} & 0 & 0 & 0 \\
0 & e^{r} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}

各ゲート行列の解説はこちらが詳しいです。ただし生成・消滅演算子で書かれているため直交位相を用いた表記に変換が必要です。

実装してみた

例によって最低限の機能で素朴に実装してみました。
まずGaussian Wigner Transformationを行うためのクラスを作ります。

import numpy as np
import numpy.linalg
import matplotlib.pyplot as plt

class Gaussian_trans():
    def __init__(self, N):
        self.N = N # num of qubit
        self.V = np.eye(2 * N)
        self.mu = np.zeros(2 * N)
        #self.V = []
        #for i in range(N):
         #   self.V.append(np.eye(2))
        #self.V = np.array(self.V)
        
    def Xsqueeze(self, idx, r):
        idx = 2 * idx
        S = np.eye(2 * self.N)
        S[idx:idx+2, idx:idx+2] = np.array([[np.exp(-r), 0], [0, np.exp(r)]])
        self.V = np.dot(S, np.dot(self.V, S.T))
        self.mu = np.dot(S, self.mu)
        
    def Psqueeze(self, idx, r):
        idx = 2 * idx
        S = np.eye(2 * self.N)
        S[idx:idx+2, idx:idx+2] = np.array([[np.exp(r), 0], [0, np.exp(-r)]])
        self.V = np.dot(S, np.dot(self.V, S.T))
        self.mu = np.dot(S, self.mu)
        
    def rotation(self, idx, theta):
        idx = 2 * idx
        S = np.eye(2 * self.N)
        S[idx:idx+2, idx:idx+2] = np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]])
        self.V = np.dot(S, np.dot(self.V, S.T))
        self.mu = np.dot(S, self.mu)
        
    def BS(self, idx1, idx2, theta):
        idx1 = 2 * idx1
        idx2 = 2 * idx2
        S = np.eye(2 * self.N)
        S[idx1:idx1+2, idx1:idx1+2] = np.array([[np.sin(theta), 0], [0, np.sin(theta)]])
        S[idx1:idx1+2, idx2:idx2+2] = np.array([[np.cos(theta), 0], [0, np.cos(theta)]])
        S[idx2:idx2+2, idx1:idx1+2] = np.array([[np.cos(theta), 0], [0, np.cos(theta)]])
        S[idx2:idx2+2, idx2:idx2+2] = np.array([[-np.sin(theta), 0], [0, -np.sin(theta)]])
        self.V = np.dot(S, np.dot(self.V, S.T))
        self.mu = np.dot(S, self.mu)
    
    def Displace(self, idx, x, p):
        self.mu[idx:idx+2] = self.mu[idx:idx+2] + np.array([x, p]) * 2
    
    def GaussianWigner(self, xi, V, mu):
        xi = xi - mu
        xi_tmp = np.ravel(xi)
        N = np.int(len(xi_tmp) / 2)
        det_V = np.linalg.det(V)
        V_inv = np.linalg.inv(V)
        W = (2 * np.pi)**(-N) / np.sqrt(det_V) * np.exp(-1/2 * np.dot(xi_tmp, np.dot(V_inv, xi_tmp.T)))
        return W

    def plotGaussianWigner(self, idx):
        idx = idx * 2
        x = np.arange(-5, 5, 0.1)
        p = np.arange(-5, 5, 0.1)
        m = len(x)
        xx, pp = np.meshgrid(x, p)
        xi_array = np.dstack((pp, xx))
        W = np.zeros((m, m))
        for i in range(m):
            for j in range(m):
                W[i][j] = self.GaussianWigner(xi_array[j][i], self.V[idx:idx+2, idx:idx+2], self.mu[idx:idx+2])
        h = plt.contourf(x, p, W)
        plt.show()

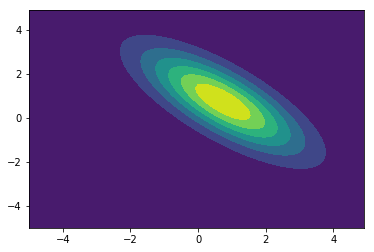
下記の通り操作を実行し、プロットします。

G = Gaussian_trans(2) # two qumode [0, 1]
G.Displace(0, 2, 0) # Displacement gate, x to x+2
G.Xsqueeze(0, 1) # X squeeIng gate, r=1
G.rotation(0, np.pi/4) # pi/4 rotation gate
G.BS(0, 1, np.pi/4) # 50:50 beam splitter
G.plotGaussianWigner(0) # plot
print('mu0 =', G.mu[0:2]) # mu of qumode 0
print('mu1 =', G.mu[2:4]) # mu of qumode 1

実行結果は以下の通りです。

mu0 = [0.73575888 0.73575888]
mu1 = [0.73575888 0.73575888]

上記コードは以下のStrawberry fieldsコードと同じ結果を返しています。

import strawberryfields as sf
from strawberryfields.ops import *

eng, q = sf.Engine(2)

with eng:
    # prepare the initial states
    Dgate(2) | q[0] # displacement gate
    Sgate(1) | q[0] # position squeezed
    Rgate(pi/4) | q[0] # rotation gate
    BSgate(pi/4, 0) | (q[0], q[1])  # 50-50 beamsplitter
    
    # perform the homodyne measurements
    #MeasureX | q[1]   

state = eng.run('gaussian')
mu0, cov0 = state.reduced_gaussian([0])
mu1, cov1 = state.reduced_gaussian([1])
print('mu0 =', mu0)
print('mu1 =', mu1)

x = np.arange(-5, 5, 0.1)
p = np.arange(-5, 5, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
plt.contourf(X, P, W)

Strawberry fieldsでの内部実装はもうひと工夫されているようです。
Williamson decompositionという手法によって共分散行列をsymplectic行列と対角行列に分解して保持しているとあります。

まとめ

Gaussian Wigner functionをベースとしたガウス操作の計算について確認しました。
忘れてはならないのは、ガウス操作だけではユニバーサルな量子計算には不十分です。
実際、Gaussian Wigner functionのパラメータ数はqumode数Nに対し多項式関数(共分散と平均で$4N^2 + 2N$)で、古典計算で効率的にシミュレートできてしまいます。

ただし、ガウス操作と他の様々なリソース(測定やフィードフォワード、確率的非ガウス状態)の組み合わせでユニバーサル量子計算を行う試みは今後も続くと考えられるため理解しておいて損はないと思います。

以上、最後までありがとうございました。

参考にした文献

• Akira Furusawa, Peter van Loock, "Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing", WILEY
• https://arxiv.org/abs/quant-ph/0410100v1