$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
前書き
今回は"シュレーディンガーの猫状態"(あるいは単に猫状態:Cat state)を見ていきたいと思います。
"シュレーディンガーの猫"は、量子力学的な重ね合わせ状態がマクロな事象に許されるとしたら奇妙な事になるぞ、という事を表す有名な思考実験です。
Cat stateはその思考実験を由来として名付けられた非古典的な状態です。
特徴として、ウィグナー関数が局所的に負の値を取ります。これは古典的な状態ではあり得ない、純粋に量子力学的な特徴です。
また、次あたりに扱おうと考えているGKP符号の生成にも使えるようです。
GKP符号は量子誤り訂正符号の中でbosonic codeと呼ばれるものの1種です。
量子力学的な調和振動子に符号を埋め込み、論理qubitとして使用します。
Cat stateの定式
Cat stateの定義は以下の通りです[1]。
\ket{cat} = \frac{e^{-|\alpha|^2/2}}{\sqrt{2(1\pm e^{-2|\alpha|^2} )}}(\ket{\alpha} \pm \ket{-\alpha})
$\ket{\alpha}$はコヒーレント状態です。
Cat stateは2つの(位相が反転した)コヒーレント状態の量子力学的な重ね合わせ状態です。
$\pm$の符号がプラスの場合"even cat state"、マイナスの場合"odd cat state"と呼ばれます。
コヒーレント状態は量子状態として記述できますが、準古典状態と言われ古典的なレーザー光でよく近似されます。
ほぼ古典光であるコヒーレント光が量子力学的に重ね合わされている、と考えるとシュレーディンガーの猫と近い不思議さが感じられますね。
コヒーレント状態は、Gaussian Wigner functionをベースとした計算では直交位相平面上でVacuum stateに対しDisplacement operatorを作用させた状態でした。
光子数基底では以下のように表します。
\ket{\alpha} = e^{-\frac{|\alpha|^2}{2}} \sum^{\infty}_{n=0} \frac{\alpha^{n}}{\sqrt{n!}}\ket{n}
無限の光子数状態の重ね合わせです。
$\ket{n}$の係数は、光子数測定時に光子数nが得られる確率振幅に対応します。
\ket{-\alpha} = e^{-\frac{|\alpha|^2}{2}} \sum^{\infty}_{n=0} \frac{(-1)^n\alpha^{n}}{\sqrt{n!}}\ket{n}
となるため、even cat stateは$n$が偶数の光子数基底のみ打ち消されず残ります。
odd cat stateはその逆です。不思議な状態ですね。
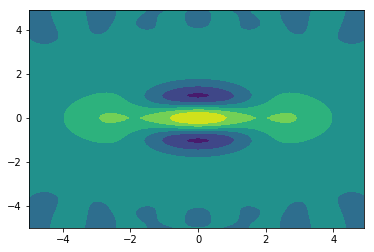
Strawberry Fieldsはbuilt inのcat stateが用意されているので、プロットしてみましょう。
eng, q = sf.Engine(1)
alpha = 2
p = 0 # 0: even, 1: odd
with eng:
Catstate(alpha = alpha, p = p) | q[0]
state = eng.run('fock', cutoff_dim=50)
lim = 5
x = np.arange(-1*lim, lim, 0.05)
p = np.arange(-1*lim, lim, 0.05)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
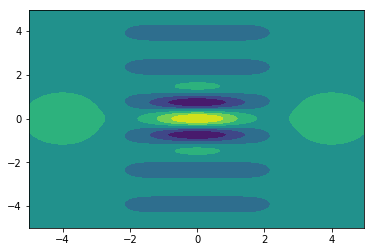
plt.contourf(X, P, W)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X, P, W, cmap='bwr', linewidth=0)
fig.colorbar(surf)
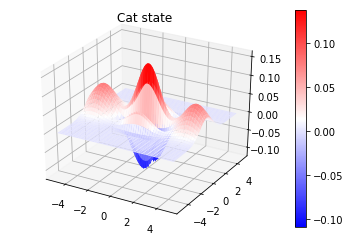
ax.set_title("Cat state")
fig.show()
ウェグナー関数が干渉縞のように波打っており、かつ負の部分が存在することがわかります。
Cat stateの生成法
色々考えられているようです。
最新ではないかもですが、この論文がいい感じにまとまっていました。
いくつか紹介してみます。
正攻法っぽいのはcross-Kerr nonlinearityと呼ばれる非線形効果を利用する方法。
相互作用ハミルトニアンは以下の通りです。$\chi$は非線形性の強さを表すパラメータです。
$$
H = \hbar \chi \hat{a_1}^\dagger\hat{a_1}\hat{a_2}^\dagger\hat{a_2}
$$
$\ket{0}, \ket{1}$の重ね合わせ状態とコヒーレント状態をこの相互作用ハミルトニアンのもと時間発展させると、
e^{iHt/\hbar} \frac{1}{\sqrt{2}} (\ket{0}_1 + \ket{1}_1)\ket{\alpha}_{2} \\
= \frac{1}{\sqrt{2}} (\ket{0}_1 \ket{\alpha}_{2} + \ket{1}_1 \ket{\alpha e^{i\chi t}}_{2})
$\chi t = \pi$となるようパラメータは調節します。
mode 1をsuperposed basis $\frac{1}{\sqrt{2}} (\ket{0}_1 \pm \ket{1}_1)$で測定すれば、測定結果に応じてeven/odd cat stateがmode 2に残ります。
(superposed basisでの測定はこちらを参考に)
以下、Strawberry Fieldsコードです。
import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import scale
from numpy import pi, sqrt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
eng, q = sf.Engine(3)
alpha = 1
kappa = np.pi
with eng:
Fock(1) | q[0]
Vacuum() | q[1]
Coherent(alpha) | q[2]
BSgate(np.pi / 4) | q[0:2]
CKgate(kappa) | q[1:3]
BSgate(np.pi / 4) | [q[0], q[1]]
MeasureFock(select = 1) | q[1]
#MeasureFock(select = 1) | q[0]
state = eng.run('fock', cutoff_dim=10)
lim = 5
x = np.arange(-1*lim, lim, 0.1)
p = np.arange(-1*lim, lim, 0.1)
W = state.wigner(2, x, p)
X, P = np.meshgrid(x, p)
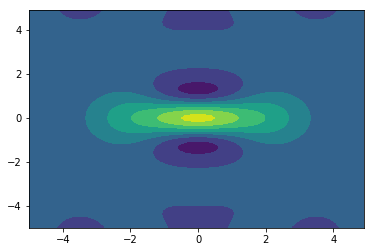
plt.contourf(X, P, W)
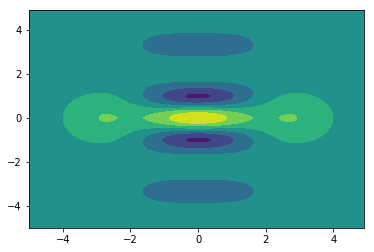
出力の確認ですが、Strawberry Fieldsでbuilt inのcat stateを使います。
上のコードと同じcat stateを出力し、一致することを確認しましょう。
eng, q = sf.Engine(1)
with eng:
Catstate(alpha = 1, p = 0) | q[0]
state = eng.run('fock', cutoff_dim=10)
lim = 5
x = np.arange(-1*lim, lim, 0.1)
p = np.arange(-1*lim, lim, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
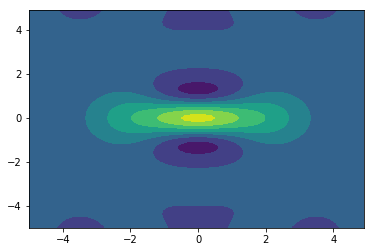
plt.contourf(X, P, W)
できてそうですね。
この方法の問題点は、実在する物質で$\chi t = \pi$を実現するのが"extremely difficult"なことです。ほぼ無理です。
なので少しでもハードルを下げようと研究された方法も、同論文では紹介されています。
1つ挙げると、以下の二段構えです。
- 比較的小さい($\alpha \leq 1.2$)cat stateはsingle photon stateに対しsqueezeを行うことで良く近似できる。
- シンプルな系を用いて、複数の小さなcat stateからより大きなcat stateが作れる。
single photon stateもsqueezing geteも楽じゃないと思いますけど、多分マシです、
より具体的なメソッドはこちらのp.6、さらに詳細はこちらに載っています。
以下にStrawberry Fieldsでの実行コードを載せます。
eng, q = sf.Engine(3)
s = - 0.313 # squeezing parameter
# When <squeezing parameter = -0.313>, squeezed single photon states approximately become cat states with <amplitude = 1>
alpha = 1
beta = 1
gamma = 2 * alpha * beta / np.sqrt(alpha**2 + beta**2)
theta = np.arctan(alpha / beta)
with eng:
# produce approximated odd cat states (squeezed single photon states)
Fock(1) | q[0]
Sgate(s) | q[0]
Fock(1) | q[1]
Sgate(s) | q[1]
# prepare coherent state
Coherent(gamma) | q[2]
# interaction
BSgate(theta) | q[0:2]
BSgate(np.pi / 4) | q[1:3]
# conditional measurement
MeasureHomodyne(0, select = np.real(alpha)) | q[1]
MeasureHomodyne(0, select = -np.real(alpha)) | q[2]
state = eng.run('fock', cutoff_dim=20)
lim = 5
x = np.arange(-1*lim, lim, 0.1)
p = np.arange(-1*lim, lim, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
plt.contourf(X, P, W)
上記コードと比較確認用にbuilt inのcat stateを生成し、プロットします。
eng, q = sf.Engine(1)
with eng:
Catstate(alpha = np.sqrt(2)) | q[0]
state = eng.run('fock', cutoff_dim=20)
lim = 5
x = np.arange(-1*lim, lim, 0.1)
p = np.arange(-1*lim, lim, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
plt.contourf(X, P, W)
大体同じですね。
シミュレータとはいえ、論文で紹介されている方法がきちんと機能して見えるのは愉快です。
ただ、Fock backendは調子に乗ってcutoff_dimを挙げると容易にカーネルが死にます。
古典計算機のつらみですね。
まとめ
Strawberry Fieldsを使い、cat stateの生成を確認することができました。
非古典状態のシミュレーションもお手軽にできるようです。計算機パワーは必要そうですが。
次はGKP符号を扱う予定です。
最後まで読んで頂きありがとうございました。
参考にした文献
- arXiv:quant-ph/0509137
- arXiv:quant-ph/0205044
- arXiv:quant-ph/0401001