Strawberry Fieldsで光量子計算をする(その5) ハミルトニアンの最小化

はじめに

今回紹介するアルゴリズムは、ボゾンからなる多体系のハミルトニアンの時間発展を計算することができます。

問題設定としては、
- 複数のノードからなるグラフ(格子)があり
- 各粒子は何れかのノードに存在することができる
- 粒子はボゾンの性質をもつ(各ノードに複数存在できる)

直接的には、ボーズ-アインシュタイン凝縮されたボゾンの振る舞いに対応するそうです。
応用可能性は後に紹介します。

理論

ハミルトニアン(Bose-Hubbard Hamiltonian)は以下の通りです。

$$
\begin{align}
H &= J \sum_i \sum_j A_{ij}\hat{a_i}^\dagger \hat{a_j} + \frac{1}{2}U \sum_i \hat{n_i} (\hat{n_i}-1)\
\end{align}
$$

J : hopping term (格子内でのボゾンの移動しやすさ)
U : on-site 相互作用ポテンシャル
A : 格子におけるボゾンの配置を表す隣接行列

on-site の意味はわからなかったので少し調べてみました。
元々、Bose-Hubbard Hamiltonian は固体物理や結晶物理における Hubbard model というものに由来するらしいです。後者はフェルミオンについてのモデルで、前者はそのボゾン版らしく。
Hubbard model では on-site Coulomb repulsion とは同一原子の軌道にいる電子間の力を指すようです。Bose-Hubbard Hamiltonian の場合は同一格子点にいるボゾン同士の相互作用力を指します。
互いに反発する場合は、$U>0$です。

このHamiltonianで、格子が簡単に2点 $(i,j \in$ {1,2} ) のみの場合の時間発展を考えます。
隣接行列は以下の通りです。

A = 
\begin{bmatrix}
0 & 1 \\
1 & 0 
\end{bmatrix}

系の時間発展演算子はハミルトニアンがわかっていれば以下のように与えることができました。

$$
e^{-iHt} = \exp [{-iJ(\hat{a_1}^\dagger \hat{a_2}+\hat{a_2}^\dagger \hat{a_1}) - \frac{iU}{2}(\hat{n_1}^2 - \hat{n_1}+\hat{n_2}^2 - \hat{n_2}) }\ t]
$$

ここで Lie-product formula
$$
e^{A+B} = \lim_{k\to \infty} (e^{\frac{A}{k}}e^{\frac{B}{k}})^k
$$

というものを用いて、時間発展を$k$回の離散ステップに分解します。

\begin{align}
e^{-iHt} &= (e^{-i\frac{Ht}{k}})^k \\
&= \big[\exp \{-i\frac{Jt}{k}(\hat{a_1}^\dagger \hat{a_2}+\hat{a_2}^\dagger \hat{a_1}) - \frac{Ut}{2k}(\hat{n_1}^2 - \hat{n_1}+\hat{n_2}^2 - \hat{n_2}) \}\big]^k \\
&= \big[\exp \{-i\frac{Jt}{k}(\hat{a_1}^\dagger \hat{a_2}+\hat{a_2}^\dagger \hat{a_1})\} \exp \big(-i\frac{Ut}{2k}\hat{n_1}^2\big)\exp \big(-i\frac{Ut}{2k}\hat{n_2}^2\big) \exp\big(i\frac{Ut}{2k}\hat{n_1}\big)\exp\big(i\frac{Ut}{2k}\hat{n_2}\big)\big]^k
\end{align}

実際は $k$ は有限なので、$O(t^2 / k)$ の誤差項がつきます。
時間発展を有限ステップのゲート操作で近似する発想はQAOAと近いですね。

これを連続量光量子ゲート操作で書き換えたのが以下です。

$$
e^{iHt}=[BS(\theta, \phi)\ (K_1(r)R_1(-r) \otimes K_2(r)R_2(-r) )]
$$

格子点1と格子点2それぞれに対応する状態に対してRotation Gate と Kerr Gate をそれぞれ作用させ、最後に互いをBeam Splitterに突っ込みます。

Kerr gate

折角なので Kerr gate の様子を簡単に見てみます。

import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import scale
from numpy import pi, sqrt
import matplotlib.pyplot as plt

eng, q = sf.Engine(2)
r=3
alpha=1+1j

with eng:
    Coherent(alpha)  | q[0]
    Coherent(alpha)  | q[1]
    Kgate(r)  | q[1]

state = eng.run('fock',cutoff_dim=50)

x = np.arange(-5, 5, 0.1)
p = np.arange(-5, 5, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
plt.subplot(1, 2, 1)
plt.contourf(X, P, W)

W1 = state.wigner(1, x, p)
plt.subplot(1, 2, 2)
plt.contourf(X, P, W1)

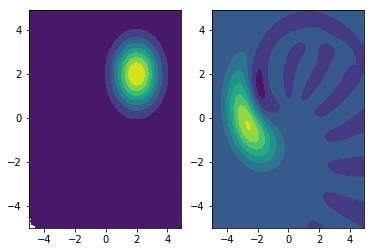
下記プロットが出力結果です。
コードでは確認用に同一のコヒーレント状態を2つ用意していて、左のプロットは入力そのまま、右のプロットは適当な Kerr gate を作用させたものです。

Kerr gate を作用させた右側は歪んでいますね。
この見た目が示すように、Kerr gate は ガウス操作ではなく、出力はガウス状態ではありません。
Kerr gate は光子数$\hat{n}^2$(光強度)に依存した位相変化を与えることに対応します。
プロットの位相平面では光子数は原点からの距離に対応し、原点から遠いほど位相回転が大きい形状になっていますね。

Hamiltonian Simulationの実装

では、Hamiltonian の時間発展を見てみましょう。
ここでは格子は2点でボゾン(光子)の総数が2としていますが、ボゾン数は適当に増やしても同様に計算可能だと思います。
(cutoff_dim はボゾン数より大きく設定する必要があります)

import strawberryfields as sf
from strawberryfields.ops import *
import matplotlib.pyplot as plt
%matplotlib inline

eng, q = sf.Engine(2)
J=1
U=1.5
k=20
t=1.086
theta = -J*t/k
r = -U*t/(2*k)
with eng:
    # prepare the initial state
    Fock(2) | q[0]


    for i in range(k):
        BSgate(theta, pi/2) | (q[0], q[1])
        Kgate(r)  | q[0]
        Rgate(-r) | q[0]
        Kgate(r)  | q[1]
        Rgate(-r) | q[1]

state = eng.run('fock', cutoff_dim=10)

print("[2,0] = ",state.fock_prob([2,0]))
print("[1,1] = ",state.fock_prob([1,1])) 
print("[0,2] = ",state.fock_prob([0,2]))

出力結果は以下になります。
例えば、この時間発展後にノード1にボゾンが2個いてノード1には0個である確率は約0.24ということになります。

[2,0] =  0.24194587742325968
[1,1] =  0.2356528768567246
[0,2] =  0.5224012457200199

1点だけ見ても系としてどんな挙動をしているのかよくわからないですね。
パラメータをいじって、かつ1ステップごとに確率を出力するように書き換えてみました。
(※パラメータは出力のプロットが滑らかになるよう設定しただけなので、現実のパラメータとは全くかけ離れている可能性があります)

import strawberryfields as sf
from strawberryfields.ops import *
import matplotlib.pyplot as plt
%matplotlib inline

J=1
U=1.5
k=40
t_step=0.1
iteNum = 100

A = []
B = []
C = []

for ii in range(iteNum):
    eng, q = sf.Engine(2)
    t = t_step * ii
    theta = -J*t/k
    r = -U*t/(2*k)
    with eng:
        # prepare the initial state
        Fock(2) | q[0]

        for i in range(k):
            BSgate(theta, pi/2) | (q[0], q[1])
            Kgate(r)  | q[0]
            Rgate(-r) | q[0]
            Kgate(r)  | q[1]
            Rgate(-r) | q[1]

    state = eng.run('fock', cutoff_dim=10)

    A.append(state.fock_prob([2,0]))
    B.append(state.fock_prob([1,1])) 
    C.append(state.fock_prob([0,2]))

plt.plot(A,label="[2,0]")
plt.plot(B,label="[1,1]")
plt.plot(C,label="[0,2]")
plt.legend()

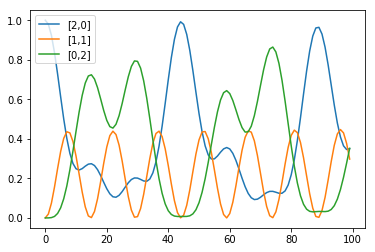
ノード1に2個のボゾンがある状態を初期状態として振動していますね。
2体の単純な系なので、妥当に思えます。
これが3体以上になっていくとより複雑な挙動を示しそうです。

アルゴリズムの詳細はこちらの資料でも解説されています。
こちらによるとBose-Hubbard Hamiltonian は superfluid と Mott insulator の状態遷移シミュレーションや、エンタングルメント生成の試験などに応用可能...だそうです。

まとめると、連続量光量子計算でもハミルトニアンの時間発展を近似的に解くスキームがあります。
ただし解きたい系において粒子がボゾンの性質を持っている必要がありそうです。
フェルミオン(電子)による量子計算系と相補的な関係となるのかもしれませんね。

以上、読んで頂きありがとうございました。

参考にした文献

・https://strawberryfields.readthedocs.io/en/latest/algorithms/hamiltonian_simulation.html
・https://en.wikipedia.org/wiki/Hubbard_model
・https://math.stackexchange.com/questions/2030671/proving-the-lie-product-formula
・https://arxiv.org/abs/1801.06565