以前 (https://qiita.com/ryuNagai/items/f8f20c9376c72103e878) に量子状態をMatrix Product States(MPS)として計算する手法の実装について記事を書きました。
この時は状態ベクトル→MPSの変換と簡単なゲート操作を扱いましたが、今回はMPSに対応する演算子MPO(Matrix Product Operator)とMPSを用いた期待値計算を実装したので簡単に紹介します。
前回に引き続き、全体の内容は http://arxiv.org/abs/1008.3477 (参考文献[1])を参考としています。
復習: MPSについて
MPSは、量子状態を行列同士の積で表すものでした。
MPSは下図[1]のように表現されます。
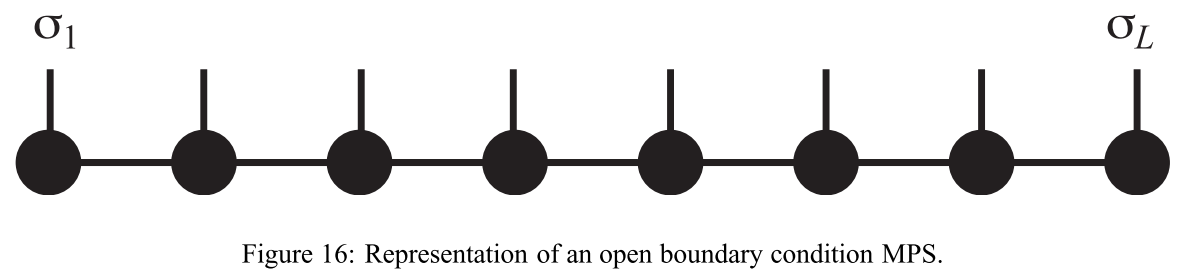
各黒丸は"site"と呼ばれ、N qubit系であればN個のsiteが作られます。
$\sigma_i$は"physical index"と呼ばれ、qubitの場合は$0\ (|0\rangle)$ or $1\ (|1\rangle)$を指します。各siteは通常の2次元行列にphysical indexの次元を加えた3次元行列(テンソル)と考えます。
各siteはそれぞれphysical index=0に対応する2次元行列と、physical index=1に対応する2次元行列を持つとイメージすることもできます。
仮に全ての$i$について$\sigma_i = 0$の場合、全てのsiteのphysical index=0に対応する2次元行列同士の積を計算することができ、その結果はもとの量子状態における$|00...0>$の係数となります。
同様に各siteのphysical indexを変えて対応する行列同士の積をとれば、元の状態ベクトルにおいて対応する計算基底状態の係数が得られます。
一旦physical indexは任意として、$i$番目のsite $(l,m)$と $j$番目のsite $(m,n)$の行列積 $(l,m)\times(m,n)$ では $m$個の要素について縮約が取られるわけですが、この $m$ の数がbonding dimensionと呼ばれます。
siteの数(=qubitの数)が多くともbonding dimensionが小さければ量子状態を表すために保有するパラメータも計算量も小さくて済みます。
ある精度で量子状態をMPS表現するために必要なbonding dimension の大きさは、量子状態が持つエンタングルメントに依存します。
一般に状態ベクトル表記はqubit数が増えると行列要素が指数関数的に増えますが、MPSにおいてはそうと限りません。あくまでエンタングルメントの大きさで(あるいは要求する精度の厳しさ)で必要な計算リソースが決まります。
MPOと期待値計算について
状態の行列積表現MPSに対する、演算子の行列積表現です。
$$
\hat{O^{[l]}} = \sum_{\sigma_{l},\sigma'_{l}} O^{\sigma_l,\sigma'_l}|\sigma_l\rangle\langle\sigma'_l|
$$
$\sigma, \sigma'$は先程のMPSと同様にphysical dimensionを指します。
MPSと合わせて図で表現すると以下のようになります[1]。

この図は$\langle\phi|\hat{O}|\psi\rangle$ を表していて、$|\phi\rangle=|\psi\rangle$であれば$\hat{O}$の状態ベクトルにおける期待値計算となります。
状態ベクトルはそれぞれMPSとして表されており、MPOはMPSの間に挟まれる形です。$\hat{O}$が無い場合は状態ベクトル同士の内積計算となります。
site同士を結ぶエッジでは、対応する次元の縮約計算が行われており、図中の全てのエッジにおいて縮約を行うと、最終的な出力はスカラーになります。
期待値計算は注目したいハミルトニアンについて行いたいケースが多いと思いますが、これをMPOとして表現するには一手間が必要です。
例えば簡単な3qubit系のハミルトニアン$H=Z_1 Z_2 + Z_2 Z_3$をMPOに落とし込むには、以下のように3つの行列に分解します。
$$
\left[\begin{array}{c}
Z_1 & I_1\
\end{array}\right]
\left[\begin{array}{c}
Z_2 & 0 \
0 & Z_2 \
\end{array}\right]
\left[\begin{array}{c}
I_3\
Z_3
\end{array}\right] \quad
$$
3つの行列はそれぞれ上図でsite $i$ に挟まれるMPOに対応します。
また行列積計算を行うと、元のハミルトニアンと同じ形になります。
行列の要素となっているpauli演算子はそれぞれ $2\times 2$ 行列のため、この場合 site $2$ のMPOはサイズ$2\times 2 \times 2 \times 2$ を持ちます。
実装
実装は自作モジュール"MPS.jl"にまとめました。
前回に引き続きJulia、versionは 1.4 で確認しています。
https://github.com/ryuNagai/MPS/blob/master/TN_Julia/MPS.jl
以下のように"MPS.jl"をincludeして、"using .MPSforQuantum"でimportできます。
include("./MPS.jl")
using .MPSforQuantum
MPOの作成
まずpauli演算子を用意し、自作module内関数"dstack", "ddstack"を使って各siteのpauli演算子行列を作り、リスト O に格納しています。
ここは出来ればもう少しスッキリ書けるようにしたいです...。
$$
\left[\begin{array}{c}
Z_1 & I_1\
\end{array}\right]
\left[\begin{array}{c}
Z_2 & 0 \
0 & Z_2 \
\end{array}\right]
\left[\begin{array}{c}
I_3\
Z_3
\end{array}\right] \quad
$$
pauliZ = convert(Array{ComplexF64,2}, [1 0; 0 -1])
pauliI = convert(Array{ComplexF64,2}, [1 0; 0 1])
zero = convert(Array{ComplexF64,2}, [0 0; 0 0])
O = []
push!(O, dstack((pauliZ, pauliI)))
push!(O, ddstack([(pauliZ, zero), (zero, pauliZ)]))
push!(O, dstack((pauliI, pauliZ)))
期待値計算
先程作ったMPOについて、3 qubitで張れる8つの計算基底状態 $|000\rangle$~$|111\rangle$ における期待値を計算します。
N = 3 # site数
D = 10 # Max bond dimension
eps = 1e-3 # SVD cutoff threshold
for i in 1:8
C0 = zeros(ComplexF64, 2^N)
C0[i] = 1 #各計算基底状態の状態ベクトルを用意
mps = MPS(C0, eps) # MPSを用意
expc = expectation(mps, O) # 期待値計算
println(expc)
end
実行結果
2.0 + 0.0im # |000>
0.0 + 0.0im
-2.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
-2.0 + 0.0im
0.0 + 0.0im
2.0 + 0.0im # |111>
通常の状態ベクトルによる計算を用いた確認
通常の状態ベクトルを用いた計算で、同様の結果が得られる事を確認します。
難しい事を考えずに使えるテンソル積関数が意外と見つからなかったので書きました。
function tensordot(x::Array, y::Array)
lx = size(x)
ly = size(y)
res = zeros(lx[1] * ly[1], lx[2] * ly[2])
for i in 1:lx[1]
for j in 1:lx[2]
res[ (1+(i-1)*ly[1]):(ly[1]+(i-1)*ly[1]), (1+(j-1)*ly[2]):(ly[2]+(j-1)*ly[2]) ] = x[i,j] * y
end
end
return res
end
# Hamiltonian
H = tensordot(tensordot(pauliZ, pauliZ), pauliI) + tensordot(tensordot(pauliI, pauliZ), pauliZ)
for i in 1:8
vec = zeros(ComplexF64, 8)
vec[i] = 1 #各計算基底状態の状態ベクトルを用意
expc = transpose(vec) * H * vec # 期待値計算
println(expc)
end
実行結果
2.0 + 0.0im
0.0 + 0.0im
-2.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
-2.0 + 0.0im
0.0 + 0.0im
2.0 + 0.0im
結果は同じです。問題なさそうですね。
まとめ
MPSとMPOによるハミルトニアンの期待値計算ができました。
次のマイルストーンとしては、ハミルトニアンにおける基底状態の探索を実装しています。
参考文献
[1]arXiv:1008.3477 (http://arxiv.org/abs/1008.3477)