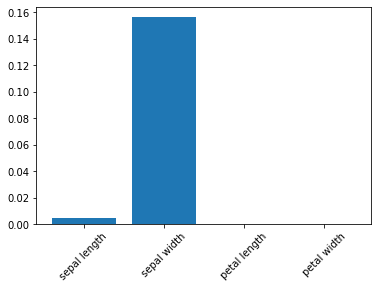【Python】 単変量統計による特徴量選択

はじめに

単変量統計とは、個々の特徴量とターゲットとの間に統計的に顕著な関係があるかどうかを計算し、最も高い確信度で関連している特徴量を選択しようとする手法です。

この手法は単変量であるため、他の特徴量と組み合わさって意味を持つような特徴量は捨てられてしまいます。
利点としてはモデルを構築する必要がなく、計算が高速な点です。
欠点としてはモデルベース特徴量選択や反復特徴量選択に比べ精度が劣る点です。

プログラム（カイ二乗統計を用いた場合）

chi2.py

# 単変量統計
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest

# それぞれの特徴量と目的変数間のカイ二乗統計量を計算
from sklearn.feature_selection import chi2

columns = ['sepal length','sepal width','petal length','petal width']
iris = load_iris()
X, y = iris.data, iris.target

# 特徴量を2つに絞る
selector = SelectKBest(chi2, k=2)
X_new = selector.fit_transform(X, y)

print('original features count: {}, selected features count: {}'.format(X.shape[1], X_new.shape[1]))
print('feature importance: ', selector.scores_)
print('pvalues: ', selector.pvalues_)

実行結果

original features count: 4, selected features count: 2
feature importance: [ 10.81782088 3.7107283 116.31261309 67.0483602 ]
pvalues: [4.47651499e-03 1.56395980e-01 5.53397228e-26 2.75824965e-15]

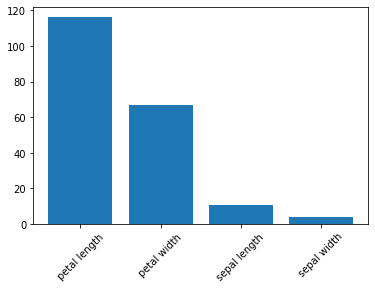
カイ二乗スコアをグラフ表示

chi2_plot.py

import matplotlib.pyplot as plt

# 特徴量とカイ二乗スコアを結合
feature_scores = list(zip(selector.scores_,columns))
# 降順にソート
sorted_feature_scores = sorted(feature_scores,reverse=True)

# 特徴量とカイ二乗スコアを分割
num_list = []
col_list = []
for i in range(4):
   num_list.append((sorted_feature_scores[i])[0])
   col_list.append((sorted_feature_scores [i])[1])


plt.bar(col_list,num_list)
plt.xticks(rotation=90)
plt.savefig('feture_score.png')

実行結果

p値をグラフ表示

chi2_p_value_plot.py

plt.bar(columns,selector.pvalues_)
plt.xticks(rotation=45)
plt.savefig('feture_pvalues.png')

実行結果

考察

カイ二乗スコアは「petal length」、「petal width」が4つの特徴量の内で比較的高い値を示している。しかし、p値は「sepal length」、「petal length」、「petal width」の3つが00.5以下なのでこの3つがカイ二乗スコアとして高い値を示していると言える。

よって、2つ選ぶとすれば「petal length」、「petal width」となるが、「sepal length」、「petal length」、「petal width」の3つを選ぶのが妥当と言える。