この記事(動画)がちょっとした話題になっていたので、数学的な証明は置いておいて、数値的にどうなっているのかnumpyで計算してみる。
この記事のnotebookはこちら
検証環境
- Python: 3.6.5 (Anaconda)
- numpy: 1.14.3
- matplotlib: 2.2.2
円弧の計算と描画
円弧の式は
$x^2 +y^2 = 4$
$\Rightarrow$ $y = \pm\sqrt{4-x^2}$
右上の扇形なので $y = \sqrt{4-x^2}$
numpyで計算してみる
import numpy as np
def get_arc(n): # 後々のために関数化
x = np.linspace(0, 2, n)
y = np.sqrt(4 - x**2)
return x, y
n_pi = 1000 # 円弧を描くときの点数
x_pi, y_pi = get_arc(n_pi)
プロットする
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
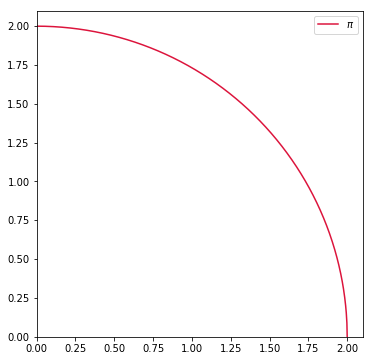
plt.plot(x_pi, y_pi, label="$\pi$", c="#dc143c")
plt.axis("scaled")
plt.xlim(0,2.1)
plt.ylim(0, 2.1)
plt.legend()
階段状の線分の計算と描画
円弧上の点を階段状につなぐ線分を計算する。点は等間隔になっている必要はないが、面倒なのでxを等間隔に区切る。
この線分は$(x_1,y_1), (x_2, y_1), (x_2,y_2),...,$ とx,yが交互に増えていくのでnp.repeatを使って下記のようにかける。
(np.r_[]はnp.ndarrayをaxis=0の方向に結合する)
def get_step(n):
x_step = np.linspace(0, 2, n)
y_step = np.sqrt(4 - x_step**2)
x_step = np.r_[x_step[0], np.repeat(x_step[1:], 2)]
y_step = np.r_[np.repeat(y_step[:-1], 2), y_step[[-1]]]
return x_step, y_step
描画する
n_step = 5 # 円弧上の点数
plt.figure(figsize=(6,6))
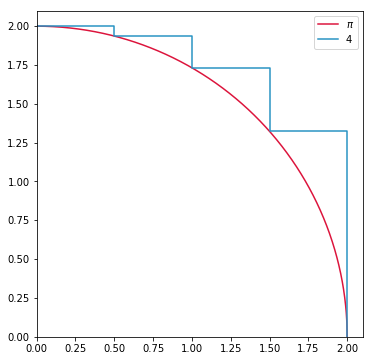
plt.plot(x_pi, y_pi, label="$\pi$", c="#dc143c")
plt.plot(*get_step(n_step),label="4", c='#2792c3')
plt.axis("scaled")
plt.xlim(0,2.1)
plt.ylim(0, 2.1)
plt.legend()
点の数を増やしてみる
plt.figure(figsize=(6,6))
fig = plt.gcf()
for n_step in [5,10,100,1000]:
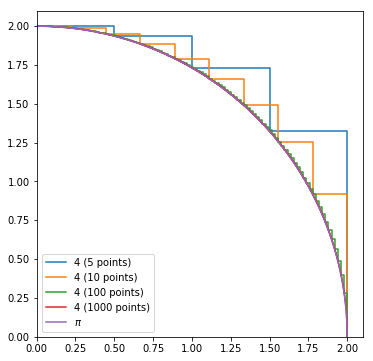
plt.plot(*get_step(n_step), label=f"4 ({n_step} points)")
plt.plot(x_pi, y_pi, label="$\pi$")
plt.axis("scaled")
plt.xlim(0,2.1)
plt.ylim(0, 2.1)
plt.legend()
1000点までいくと、円弧のグラフとほとんど重なっているように見える
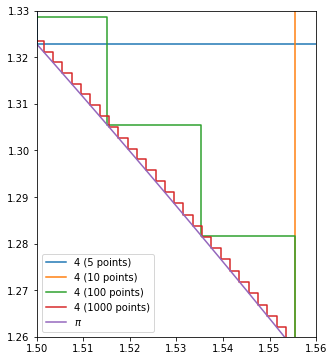
拡大してみる
ax=fig.axes[0]
ax.set_xlim(1.5,1.56)
ax.set_ylim(1.26, 1.33)
fig
長さの計算
隣り合う点同士を結んだ線分の長さの合計値を計算してみる
(長さ) $=\sum_{i=2}^N \sqrt{(x_{i-1} - x_i)^2 + (y_{i-1} - y_i)^2}$
円弧の長さ
点数を変えて$\pi$に近づくことを検証する
def calc_distance(points):
return np.sum(np.sqrt(np.sum((points[:-1]-points[1:])**2,1)))
for n_pi in [10,100,1000,10000]:
points_pi = np.c_[get_arc(n_pi)]
print(f"arc ({n_pi:5d} points): {calc_distance(points_pi)}")
arc ( 10 points): 3.130663103415464
arc ( 100 points): 3.1412940991313274
arc ( 1000 points): 3.1415833423863937
arc (10000 points): 3.1415923595492683
ちなみに
np.pi
3.141592653589793
なので10000点あれば小数点以下5桁くらいはあっている
階段線分の長さ
同じく点の数を変えて計算する
for n_step in [10,100,1000,10000]:
points_step =np.c_[get_step(n_step)]
print(f"step ({n_step:5d} points): {calc_distance(points_step)}")
step ( 10 points): 4.0
step ( 100 points): 4.0
step ( 1000 points): 4.0
step (10000 points): 4.0
点の数を変えても常に4であることがわかる
おまけ
解析的に円弧の長さを計算する(11/14 めちゃくちゃ間違えていたので修正)
https://mathtrain.jp/kotyoによると、$y=f(x)$ であらわされる曲線の長さはfが連続微分可能なら
$\int_a^b\sqrt{1+f'(x)^2}dx$
であらわされるらしい
x = sympy.var("x")
y = sympy.sqrt(4-x**2)
dy_dx = sympy.diff(y, x)
sympy.integrate(sympy.sqrt(1+dy_dx**2), (x, 0, 2))
pi