とりあえず、pythonでLASSO回帰分析を行いたい人向けです。パラメータはいじりません。
使用するデータはこちらhttps://gist.github.com/tijptjik/9408623
*一番下に、全てをまとめたコードがあります。
LASSO回帰用のモジュールをインポート
sklearn.linear_modelの中から、Lassoだけをインポートします。
from sklearn.linear_model import Lasso
データを分割するモジュールをインポート
sklearn.model_selectionの中から、train_test_splitだけをインポートします。
from sklearn.model_selection import train_test_split
行列を扱うモジュールをインポート
numpyをnpという名前で使用できる状態でインポートします。
import numpy as np
csvを扱うモジュールをインポート
pandasをpdという名前で使用できる状態でインポートします。
import pandas as pd
グラフを描くモジュールをインポート
import matplotlib.pyplot as plt
平均平方二乗誤差を求めるモジュールをインポート
from sklearn.metrics import mean_squared_error
csvを読み込む
df(データフレーム)に、iris.csvを読み込む。
df=pd.read_csv('wine_type.csv')
*('iris.csv')はカレントディレクトリからcsvファイルへのアクセスです。
pythonをデスクトップで実行し、Desktop>Documentsにcsvがある場合は、
df=pd.read_csv('Desktop/Documents/wine.csv')
などとなります。(Linux)
データを訓練用、テスト用に分ける
訓練:学習=6:4にします。
df_train, df_test = train_test_split(df, test_size=0.4)
データを表示するとこんな感じです。
df_train=
wine_type alcohol malic_acid ash alcalinity_of_ash magnesium total_phenols flavanoids nonflavanoid_phenols proanthocyanins color_intensity hue OD280/OD315_of_diluted_wines proline
106 2 12.25 1.73 2.12 19.0 80 1.65 2.03 0.37 1.63 3.40 1.00 3.17 510
157 3 12.45 3.03 2.64 27.0 97 1.90 0.58 0.63 1.14 7.50 0.67 1.73 880
75 2 11.66 1.88 1.92 16.0 97 1.61 1.57 0.34 1.15 3.80 1.23 2.14 428
142 3 13.52 3.17 2.72 23.5 97 1.55 0.52 0.50 0.55 4.35 0.89 2.06 520
83 2 13.05 3.86 2.32 22.5 85 1.65 1.59 0.61 1.62 4.80 0.84 2.01 515
.. ... ... ... ... ... ... ... ... ... ... ... ... ... ...
117 2 12.42 1.61 2.19 22.5 108 2.00 2.09 0.34 1.61 2.06 1.06 2.96 345
129 2 12.04 4.30 2.38 22.0 80 2.10 1.75 0.42 1.35 2.60 0.79 2.57 580
60 2 12.33 1.10 2.28 16.0 101 2.05 1.09 0.63 0.41 3.27 1.25 1.67 680
25 1 13.05 2.05 3.22 25.0 124 2.63 2.68 0.47 1.92 3.58 1.13 3.20 830
41 1 13.41 3.84 2.12 18.8 90 2.45 2.68 0.27 1.48 4.28 0.91 3.00 1035
[106 rows x 14 columns]
説明変数と目的変数を分ける
xには分析に使いたい列を挿入します。(説明変数)
yには分析の結果の列を挿入します。(目的変数)
今回は、'color_intensity'から'proline'を予測します。
x_train = df_train[['color_intensity']]
x_test = df_test[['color_intensity']]
y_train = df_train['proline']
y_test = df_test['proline']
空モデルを作る
lss = Lasso()
回帰の学習を行う
fit(説明変数、目的変数)
で学習を行い、上で作ったモデルlssに学習した結果が保持されます。
lss.fit(x_train, y_train)
回帰を行う
predict(回帰分析を行うデータ)
で回帰を行い、y_predに代入します。
y_pred = lss.predict(x_test)
グラフに表示してみる
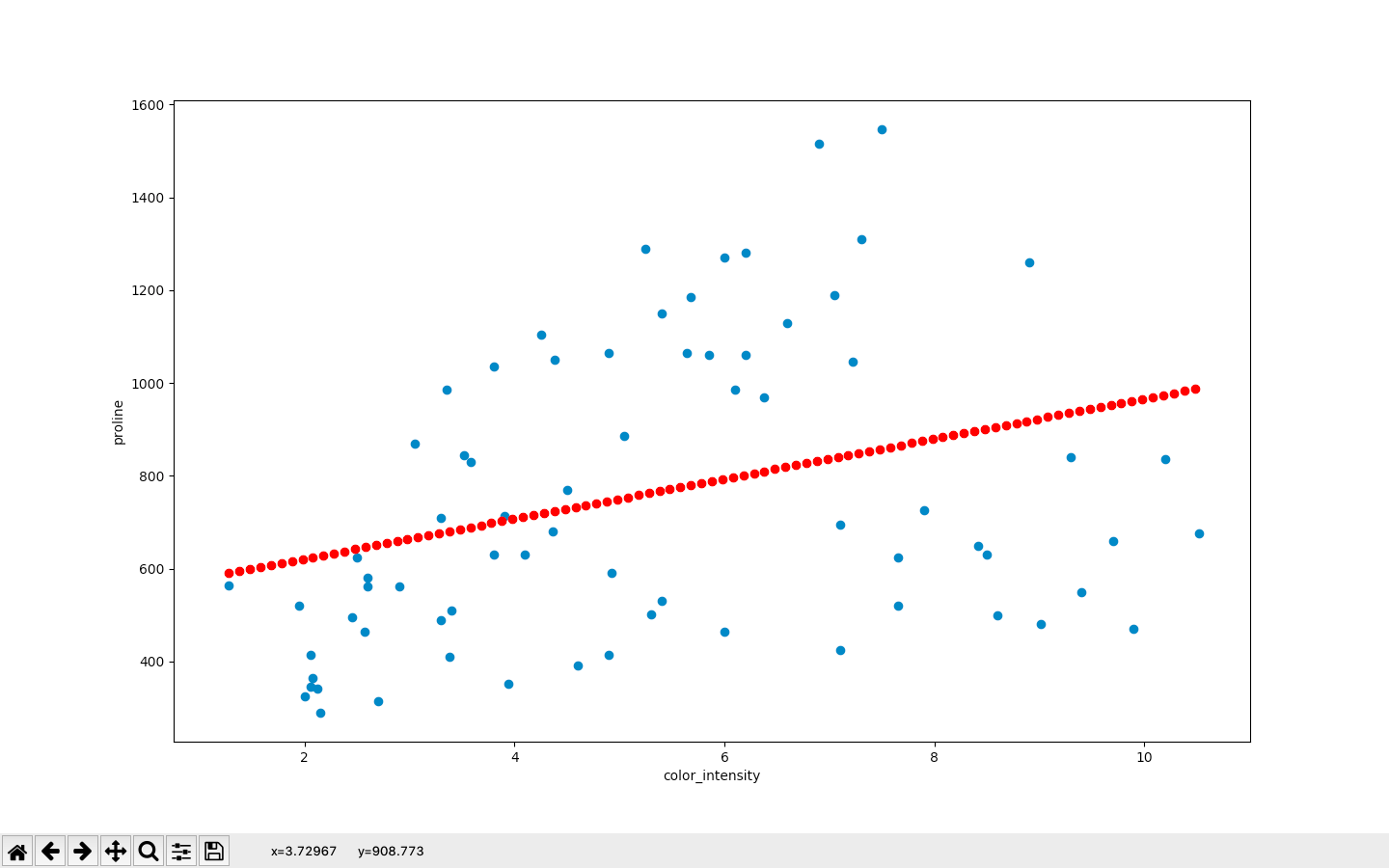
plt.scatter(x軸、y軸)で散布図を作ることができます。
正答を表示します。(青い点)
plt.scatter(x_test, y_test)
x_test["color_intensity"]の最小値から、最大値まで0.1刻みの配列を作り、行列にします。
そしてlss.predictにかけ、予測値を表示します。(赤い点)
x_for_plot = np.arange(np.min(x_test["color_intensity"])
,np.max(x_test["color_intensity"]),0.1).reshape(-1,1)
plt.scatter(x_for_plot,lss.predict(x_for_plot),color="red")
ラベルの設定
plt.xlabel("color_intensity")
plt.ylabel("proline")
表示
plt.show()
最後に、平均平方二乗誤差を求めます。
print(mean_squared_error(y_test,y_pred)) #90027.41397601982ですって笑
パラメータをいじるともっと精度が上がると思います。
以下コピペ用コード
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
df=pd.read_csv('wine.csv')
df_train, df_test = train_test_split(df, test_size=0.4)
x_train = df_train[['color_intensity']]
x_test = df_test[['color_intensity']]
y_train = df_train['proline']
y_test = df_test ['proline']
print(y_train)
lss = Lasso()
lss.fit(x_train, y_train)
y_pred = lss.predict(x_test)
plt.scatter(x_test, y_test)
x_for_plot = np.arange(np.min(x_test["color_intensity"]),np.max(x_test["color_intensity"]),0.1).reshape(-1,1)
plt.scatter(x_for_plot,lss.predict(x_for_plot),color="red")
plt.xlabel("color_intensity")
plt.ylabel("proline")
plt.show()
print(mean_squared_error(y_test,y_pred))