はじめに

　前回は因果分析のうち、因果推論について取り扱いました。因果推論は、説明変数が目的変数に与える影響度合いを推計するもので、これによって施策の効果を推計できるものです。
　本記事は、因果分析のうち、因果探索を扱います。因果探索は与えられたデータ間の因果関係を特定するものです。これによって今まで把握できなかった経営にとって有用な示唆を得ることができます。また、これまで常識としていた因果関係をもとに定義していたKPIが見せかけのものであることを把握することも可能です。
　私が参考にしている「Pythonによる因果分析」は、この因果探索の方法として、①LiNGAM、②ベイジアンネットワーク、③GANの応用、が紹介されています。そこで、今回は本書を参考に実装を進めるとともに実装上の論点となりうる事項をまとめたいと思います。

LiNGAM

LiNGAMは、因果関係を表す構造化方程式を行列式として表現し、この行列式を解くことによって因果行列を得ようというものです。LiNGAMについて理解するためにはこの行列式の構成要素である因果行列が何を表そうとしているのかを理解することが重要です。そうでないと、LiNGAMのポイントである『非循環』や『非ガウス』について手触り感のある理解をすることが難しくなります。このあたりについて「Pythonによる因果分析」（以下、本著という）はあまり説明にページを割いていないので、以下に自分なりの解釈を記載します。

　まず、以下のような仮想の問題設定をします。

１）観光エリアXは、観光スポットa1とa2とa3によって構成されている。
２）各観光スポットは互いに交通網で接続されており、旅行者が自由に行き来できる。
３）過去の調査から、以下がわかっている。
　　・ある時点（tとする）の観光スポットa1の旅行者は、t+1において0.5はその場にとどまり、0.15はa2に移動し、0.35はa3に移動する。
　　・同様に観光スポットa2の旅行者は、0.25がその場にとどまり、0.35はa1に移動し、0.4はa3に移動する。
　　・観光スポットa3の旅行者は、0.2がその場にとどまり、0.35がa1に移動し、0.45がa2に移動する。
４）今、t=nにおいて観光スポットa1,a2,a3に100,200,300の旅行者がいた場合、t=n+1における各観光スポットの旅行者数はどれだけになるのか？

　まず、起点となる観光スポットを横軸、終点となる観光スポットを縦軸として移動率を表にまとめます。

	起点a1	起点a2	起点a3
終点a1	0.50	0.35	0.35
終点a2	0.15	0.25	0.45
終点a3	0.35	0.40	0.20

この表をnumpyのarray（つまり行列）として設定すると、t=n+1における旅行客数は簡単に求めることができます。

coef = np.array([[0.50,0.35,0.35],[0.15,0.25,0.45],[0.35,0.40,0.20]])
passenger = np.array([[100],[200],[300]])

print(coef@passenger)

先の仮想例題においてt時点の各観光スポットの旅行者数を原因としてt+1時点の旅行者数を結果とみなすと、coefは因果行列にあたります。LiNGAMは、原因にあたるデータと結果にあたるデータが存在している状況下で不明である因果行列を推計しようというものだということになります。（実際には、説明変数=目的変数として因果行列を推計するので、この説明は正しくありません）
　因果行列のイメージがついたところで、LiNGAMの前提とする非循環を行列で表現します。非循環とは、先の仮想問題でいうと、観光スポットの添え字が小さいものから大きいものへの移動が許容されているが、同じまたは小さいものへの移動が許容されていない状況を指します。これは、因果行列の該当する要素にゼロを設定することで表現します。
続いて非ガウスです。先の仮想例題には外生変数が考慮されていません。具体的にいうと観光エリアx以外からの流入が考慮されていません。この外生変数の考慮は容易で、先に計算結果に外生変数のベクトルを加算すればいいことになります。

coef = np.array([[0.50,0.35,0.35],[0.15,0.25,0.45],[0.35,0.40,0.20]])
passenger = np.array([[100],[200],[300]])
ex = np.array([[5],[7],[9]])

print(coef@passenger + ex)

上記は、tからt+1推移すると、a1に5、a2に7、a3に9が流入するとした推計式を表しています。ここでは簡単になるように外生変数を固定にしていますが、通常は何らかの確率分布よりランダムに作成されたものと考えます。この確率分布をガウス分布以外を前提としようというものがLiNGAMということになります。

LiNGAMの実装

　いよいよ実装します。本著ではスクラッチで実装していますが、ここではLiNGAMの第一人者である清水昌平先生の公開するモジュールを使用します。
（URL：https://sites.google.com/view/sshimizu06/lingam)

　実験用データは以下の関数を使って生成します。

def data_create(num_data,SEED) :


# 非ガウスの外生変数
    ex1 = stats.expon.rvs(loc=0,scale=0.5,random_state=SEED,size=num_data)
    ex2 = stats.expon.rvs(loc=0,scale=1.5,random_state=SEED+1,size=num_data)
    ex3 = stats.expon.rvs(loc=0,scale=0.5,random_state=SEED+2,size=num_data)
    ex4 = stats.expon.rvs(loc=0,scale=1.5,random_state=SEED+3,size=num_data)

# データ生成

    x1 = ex1
    x2 = 0.3*x1 + ex2
    x3 = 2.5*x1 + 4*x2 + ex3
    x4 = 5*x2 - 2*x3 + ex4

# 表にまとめる
    df = pd.DataFrame({"x1": x1, "x2": x2, "x3": x3, "x4":x4})
    ex = pd.DataFrame({"ex1":ex1,"ex2":ex2,"ex3":ex3,'ex4':ex4})
    return df,ex

ポイントは、x4の生成過程です。見かけ上、x1はx2を介してx4に影響していますが、直接影響していないものとしています。このあたりはどのような結果となって出力されるのかを確認します。
　実装はsklearnの関数と似ていて簡単です。

num_data= 20000
seed = 1234

df,ex = data_create(num_data,seed)   #### データの生成

from lingam import ICALiNGAM

causal_model = ICALiNGAM()
result = causal_model.fit(df.values)  #### Modelの適用

causal_matrix = result.adjacency_matrix_   #### 因果行列の出力

結果は以下となり、データ作成時のパラメータと近似した結果が得られました。

	x1	x2	x3
x1	0.0	0.0	0.0
x2	0.289	0.0	0.0
x3	2.510	3.999	0.0
x4	-0.039	4.938	-1.986

ただし、(x4.x1)の結果が-0.039と微妙がものとなりました。このパラメータはゼロが正しいのですが、観測値の関係でゼロを推計できませんでした。そこで、改めてx4を推計するモデルを構築して係数の検定を行うことにします。係数の検定にはstatsmodels.apiのOLSを用いると計算が便利です。

import statsmodels.api as sm

Y = df[['x4']]
x = df[['x1','x2','x3']]  ### LiNGAMの結果より特定された説明変数
X = sm.add_constant(x)    ### 切片部分があるモデルとして実装

ols_model = sm.OLS(Y,X)   ### 学習
result = ols_model.fit()

Pval = result.pvalues

結果としてx1の係数のP値は十分に大きく帰無仮説（係数=ゼロ）を棄却できませんでした。このように得られた因果行列に対して不信感を感じた場合は、あらためて回帰モデルを学習させて係数の評価を行うといいでしょう。

ベイジアンネットワーク

　ベイジアンネットワークは変数間の関係性をグラフ図（ネットワーク図）として表現するモデリング手法とベイズの定理を融合した因果関係を特定する手法です。
　最初に疑似データの生成を行います。

def data_create(Num_data,Seed) :

    x1 = stats.bernoulli.rvs(p=0.4,size=Num_data,random_state=Seed)
    x2 = stats.bernoulli.rvs(p=0.6,size=Num_data,random_state=Seed+1)

    coef1 = stats.norm.rvs(loc=0.5,scale=0.1,size=Num_data,random_state=Seed+2)
    coef2 = stats.norm.rvs(loc=0.25,scale=0.08,size=Num_data,random_state=Seed+3)

    x3 = x1*coef1 + x2*coef2 + stats.uniform.rvs(loc=-1,scale=1,size=Num_data,random_state=Seed+4)

    x4 = stats.uniform.rvs(loc=0,scale=1,size=Num_data,random_state=Seed+5)
    tmp = np.array([x3,x4])
    x5_prob = expit(np.array([[0.8,0.5]])@tmp)
    x5 = stats.bernoulli.rvs(p=x5_prob,random_state=Seed+5)

    df = pd.DataFrame([])
    df['x1'] = x1
    df['x2'] = x2
    df['x3'] = x3
    df['x4'] = x4
    df['x5'] = x5

    return df

data = data_create(2500,1234)

この変数x1～x5の初期状態の因果関係をグラフ図として表現すると以下のようになります。

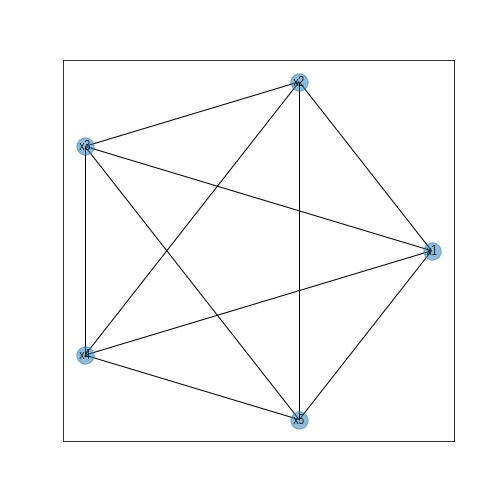
各ノードが変数であり、エッジは各変数間の因果関係の有無を表します。また、このエッジが矢印となっていればその向きに応じて因果関係が存在することとし、向きが存在しない場合は因果の向きが決まっていないこととします。つまり、ベイジアンネットワークの初期状態は、すべての変数間に因果関係がある、ただし、向きは未確定である、という状態と定義します。ベイジアンネットワークはこの初期状態から、①因果関係を認められないエッジを削除、②残ったエッジに対して向きを決定、という流れで最終的な因果関係を示すグラフ図を決定します。
　この因果関係が認められないことの評価ですが、独立性の検定を使用します。先の疑似データのx1とx2を例に考えます。この2変数のクロス集計は以下のようになります。

	x2=0	x2=1	合計
x1=0	621	877	1498
x1=1	385	617	1002
合計	1006	1494	2500

独立であるということは、x1=0の場合のx2の比率（つまり1が出現する確率）x1=1の場合のx2の比率が全体の比率と同じのことをいいます。今回、データ生成上、x1とx2のclass=1の確率は0.4と0.6なので、x1とx2が独立であれば、array([[0.24,0.36],[0.16,0.24]])の比率でデータは分布するはずです。この理論上の分布（期待度数）と実際に観察された度数の差異を統計値に換算して」p値を求めることで観測値の独立性を評価しようというものが独立性の検定（カイ二乗検定）になります。
　検定は、pgmpyというモジュールを使用します。本著で使用しているバージョンは0.9.0ですが、公開されている最新バージョンは0.15.0です。本記事は0.15.0を使用します。バージョン変更によりAPIが変更になっているのでコードを参考にする場合はバージョンに注意してください。

#### ベイジアンネットワークを適用するために離散値に変換
data_bin = data.copy()
data_bin['x3'] = np.int64(pd.cut(data_bin['x3'],bins=2,labels=np.arange(2)))
data_bin['x4'] = np.int64(pd.cut(data_bin['x4'],bins=2,labels=np.arange(2)))

#### 全変数の組み合わせを設定
import itertools
node_list = data_bin.columns.values
comb = itertools.combinations(node_list,2)

result = {}

for i in comb :
    chi,pvalue,degree_freedom = Est.CITests.chi_square(X=i[0],Y=i[1],Z=[],data=data_bin,boolean=False)

    result[i[0]+'_'+i[1]] = [pvalue]

　カイ二乗検定は離散値に適用するものなので、連続値であるx3とx4を離散値に置きかえます。binを細かくするほうが、元の分布に近似するので正確な評価が可能となります。ただし、カイ二乗検定の帰無仮説である期待度数を算出するためには縦計または横計がすべてのクラスにおいて非ゼロである必要があります。binsを細かくするとこの非ゼロの前提を満たさないことが起こるので考慮しながら離散化を行うようにしましょう。
　独立性の検定の対象は、変数間の全エッジになります。そこで、itertoolsの関数を用いて組み合わせを形成して順番にカイ二乗検定を行います。関数の引数は、XとYがクロス集計表の軸にあたるものです。Zはこのクロス集計表作成時の条件を付与する変数です。Zの使い方については後述することとし、ここでは引数を渡す必要がないことを表す空のリストを設定します。booleanオプションは検定結果のみを戻り値とする場合にTrueを指定します。今回はp値を見たかったのでFalseとしました。結果は以下のようになりました。

検定対象	p値
x1 , x2	1.406283e-01
x1 , x3	8.895711e-161
x1 , x4	2.637819e-01
x1 , x5	5.720664e-28
x2 , x3	1.006900e-34
x2 , x4	2.424676e-01
x2 , x5	2.284775e-05
x3 , x4	9.261846e-02
x3 , x5	1.806653e-76
x4 , x5	4.887805e-20

　閾値を何にしていたのかによりますが、0.025とすると(x1,x2)、(x1,x4)、(x2,x4)、(x3,x4)は独立とみなされました。この結果を踏まえて再びグラフ図を作成します。

　この段階では、複数のエッジを有するノードがあることからさらに独立性の検定を行います。上図のうち、(x1,x3,x5)に着目します。仮にx1->x3、x1->x5という因果関係が真実であった場合、x3とx5の間には見かけの従属関係が示されます。そこで、このx3とx5が見かけの従属関係であるかどうかを確かめるために、x1が取りうる値（今回の疑似データでいうと0または1）を条件付けしたときのカイ二乗検定を行います。直観的わかるようにX1,X3,x5をもとにクロス集計表を作成します。

		x5=0	x5=1
x1=0	x3=0	921	356
x1=0	x3=1	85	136
x1=1	x3=0	231	92
x1=1	x3=1	220	459

x1の条件付けしたカイ二乗検定は、上記のクロス集計表をx1=0の場合とx1=1の場合で分離して各々についてカイ二乗検定を行い、その結果を統合して評価します。これにより、x3とx5の非独立がx1の影響を受けたものなのかそうではないのかを評価できるようになります。実装は、先ほどの関数を用いることで実現できます。

tmp = pd.DataFrame(result).T  ### 0次の独立性にて削除されないエッジリストの作成
tmp = tmp[tmp[0].T<0.05]
edge_list = [(x.split('_')[0],x.split('_')[1]) for x in tmp.index.values]

import networkx as nx         ### 結果の可視化の兼ねてnetworkxによるオブジェクト生成
G = nx.Graph()
G.add_edges_from(edge_list)

adjacency = nx.to_pandas_adjacency(G)  ### 近接行列をpandasのDataFrameで出力

result1 = {}

for i in adjacency.index.values :     ### 近接行列のindexを評価対象に繰り返しカイ二乗検定を実施
    tmp = adjacency.loc[i,:]
    tmp = tmp[tmp==1].index.values    ### エッジが存在するノードを抽出
    if len(tmp)>=2 :                  ### エッジが２以上存在する場合に組み合わせを作成
        comb = itertools.permutations(tmp,2)

        for j in comb :
            _,pvalues,_ = Est.CITests.chi_square(i,j[0],[j[1]],data=data_bin,boolean=False)
            result1[i+'_'+j[0]+'_'+j[1]] = [pvalues]

　最初に0次の独立性検定によって保持されたエッジをnetworkxのグラフオブジェクトに変換して、そこから近接行列を作成します。近接行列の縦軸方向を評価対象（つまりchi_square()の引数X）とし、これとエッジが存在するノードの組み合わせ一覧を作成します。あとは、これらをchi_square()に設定すれば計算できます。引数Zは、先ほどのクロス集計表の第一軸（x1）に相当するものを設定します。つまり、Zに設定した変数によって条件づけられたXとYに設定した変数でクロス集計表を作成してカイ二乗検定を行うとイメージすればいいでしょう。
　結果、x1とx5、x2とx5は独立（他の変数の影響を受けた見かけの従属）と判定できました。この結果を踏まえ、0次の独立性によって生成されたグラフより(x1,x5)と(x2,x5)のエッジを削除してグラフ図を作成します。

G.remove_edges_from([('x1','x5'),('x2','x5')])

pos = nx.circular_layout(G)
nx.draw_networkx_nodes(G,pos=pos,alpha=0.5)
nx.draw_networkx_labels(G,pos=pos)
nx.draw_networkx_edges(G,pos=pos)
plt.show()

　この段階でまだ、三角形となるエッジが保持されているようであればさらに独立性の検定を実施しますが、今回の疑似データだと、ここからオリエンテーションルールに沿って向きを決定します。オリエンテーションルールがどのようなものかについて本著ではほとんど触れられていません。多少なりとも理解するには、「入門統計的因果推論（J Pearl,M Glymour,N Jewell著落海浩訳朝倉書店）」の２．グラフィカルモデルとその応用あたりを読み込むといいかと思います。この中に様々なグラフに対して従属・独立の条件が示されているので、この条件を満たす場合に記載のグラフであるといえることが理解できます。
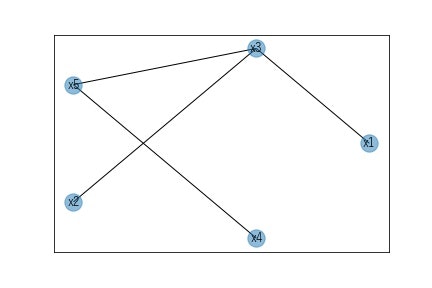
　例えば、(x3,x5,x4)に着目してオリエンテーションルールを適用すると、x5に対する合流点であることがわかるのでx3→x5とx4→x5という向きと決定します。同様に(x1,x2,x3)も合流点なので、x1→x3とx2→x3が因果関係の向きとして決定します。最後にx3とx5ですが、(x2,x3,x5)に着目すると0次の独立性の際は非独立で、x3を条件とすることで(x2,x5)は独立と判定されました。この条件を満たすのは連鎖のケースなのでx3→x5であると判定します。以上の結果をnetworkxを用いてグラフにすると以下になり、疑似データ作成時の因果関係をうまくとらえることができました。

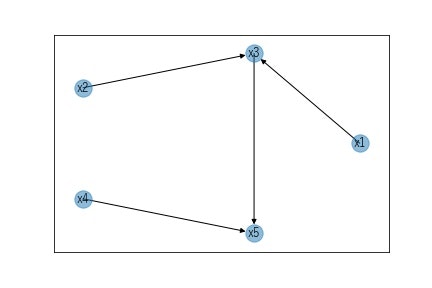
なお、pgmpyには上記の手続きをまとめて実行する関数が用意されています。よってこれを使うことで簡単に結果を得ることが可能です。

network = Est.PC(data_bin)
best_natwork = network.estimate()
edg_list = best_natwork.edges

G = nx.DiGraph()
G.add_edges_from(edg_list)
pos = nx.circular_layout(G)
nx.draw_networkx(G,pos=pos)

　結果として得られるグラフは形状の相違はあるものの、トポロジーとして同じなので手作業と同じ結果が得られました。実装も単純なので基本的にこちらを使用すればいいかと思います。

参考カイ二乗検定適用時の考慮事項

　ここで少し実験過程で把握した考慮事項を記載します。
　pgmpyのchi_squareですが、裏側でscipy.stats.chi2_contingencyを使用しています。このchi2_contingencyは、インプットとなるクロス集計表の縦計または横計にゼロが含まれていると計算不能となる制約があります。（実装を見ていませんが、期待度数の計算ができないことによるかと思います）chi_squareにはクロス集計表を作成する前のデータをインプットするため、この制約に引っかかっているかどうかがわかりません。特に1次の独立性以降になってくると引数Zに設定した変数の条件でデータを抽出した結果でクロス集計表を作成することになるため、この縦計または横計にゼロを含まないという条件を満たさないことが起こりえます。
pgmpyの実装（https://pgmpy.org/_modules/pgmpy/estimators/CITests.html 参照）によるとこの縦計または横計にゼロを含まないという条件を満たさないときは、try except構文を使ってうまく処理できるようにしています。しかしながら、条件によってはエラー時のワーニングメッセージを表示するコードで異常終了してしまいます。（本著の疑似データを用いて実装したところ、このエラーに遭遇し原因を理解するのに苦労しました）このワーニングメッセージ部分はカイ二乗検定の本質と無関係な部分なので、適宜、except以降のコードに手を加えるといいかと思います。（本質的には、カイ二乗検定が不可能な場合は評価対象から除く処理をしていると理解ください）
　それよりも以下に縦計または横計にゼロが含まれているケースの対策を以下に提案します。考え方として、クロス集計表上の値がゼロの要素が本当にゼロなのかを考えてみようというものです。仮にあるクラスの出現確率が極少（例えば0.0001）の場合、観測されるデータがゼロとなることはありますが、期待度数はゼロではありません。よって、ゼロとなったクラスに対して確率を推計してあげれば最終的に期待度数そのものも計算できるはずです。そこで、クロス集計表のある列が[0,10,20]の場合、この列が3クラスの多項分布に従うものと仮定してベイズ推計を行うことでクラス=0の確率を推計するといった方法を適用します。この処理を全ての列について実行すれば、カイ二乗検定可能なクロス集計表ができあがります。この計算結果は意味合いとして得られたデータから推測される尤もらしい度数ということになります。それゆえ実際の観測値とは異なるので正確性に問題はあるかもしれませんが、pgmpyの計算不能なケースはスキップして検定を行うよりはいいかもしれないと考えました。
　上記を実装したものを示します。

import pystan

#### Stanによるモデリング部分

stan_code= """
data {
    int COL ;
    int ROW ;
    int d[ROW,COL] ;
    int Summary[ROW] ;
}

parameters {
    simplex[COL] P[ROW] ;  // 多項分布の確率パラメータ
}

model {
    vector[COL] alpha;

    for (i in 1:COL) {
        alpha[i] = 1 ;
    }

    for (j in 1:ROW) {
        P[j][] ~ dirichlet(alpha) ;      // 事前分布としてディレクリ分布を使用
        d[j,] ~ multinomial(P[j][]) ;
    }
}

generated quantities {  // 推計したパラメータを用いたクロス集計表の推計
    int q[ROW,COL] ;
    for (i in 1:ROW) {
        q[i] = multinomial_rng(P[i],Summary[i]) ;
    }
}

"""
stan_model = pystan.StanModel(model_code=stan_code)

### テスト用データ
test_data = np.array([[10,20,0], [30,5,0]])

### Stan入力用データを作成
stan_data = {'ROW':test_data.shape[0],
             'COL':test_data.shape[1],
             'd':test_data,
             'Summary':test_data.sum(axis=1)}

result = stan_model.sampling(data=stan_data)    #### サンプリング

predict = result.extract()['q']                 #### 予測結果取得

stats.chi2_contingency(predict.mean(axis=0))

　ベイズ推計にはStanを使用しました。stan_codeとしてモデルを実装しています。入力値はクロス集計表です。この際の注意事項として縦計にゼロが含まれるクロス集計表をインプットさせることにしています。モデルにはgenerated quantities部に実際のクロス集計表の推計も加えました。
　テスト用のクロス集計表はtest_dataという変数です。先に触れたように縦計がゼロになるようにしています。モデルは、このデータを横軸方向にカットして多項分布のパラメータを学習して観測値がゼロの部分に対して非ゼロとなる結果を推計できるようにしています。推計結果はpredictとして抽出しています。この結果はサンプリング結果のため、１つの要素につき4000回（デフォルトを使用しているため。サンプリング時に指定可能）のサンプリング結果が得られているため、平均値を算出することで最終的なクロス集計表の推計結果が得られるようにしています。
上記を活用して疑似データを使って条件付きカイ二乗検定を試してみます。設定は、3変数によるクロス集計表が以下のようであったとします。

		x3=0	x3=1	x3=2
x1=0	x2=0	10	20	0
x1=0	x2=1	30	5	0
x1=1	x2=0	10	20	5
x1=1	x2=1	20	10	3
x1=2	x2=0	20	10	5
x1=2	x2=1	30	15	5

pgmpyのカイ二乗検定によると、x1の値で抽出したクロス集計表から個別に統計量を算出してその結果をまとめたものを使ってp値を算出しています。上記の場合であるとx1=0の場合、縦計にゼロを含むクロス集計表が存在するため、このケースをスキップしてp値を算出することになります。一方、先のクロス集計表のゼロとなっている要素を補完させれば、x1=０のケースも含めたp値を算出することができます。pgmpyの実装を参考にp値を算出したものを以下に示します。

	自由度	p値
x1=0をスキップ	4	0.00660
x1=0を補正	6	0.00159

結果としてx1=0のケースをクロス集計表を補正して計算に追加したほうがp値が小さくなりました。x1=0のx1とx3の関係を眺めてみると、従属性があるように見えるのでこの結果は妥当ではないかと考えます。

まとめ（仮）

　結構なボリュームになったので、いったんここで終わりにします。ベイジアンネットワークの構築方法には先のカイ二乗検定＋オリエンテーションルールでネットワークを特定するPCアルゴリズム以外にネットワークそのものの当てはまり具合を評価指標としたスコアリングによる構造学習などが存在します。次回は構造学習について触れたいと思います。また、ベイジアンネットワークの特徴的な推論についても触れたいと思います。推論とはネットワークが扱う変数のうち、一部だけがわかっている状況下で未知の変数について推論しようというものです。このあたりの理解が進むとこのベイジアンネットワークが生成モデルのような特性を持つことが垣間見え、本著が紹介するディープラーニング（GAN）を用いる手法が実現しようとしていることが見えてきます。

因果分析 初歩の初歩 その２