QuTiPがあまりに便利だったので,簡単な使い方をまとめておく。
この記事のほとんどは元記事QuTiP example: Vacuum Rabi oscillations in the Jaynes-Cummings modelの和訳である。
今までこういう記事を書いたことがなく,備忘録的に作ったものなので,著作権的にどうなのよ,みたいなことがあれば,記事自体を消去,もしくは別のモデルで改めて計算を行うつもりなので,遠慮なく言って欲しい。
また,今回記事を投稿した動機は,QuTiPを利用することでハミルトニアンの定義や量子マスター方程式を計算する手間を減らして解いてくれ,研究してる人や趣味で量子光学に取り組む人が,もっと本質的な物理を問題を考えることに集中するのを期待してだ。
モデルとしたJyanes-Cummings modelでRabi振動をデモンストレーションすることは対象として分かりやすいので,これを選んだ。
もちろんできることはここで書いたことだけでないので,物理系の方で少しでも興味を持っていただけるきっかけになれば嬉しく思う。
環境
QuTiP 4.2.0
Python 3.6.1
インストールは
pip install qutip
で出来たので,あまり苦労することもなかった。インストールに関する記事もあった。
今回は系の時間発展の計算を行ってみる。モデルとしては公式のチュートリアルの一番上にあった共振器量子電磁気学系(Jaynues-Cummings model)でRabi振動の計算を行うことにした。
図の描写と計算を行うためのライブラリをimportする。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from qutip import *
次にモデルの数値を代入していく。
wc = 1.0 * 2 * np.pi # 共振器の周波数
wa = 1.0 * 2 * np.pi # 2準位系の周波数
g = 0.05 * 2 * np.pi # 共振器と2準位系の結合定数
kappa = 0.005 # 共振器の緩和レート
gamma = 0.05 # 2準位系の緩和レート
N = 20 # 共振器の数状態の数
n_th_a = 0.0 # 2準位系の熱浴のレート
QuTiPは状態ベクトルを簡単に定義してくれる。例えば2準位系の基底状態のケットベクトルを定義しようと思うと,
TLSket=basis(2,0)
で定義できる。このときのアウトプットは
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
と出力される。ちょっと見にくけど,上が基底状態であるらしい。(正確には,この定義はフォトンのFock状態を1個までとることに対応している)
さて,共振器フォトンと2準位系のヒルベルト空間を考えて,ケットベクトルの直積を取る。ここで初期状態を与える。
psi0=tensor(basis(N,0),basis(2,1))
tensorが直積に当たるようだ。フォトンのFock状態を多く取ったので,出力は省略する。次に,共振器フォトンと2準位系の演算子を定義する。destroy(M)がFock状態をM個定義したベクトルの消滅演算子である。
例
destroy(5)
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = False
Qobj data =
[[ 0. 1. 0. 0. 0. ]
[ 0. 0. 1.41421356 0. 0. ]
[ 0. 0. 0. 1.73205081 0. ]
[ 0. 0. 0. 0. 2. ]
[ 0. 0. 0. 0. 0. ]]
Fock状態の消滅演算子を行列形式で書き下したときと同じ結果になっていることがわかる。
これを踏まえて,共振器フォトンと2準位系の消滅演算子を定義する。
a = tensor(destroy(N), qeye(2)) #共振器フォトンの消滅演算子
sm = tensor(qeye(N), destroy(2)) #2準位系の消滅演算子
共振器フォトンと2準位系の直積を取ることで,今回計算するヒルベルト空間上にそれぞれの消滅演算子を定義した。先に定義した初期状態と順番をあわせる必要がある。ここまで定義できると生成演算子は簡単で,
a.dag() #共振器フォトンの生成演算子
sm.dag() #2準位系の生成演算子
となる。先程定義した消滅演算子に.deg()と付けるだけでよい。
よくあるJaynes-Cummings modelのハミルトニアンは
\mathcal{H}=\hbar\omega_c a^\dagger a +\hbar\omega_a \sigma^\dagger \sigma+\hbar g (a^\dagger \sigma+a\sigma^\dagger)
であるので,上の定義を使って,
H = wc * a.dag() * a + wa * sm.dag() * sm + g * (a.dag() * sm + a * sm.dag())
と書ける。
QuTiPには量子マスター方程式のsolverがデフォルトで入っているので,上で定義した緩和レートを次のように定義する。
c_ops = []
# cavity relaxation
rate = kappa * (1 + n_th_a)
if rate > 0.0:
c_ops.append(np.sqrt(rate) * a)
# cavity excitation, if temperature > 0
rate = kappa * n_th_a
if rate > 0.0:
c_ops.append(np.sqrt(rate) * a.dag())
# qubit relaxation
rate = gamma
if rate > 0.0:
c_ops.append(np.sqrt(rate) * sm)
c_opsというところに,ルートを取った緩和レート×消滅演算子の配列を入れる。
あとは,ときたい時間の範囲を0から設定
tlist = np.linspace(0,15,301)
して,solverに入れるだけ,ここではそれぞれの励起状態の占有率
\langle a^\dagger a\rangle(t)\\
\langle \sigma^\dagger \sigma \rangle(t)
を計算してみる。solverには次のように書けば良い。
output = mesolve(H, psi0, tlist, c_ops, [a.dag()*a, sm.dag()*sm])
ハミルトニアン,初期状態,時間範囲,緩和レートを与えた後に,かぎかっこ内部にときたい演算子を入れてやると答えが配列形式で返ってくる。
n_c = output.expect[0]
n_a = output.expect[1]
例えば,output.expect[0]で一つ目のa.dag()*aの期待値を計算してくれる。これを描写してみる。
fig, axes = plt.subplots(1, 1, figsize=(10,6))
axes.plot(tlist, n_c, label="Cavity_g2")
axes.plot(tlist, n_a, label="Atom excited state")
axes.legend(loc=0)
axes.set_xlabel('Time')
axes.set_ylabel('Occupation probability')
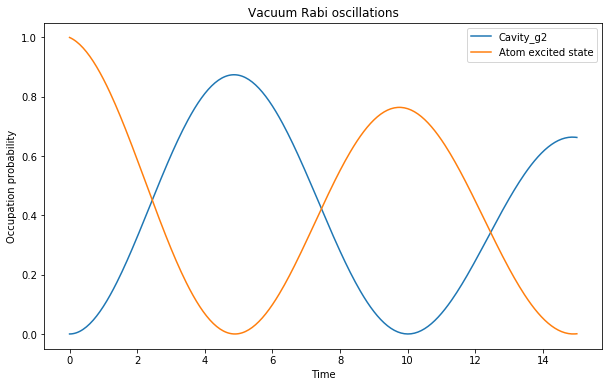
axes.set_title('Vacuum Rabi oscillations')
このようにラビ振動が計算できる。
ここまでだとただのコピペなので,一部変えてみる。例えば,結合定数gを大きくとったときに超強結合状態になるが,そのときには回転波近似が成り立たないと聞いた。つまり上のハミルトニアンが
\mathcal{H}=\hbar\omega_c a^\dagger a +\hbar\omega_a \sigma^\dagger \sigma+\hbar g (a^\dagger +a)(\sigma+\sigma^\dagger)
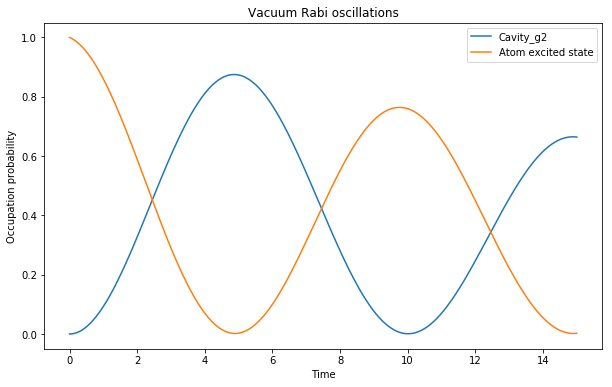
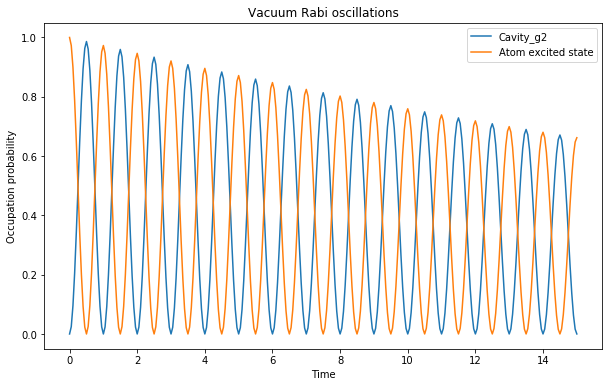
となるらしい。優位な差が出るのか検証してみる。現在g=0.05だが,これをg=0.5にしてみたときの差を比較する。
上との差は見られない。
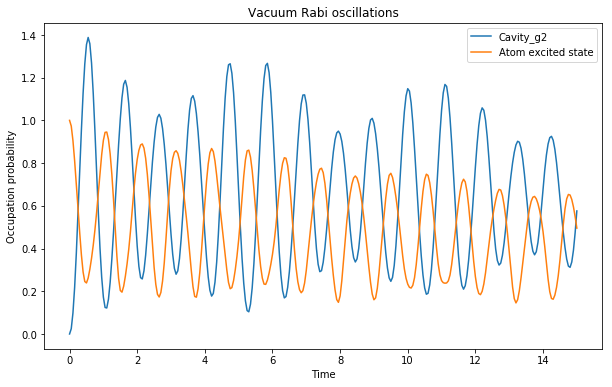
と結合定数が強い時の検証をしてみると優位な差が現れることがわかった。
他にもFock状態の初期値を変えて遊んでみたりとか色々できるはずなので,是非手にとって遊んでみて欲しい。