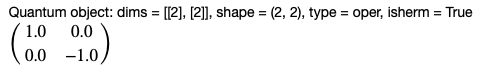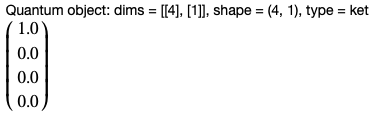QuTiP?
pythonの計算ライブラリで,第二量子化したハミルトニアンの計算がしやすいものです。
公式ページを見てみると,RIKENや学術振興会からサポートを受けているます。権威の傘を着るのはあまり好きではないですが,信頼性がありそうですね。
そもそも,このライブラリを使おうという研究者の方は英語が読めそうなので,ドキュメントの一部を日本語化した記事に需要があるかどうかは謎ですが,自分の備忘録として記載しておきます。
インストール
公式ドキュメントを読んでいると,pipとconda両方でのインストールは記述されていました。
pipであれば,
pip install qutip
condaであれば,
conda install -c conda-forge qutip
でインストールできます。
使い方
ここでの使い方は公式ドキュメントの資料のほとんどコピペです。
演算子の定義方法
QuTiPに計算させるObjectの作り方をまず説明します。
from qutip import Qobj
Qobjというクラスを使って計算対象のオブジェクトを作ります。
これを使うことで適当なケット(列)ベクトルを生成できます。
q = Qobj([[1], [0]])
と入力すると,jupyter notebook上では以下のような出力が得られます。
もちろんブラ(行)ベクトルに変更するのも簡単で,
q.dag()
と入力すると,出力が
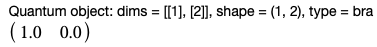
と得られます。つまり,ケット→ブラベクトルへの変換を数式から直感的に操作可能です。
試しに,
q.dag()*q
q*q.dag()
の計算を行ってみると,それぞれ
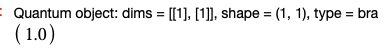
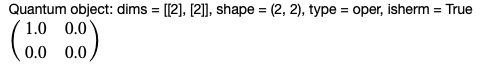
と計算できるので,簡単な記述でこれらの計算を行ってくれることがわかります。
さて,スピン2状態のみを考えたときにそのエネルギーを表すハミルトニアンは,
\mathcal{H}=\frac{\hbar\omega}{2}\sigma_z=\frac{\hbar\omega}{2}\{|+\rangle\langle +| - |-\rangle\langle -|\}
と記載されます。ここで,$|+\rangle$はエネルギーが高い方の状態,$|-\rangle$はエネルギーが低い方の状態,と定義します。また,先程定義したqは$|+\rangle$と一致します。
では,このハミルトニアンの演算子の部分($\sigma_z$)をQuTiPを使って定義してみましょう。
Qobjクラスは行列にも対応しており,以下のように定義することで,この演算子を定義することができます。
sigma_z = Qobj([[1,0],[0,-1]])
なので,あとはハミルトニアンを作るのであれば適当な係数をつければ良いだけなので簡単ですね。
他の系との相互作用を考えるのであれば,$\sigma_y$や$\sigma_x$が必要です。
複素数も簡単に定義できるので,$\sigma_y$を定義してみます。
sigma_y = Qobj([[0,-1j],[1j,0]])
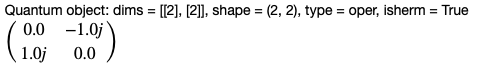
このように,-1jと書くことで複素数の定義も簡単に記述できます。
これら定義した演算子の次元は
hoge.dims
で確認できます。例えば,上で定義した$\sigma_y$に対してやってみましょう。
sigma_y.dims
[[2], [2]]
内部に定義されているクラスを使う
今までほQobjクラスをそのまま使っていましたが,よく利用される演算子についてはQuTiP内で定義されいることがあります。これらを使うとより簡単な記述で定義ができます。
二準位系の演算子
二準位系の状態ベクトルを記載するだけであれば,専用のクラスがあります。
例えば,$\sigma_z$と$\sigma_y$であれば,
from qutip import sigmay, sigmaz
sigma_y = sigmay()
sigma_z = sigmaz()
で上記と同じものが定義できます。
Fock stateの状態ベクトル
Fock stateという数状態の状態ベクトルを作ります。
Fock stateは例えばフォトンの数で基底を張る状態です。フォトンが1個であれば$|1\rangle$,10個であれば$|10\rangle$です。
from qutip import basis, fock
basis(4,2)
fock(4,2)
この2つであれば今はあまり差はありません。
両方同じ出力が得られます。
qobjクラスを使って頑張って定義してもよいですが,こちらのほうが簡単に定義できますね。
Fock状態の生成消滅演算子の行列もサポートされています。
from qutip import destroy,create
N = 4
a = destroy(N)
a_dag = create(N)
ここでNはFock状態の次元です。ヒルベルト空間上にどこまで基底を張るのかをここで定義しています。
さて,定義したaを出力してみると,
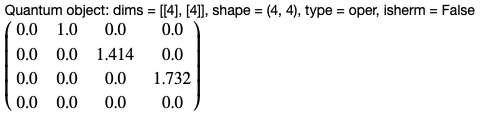
であるので,よくある文献と一致しています。便利ですね。
せっかくなので先程記述したFock状態ベクトルにここで定義した生成,消滅演算子を作用させてみましょう。
生成演算子
adag*fock(4,2)
a^\dagger|n\rangle = \sqrt{n+1}|n+1\rangle
であるので正しく計算ができていることがわかります。
消滅演算子
a*fock(4,2)
これも消滅演算子の定義から
a|n\rangle = \sqrt{n}|n-1\rangle
であるため,正しく計算できていることがわかります。
まとめ
今回はQuTiPでの計算を行うために,演算子の定義をいくつか行いました。
公式ドキュメントにより詳細は書かれているので,そちらを参照してください。
次は相互作用がある場合を考えて,もうちょっと面白い計算を行います。