【初心者向け】 移動ロボットのオドメトリ

#1. 概要
オドメトリとは，移動ロボットの変位を計算する手法の一種です．
この手法を用いて計算される変位そのものを指す場合もあります．

移動ロボットの車輪には車輪回転量が得られるエンコーダ(センサ)が付いており，それを用いてロボットの移動量を計算することができます．

用途としては主に以下が挙げられます．

• ロボットの自己位置推定
• スキャンマッチングにおける位置合わせの初期位置

こちらの記事では，変位の計算を数式ベースで理解し，c++の実装に落とし込むまでを解説します．

##目次
1. 概要
2. 条件
3. 座標系について
4. 変位の計算
5. ワールド座標系における変位の計算
6. オドメトリ計算の実装

#2. 条件

• ある瞬間(1フレーム)において，車輪の回転中心の位置は不変とします．
  ※車輪1個分の動きは円もしくは直線となります．

• ある瞬間(1フレーム)において，両輪の回転中心の位置は一致するとします．

• 計測される回転量は長さ単位として与えられるものとします．
  ※車輪が実際に転がった長さとします．
  ※角度回転量の場合は，車輪半径と掛け合わせる必要があります．

• 角度はラジアンとして与えられるものとします．

#3. 座標系について

##3.1. ロボット座標系

• ロボットに固定された座標系で，ロボットから周囲がどう見えるかを表現する際に用いられます．

• 今回は，$x$座標の正の向きはロボットの正面向きにとります．

• オドメトリの計算はロボット座標系で行う必要があります．

##3.2. ワールド座標系

• いわゆる普通の座標系で，ロボットの位置などはワールド座標系で表現されます．

#4. 変位の計算

ロボットがOにいる時点でのロボット座標系にて，ロボットがOからO'の地点まで変位する場合を考えます．
この時，左車輪位置はLからL'，右車輪位置はRからR'まで移動するものとします．

この時，各数式は

• $2d$: 車輪の間隔(定数)

• $r^l$: 左車輪の回転量

• $r^r$: 右車輪の回転量

となります．

ここで，各車輪とロボット位置の回転中心の位置Cは，L'，O'，R'を通る補助線を引くことによって，以下のように求まります．
また，これに伴って回転半径$\rho$が求まります．

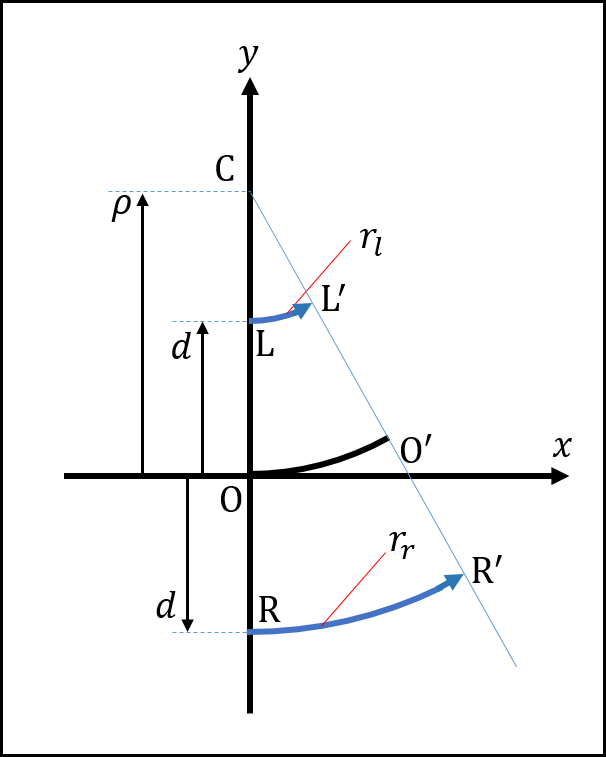
続いて，OO'の長さ$\Delta l$とロボットの回転角$\Delta \theta$を書き込みます．

ここで

\begin{align}
r_l = (\rho -d)\Delta \theta \\
r_r = (\rho +d)\Delta \theta 
\end{align}

より

\begin{align}
\Delta \theta = \frac{r_r-r_l}{2d} \tag{1}\\
\rho = \frac{r_r+r_l}{r_r-r_l} d \tag{2}

\end{align}

となります．

ある瞬間で回転中心が変わらないという条件より，OCとO'Cの長さは等しいので，OO'Cは二等辺三角形となります．
ここで，$\angle$OCO'を2等分する線を引くと，$\angle$O'O$x=\frac{\theta}{2}$となります．

ここで

\begin{align}
\Delta l = 2 \rho \sin \frac{\theta}{2} \tag{3}
\end{align}

となります．

ここまで来れば，ロボット座標におけるO'の座標$(\Delta x,\Delta y)$は

\begin{align}
\Delta x &= \Delta l \cos \frac{\theta}{2} \tag{4}\\
\Delta y &= \Delta l \sin \frac{\theta}{2} \tag{5}
\end{align}

となります．

以上の計算で，$(r_l,r_r)$から$(\Delta x, \Delta y, \Delta \theta)$を求めることができます．
※式の展開は省略します．

#5. ワールド座標系における変位の計算
これまでの計算で求めたオドメトリの変位$(\Delta x, \Delta y, \Delta \theta)$は，あくまでもロボット座標における変位です．
ワールド座標系における変位後の位置を考える際は，座標変換を考える必要があります．

各数式を

• O$(\Delta x, \Delta y, \Delta \theta)$: ロボット座標でのオドメトリ変位

• O$'(x_w,y_w,\theta_w)$: ワールド座標でのロボットの姿勢(変位前)

• $(x_w',y_w',\theta_w')$: ワールド座標でのロボットの姿勢(変位後)

とおきます．

変位前と後のロボット姿勢を示したものを以下に示します．

変位後のロボット姿勢を計算すると

\begin{align}
x_w' &= x_w + \cos \theta \cdot \Delta x 
- \sin \theta \cdot \Delta y \tag{6}\\
y_w' &= y_w + \sin \theta \cdot \Delta x 
+ \cos \theta \cdot \Delta y \tag{7}\\
\theta_w' &= \theta_w + \Delta \theta \tag{8}
\end{align}

となります．

以上の計算で，
$(\Delta x, \Delta y, \Delta \theta),(x_w,y_w,\theta_w)$から
$(x_w',y_w',\theta_w')$を求めることができます．

##5.1. 変位計算の補足1

ややくどい説明となりますが，cosやsinが出てくる部分について説明します．
(説明の要らない方は飛ばして下さい)
以下に先ほどの図を拡大したものを示します．

ここで，赤と青の直角三角形をそれぞれ書き込んでいます．
これらを補助線として活用することでピンクの線分の長さを算出でき，$x_w',y_w'$を求めることができます．

##5.2. 変位計算の補足2

$x,y$を$(2 \times 1)$の行列として扱っている場合は

\begin{eqnarray}

\left(
\begin{array}{}
x_w'\\
y_w'
\end{array}
\right)
&=&
\left(
\begin{array}{}
x_w + \cos \theta \cdot \Delta x - \sin \theta \cdot \Delta y \\
y_w + \sin \theta \cdot \Delta x + \cos \theta \cdot \Delta y
\end{array}
\right)\\
&=&
\left(
\begin{array}{}
x_w \\
y_w
\end{array}
\right)
+
\left(
\begin{array}{}
\cos \theta & - \sin \theta \\
\sin \theta &   \cos \theta
\end{array}
\right)
\left(
\begin{array}{}
\Delta x \\
\Delta y
\end{array}
\right) \\
\theta_w' &=& \theta_w + \Delta \theta
\end{eqnarray}

という式に変形できます．
ここで

\left(
\begin{array}{}
\cos \theta & - \sin \theta \\
\sin \theta &   \cos \theta
\end{array}
\right)
=
R_\theta

は回転行列と呼ばれています．

#6. オドメトリ計算の実装

c++にて，

• 車輪回転量からオドメトリ変位(ロボット座標系)を計算する関数
• オドメトリ変位(ロボット座標系)から変位後のロボットの姿勢(ワールド座標系)を計算する関数

をそれぞれ実装していきます．

main.cpp

#include<iostream>

#define M_PI 3.141592

using namespace std;

typedef struct Pose_2D
{
	float X;
	float Y;
	float Yaw;
} Pose_2D;

void getOdometryDisplacement(const float r_left, const float r_right, Pose_2D &delta_odometry)
{
	const float d_width = 0.05;
	float rho_rotationCenter;
	float delta_l;

	if (r_left == r_right)
	{
		//output
		delta_odometry.X = r_left;
		delta_odometry.Y = 0.;
		delta_odometry.Yaw = 0.;
		return;
	}

	delta_odometry.Yaw = 0.5 * (r_right - r_left) / d_width;

	rho_rotationCenter = (r_left + r_right) / (r_right - r_left) * d_width;

	delta_l = 2. * rho_rotationCenter * sin(0.5 * delta_odometry.Yaw);

	//output
	delta_odometry.X = delta_l * cos(0.5 * delta_odometry.Yaw);
	delta_odometry.Y = delta_l * sin(0.5 * delta_odometry.Yaw);
	return;
}

void getPoseAfterOdometry(const Pose_2D delta_odometry, const Pose_2D pose_before_w, Pose_2D &pose_w)
{
	pose_w.X = pose_before_w.X + cos(pose_before_w.Yaw) * delta_odometry.X - sin(pose_before_w.Yaw) * delta_odometry.Y;
	pose_w.Y = pose_before_w.Y + sin(pose_before_w.Yaw) * delta_odometry.X + cos(pose_before_w.Yaw) * delta_odometry.Y;
	pose_w.Yaw = pose_before_w.Yaw + delta_odometry.Yaw;
	return;
}

int main()
{
	//variable
	float r_left, r_right;
	r_left = 0.4;
	r_right = 0.45;
	Pose_2D pose_before_w;
	pose_before_w.X = 1.;
	pose_before_w.Y = 0.;
	pose_before_w.Yaw = 30. * M_PI / 180.;

	//result variable
	Pose_2D pose_w;

	cout << "Pose: (X, Y, Yaw) = (";
	cout << pose_before_w.X << " ,";
	cout << pose_before_w.Y << ", ";
	cout << pose_before_w.Yaw << ")" << endl;
	cout << endl;

	cout << "Input(Odometory): (r_l, r_r) = (";
	cout << r_left << ", ";
	cout << r_right << ")" << endl;
	cout << endl;

	cout << "start calculation" << endl;
	cout << endl;
	Pose_2D delta_odometry;
	getOdometryDisplacement(r_left, r_right, delta_odometry);
	getPoseAfterOdometry(delta_odometry, pose_before_w, pose_w);

	cout << "Displacement(Odometory): (X, Y, Yaw) = (";
	cout << delta_odometry.X << " ,";
	cout << delta_odometry.Y << ", ";
	cout << delta_odometry.Yaw << ")" << endl;
	cout << endl;

	cout << "Pose: (X, Y, Yaw) = (";
	cout << pose_w.X << " ,";
	cout << pose_w.Y << ", ";
	cout << pose_w.Yaw << ")" << endl;
	cout << endl;

	return 0;
}

実行結果

Pose: (X, Y, Yaw) = (1 ,0, 0.523599)

Input(Odometory): (r_l, r_r) = (0.4, 0.45)

start calculation

Displacement(Odometory): (X, Y, Yaw) = (0.407512 ,0.104055, 0.5)

Pose: (X, Y, Yaw) = (1.30089 ,0.29387, 1.0236)

#まとめ
今回は，オドメトリの変位計算を図式的に解説し，c++にてその手順をプログラムの形で実装しました．

内容に関してお気付きの点があれば気軽にお問い合わせ下さい．