年金の係数とは
年金で将来の積立額を簡易的に計算するための係数があったりします。
●定期預金のように利息がつく場合に将来いくらになるかや今いくらあればよいか知りたいときに用いる係数
●年金のように、毎月少しずつ積み立てて、将来少しずつ取り崩す場合の金額を知りたいときに用いる係数
- 毎月1万円ずつ積み立てたら10年後いくらになるか知りたいとき→年金終価係数
- 10年後に10万円貯めるために毎月いくら積み立てればよいか知りたいとき→減債基金係数
- 10年間毎月1万円ずつ取り崩すのに今いくらあればよいか知りたいとき→年金現価係数
- 今10万円あって10年間で取り崩すのに毎月いくら使えるかしりたいとき→資本回収係数
お約束:免責事項など
- 本投稿は年金制度の話ではありません。年金制度の内容は必ず厚生労働省または日本年金機構のHPで確認してください。
- 本投稿での計算及び計算した数値は仮定のものであり、その数値に一切責任は負いません。
- 本内容は2018年7月29日時点のものです。
- 本内容は個人の見解であり、所属組織とは一切関係ありません。
- もし誤った記載がありましたら、修正・削除しますので、ご指摘ください。
終価係数
10万円を年利回り1%の定期預金に10年間預けたとき、10年後いくらになるか計算してみます。
$$100000 \times (1+0.01)^{10}$$
print(int(100000 * (1+0.01)**10))
110462
一般に、現在の預金$A$円、年利回り$r$、期間$T$年としたとき、$T$年後の預金額$F$は、
$$F=A(1+r)^T$$
となります。このとき、
$$SPCAF=(1+r)^T$$
を終価係数(Single Payment Compound Amount Factor)と呼びます。
年利回り1%、10年間の終価係数は、
def spcaf(r, T):
return (1+r)**T
print(spcaf(0.01, 10))
1.1046221254112045
となります。
現在の預金額$A$としたときの$T$年後の預金額$F$は、
$$F = SPCAF \times A$$
と書くことができます。
終価係数を用いると、
A = 100000
print(int(A * spcaf(0.01, 10)))
110462
というように計算することもできます。
現価係数
年利回り1%の定期預金で10年後に10万円貯めるために、今いくら預ければよいか計算してみます。
$$100000 \times \frac{1}{(1+0.01)^{10}}$$
print(int(100000*(1/(1+0.01)**10)))
90528
一般に、期間$T$年、年利回り$r$、$T$年後の預金$F$としたとき、現在の預金額$A$は、
$$A=\frac{1}{(1+r)^T}F$$
となります。このとき、
$$SPPWF=\frac{1}{(1+r)^T}$$
を現価係数(Single Payment Present Worth Factor)と呼びます。
年利回り1%、10年間の現価係数は、
def sppwf(r, T):
return 1/(1+r)**T
print(sppwf(0.01, 10))
0.9052869546929833
となります。
$T$年後の預金額$F$としたときの現在の預金額$A$は、
$$A=SPPWF \times F$$
と書くことができます。
現価係数を用いると、
F = 100000
print(int(F * sppwf(0.01, 10)))
90528
と計算することもできます。
現価係数と終価係数には、
$$SPPWF=\frac{1}{SPCAF}$$
という関係があります。
現価係数は、債券や資産運用の分野では、ディスカウント・ファクター(割引係数)と呼んだりします。
年金終価係数
年金のために、毎期1万円ずつ積み立てることを考えます。最初の3年間を表にしてみます。利率は1%で毎期末に1万円積み立てます。
| 時点 | 前期末資産 | 利率 | 積立前の期末資産 | 期末積立 | 積立後の期末資産 |
|---|---|---|---|---|---|
| 1 | 0 | 0.01 | 0 | 10000 | 10000 |
| 2 | 10000 | 0.01 | 10100 | 10000 | 20100 |
| 3 | 20100 | 0.01 | 20301 | 10000 | 30301 |
毎期の積立額$x$、利率$r$とすると、以下のように一般化できます。
| 時点 | 前期末資産 | 利率 | 積立前の期末資産 | 期末積立 | 積立後の期末資産 |
|---|---|---|---|---|---|
| 1 | $0$ | $r$ | $0$ | $x$ | $x$ |
| 2 | $x$ | $r$ | $x(1+r)$ | $x$ | $x(1+r)+x$ |
| 3 | $x(1+r)+x$ | $r$ | $x(1+r)^2+x(1+r)$ | $x$ | $x(1+r)^2+x(1+r)+x$ |
よって、$T$時点での積立後の期末資産の総額$S_T$(元利合計額)は
$$S_T= \sum_{t=1}^T x(1+r)^{t-1}$$
となります。
$T$が大きくなると手で計算するのは大変です。一応、以下のようにfor文でも計算もできます。
T = 10
S_T = 0
for t in range(T):
S_T += 10000 * (1+0.01)**t
print(int(S_T))
104622
総額$S_T$は等比数列の和の形式をしています。$1+r$を掛けたものと引き算をすると、
\begin{eqnarray}
S_T &=& x + && x(1+r) + \cdots + x(1+r)^{T-1} &&\\
(1+r)S_t &=& && x(1+r) + \cdots + x(1+r)^{T-1} && + x(1+r)^T\\
-rS_t &=& x && && - x(1+r)^T
\end{eqnarray}
となります。よって、
\begin{eqnarray}
S_t &=& \frac{-x + x(1+r)^T}{r}\\
&=& \frac{(1+r)^T-1}{r}x\\
\end{eqnarray}]
となります。このとき、
$$USCAF=\frac{(1+r)^T-1}{r}$$
を年金終価係数(Uniform Series Compound Amount Factor)と呼びます。
利回り1%、10年間の年金終価係数は
def uscaf(r, t):
return ((1+r)**t-1)/r
print(uscaf(0.01, 10))
10.462212541120453
となります。
毎年の積立額$X$としたとき、$T$年後の積立総額$S_T$は
$$S_T=USCAF \times X$$
と書くことができます。
年金終価係数を用いると、
x = 10000
S_T = uscaf(0.01, 10) * x
print(int(S_T))
104622
と簡単に計算することもできます。
減債基金係数
10年後に10万円貯めるために、毎年いくら積み立てればよいか考えます。これはすでに年金終価係数のところで計算しています。
$$S_T=\frac{(1+r)^T-1}{r}x$$
より
$$x=S_T\frac{r}{(1+r)^T-1}$$
となります。このとき、
$$SFF=\frac{r}{(1+r)^T-1}$$
を減債基金係数(Sinking Fund Factor)と呼びます。
利回り1%、10年間の減債基金係数は
def sff(r, T):
return r/((1+r)**T-1)
print(sff(0.01, 10))
0.09558207655117135
となります。$T$年後の積立総額$S_T$としたとき、毎年の積立額$X$は
$$X=SFF \times S_T$$
と書くことができます。
減債基金係数を用いると
S_T = 100000
x = sff(0.01, 10) * S_T
print(int(x))
9558
と計算できます。
年金現価係数
年金として、10年間に毎期1万円ずつ取り崩すことを考えます。最初の3年間を評にしてみます。利率は1%で毎期末に1万円取り崩します。
| 時点 | 前期末資産 | 利率 | 受給前の期末資産 | 期末年金 | 受給後の期末資産 |
|---|---|---|---|---|---|
| 1 | 100000 | 0.01 | 101000 | 10000 | 91000 |
| 2 | 91000 | 0.01 | 91910 | 10000 | 81910 |
| 2 | 81910 | 0.01 | 82729 | 10000 | 72729 |
年金原資$S$、毎期の積立額$x$、利率$r$とすると、以下のように一般化できます。
| 時点 | 前期末資産 | 利率 | 受給前の期末資産 | 期末年金 | 受給後の期末資産 |
|---|---|---|---|---|---|
| 1 | $S$ | $r$ | $S(1+r)$ | $x$ | $S(1+r)-x$ |
| 2 | $S(1+r)-x$ | $r$ | $S(1+r)^2-x(1+r)$ | $x$ | $S(1+r)^2-x(1+r)-x$ |
| 3 | $S(1+r)^2-x(1+r)-x$ | $r$ | $S(1+r)^3-x(1+r)^2-x(1+r)$ | $x$ | $S(1+r)^3-x(1+r)^2-x(1+r)-x$ |
よって、$T$期間に毎期1万円ずつ取り崩すために必要な年金原資$S_0$は
$$(S_0-x)(1+r)^T - x(1+r)^{T-1}-\cdots -x(1+r)-x=0$$
を解くことで求めることができます。これを解くと、
$$\Leftrightarrow (S_0-x)(1+r)^T =x(1+r)^{T-1}+\cdots -x(1+r)-x$$
$$\Leftrightarrow S_0-x =\frac{1}{1+r}x+\cdots +\frac{1}{(1+r)^{T-1}}x+\frac{1}{(1+r)^T}x$$
$$\Leftrightarrow S_0 =x+\frac{1}{1+r}x+\cdots +\frac{1}{(1+r)^{T-1}}x+\frac{1}{(1+r)^T}x$$
より、
$$S_0 = \sum_{t=1}^T \frac{1}{(1+r)^t}x$$
となります。
年金原資$S_0$は等比数列の和の形式をしています。(なお、等比数列の和の計算を用いた年金現価係数の計算は年金終価係数の計算と全く同じです。)$1+r$を掛けたものと引き算をすると、
\begin{eqnarray}
S_0 &=& &&\frac{1}{1+r}x+\cdots +\frac{1}{(1+r)^{T-1}}x&&+\frac{1}{(1+r)^T}x \\
(1+r)S_0 &=& x+&& \frac{1}{1+r}x+\cdots +\frac{1}{(1+r)^{T-1}}x &&\\
-rS_0 &=& -x&& &&+ \frac{1}{(1+r)^T}x \\
\end{eqnarray}
となります。よって、
\begin{eqnarray}
S_0 &=& \frac{1}{r}(x- \frac{1}{(1+r)^T}x)\\
&=& \frac{1}{r}(1- \frac{1}{(1+r)^T})x\\
&=& (\frac{(1+r)^T-1}{r(1+r)^T})x\\
\end{eqnarray}
となります。このとき、
$$USPWF=\frac{(1+r)^T-1}{r(1+r)^T}$$
を年金現価係数(Uniform Series Present Worth Factor)と呼びます。
利回り1%、10年間の年金現価係数は
def uspwf(r, T):
return ((1+r)**T-1)/(r*(1+r)**T)
print(uspwf(0.01, 10))
9.471304530701673
となります。$T$年間の毎年の取り崩し額$X$としたとき、年金原資$S_0$は
$$S_0=USPWF \times X$$
と書くことができます。
年金現価係数を用いると、
x = 10000
S_0 = uspwf(0.01, 10) * x
print(int(S_0))
94713
と簡単に計算できます。
資本回収係数
年金原資10万円を10年間で取り崩すとき、毎期いくらずつ使えるか考えます。すでに年金現価係数で計算したものを用いることができます。
$$S_0 =(\frac{(1+r)^T-1}{r(1+r)^T})x$$
より
$$x=\frac{r(1+r)^T}{(1+r)^T-1}S_0$$
となります。このとき、
$$CRF=\frac{r(1+r)^T}{(1+r)^T-1}$$
を資本回収係数(Capital Recovery Factor)と呼びます。
利回り1%、10年間の資本回収係数は
def crf(r, T):
return (r*(1+r)**T)/((1+r)**T-1)
print(crf(0.01, 10))
0.10558207655117136
となります。年金原資$S_0$としたとき、$T$期間での毎年の取り崩し額$X$は
$$X=CRF \times S_0$$
と書くことができます。
資本回収係数を用いると
S_0 = 100000
x = crf(0.01, 10) * S_0
print(int(x))
10558
と計算できます。
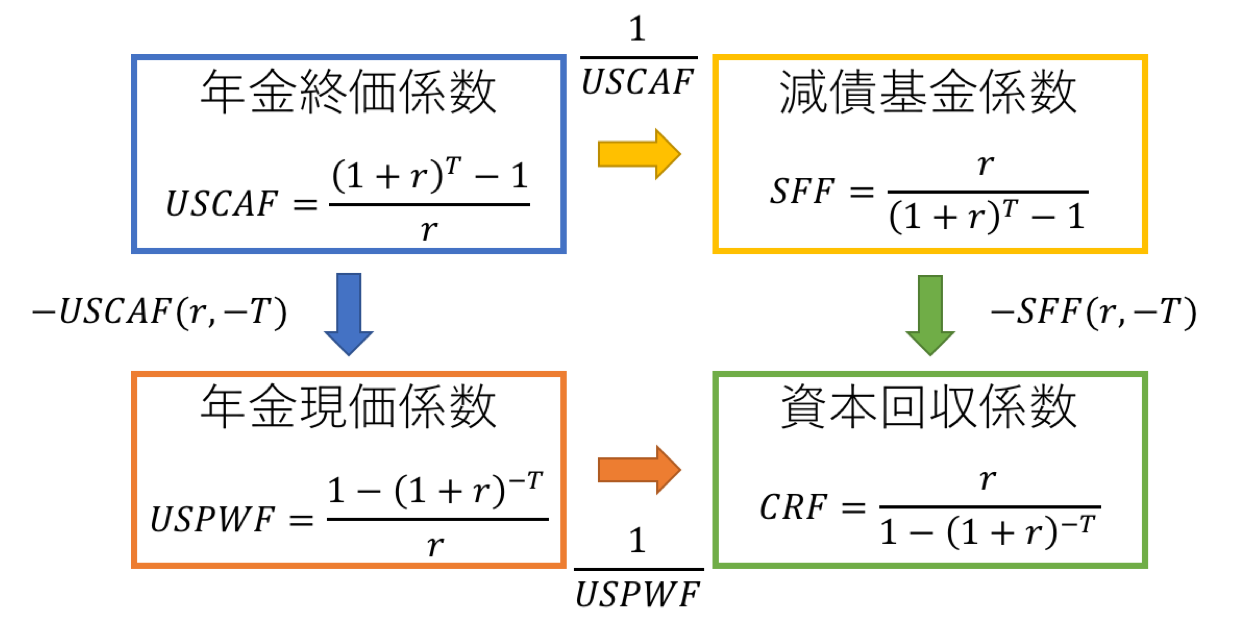
係数のまとめ
年金に関する係数の関係をまとめます。どれか一つだけ覚えておけば、他のケースにも対応できると思います。
class PensionFactor():
def __init__(self, r, t):
self.r = r
self.t = t
# 終価係数
def spcaf(self):
return (1+self.r)**self.t
# 現価係数
def sppwf(self):
return 1/spcaf(self.r, self.t)
# 年金終価係数
def uscaf(self):
return ((1+self.r)**self.t-1)/self.r
# 減債基金係数
def sff(self):
return 1/uscafself.r, self.t)
# 年金現価係数
def uspwf(self):
return -uscaf(self.r, -self.t)
# 資本回収係数
def crf(self):
return -1/uscaf(self.r, -self.t)
pf = PensionFactor(0.01, 10)
print('終価係数:', pf.spcaf(),
'\n現価係数:', pf.sppwf(),
'\n年金終価係数:', pf.uscaf(),
'\n減債基金係数:', pf.sff(),
'\n年金現価係数:', pf.uspwf(),
'\n資本回収係数:', pf.crf())
終価係数: 1.1046221254112045
現価係数: 0.9052869546929833
年金終価係数: 10.462212541120453
減債基金係数: 0.09558207655117135
年金現価係数: 9.471304530701675
資本回収係数: 0.10558207655117133
係数を使う際の注意点
係数は簡易的に見積もる場合には便利ですが、以下のような問題点があります。
- 毎年の積立額が固定
- 利回りが固定
- 税金を考慮していない
毎年の積立額は自分の意思でコントロールできる変数です。
利回りは、利率が確定している場合は係数が使えますが、確定拠出年金のように利回りが運用によって変わる場合には、不確実性があるので、単純な計算では見積もりにくくなります。
税金は自身の所得によっても変わる場合もあります。また、税制が変わる可能性もありますが、いきなり変わるものではないので、改正があれば事前に再計算もできます。利回りよりは考慮しやすい気がします。そのうち税金を考慮した積立額計算はやってみたいと思います。
参考になりそうなもの
- ファイナンシャル・プランニング技能検定のテキスト(あまり詳しくないですが)
- 年金アクチュアリーのテキスト?(読んだことないですが)
- Pythonで国民年金シミュレーション(その2)(直接関係ないですが以前書いたもの)