はじめに
機械学習は面白く、夢の広がる技術であるにも関わらず、手を出そうとしないエンジニアがとても多いと感じていました。私もはじめは「機械学習?取り敢えず学習はするんだろうけど全然イメージが付かないし使えるかも分からない」とこの技術に関してあまり興味を持っていませんでしたが、ある時なんとなく「機械学習でも少し調べてみるか」とCoursera内にあるAndrew Ng氏によるMachine Learningのコースの動画を見ていて「これは滅茶苦茶夢のある技術だ」とみるみるハマっていき、そこで本格的に「勉強してみよう」という気になりました。
アンドリュー・ン(英語: Andrew Ng、中国語: 吳恩達、1976年4月18日 - )は、中国系アメリカ人の計算機科学者、人工知能研究者、投資家、起業家、Google Brain(英語版)の共同設立者、 Baiduの元副社長兼チーフサイエンティスト、スタンフォード大学 兼担教授である。EラーニングサービスのCourseraとdeeplearning.aiとAI Fundの創始者でもある[2]。
機械学習は面白い、しかしそれを学ぼうとするエンジニアは少ない。私が思うに機械学習をやろうとしないのは「処理内容が全くイメージが付かないから」なんだと思います。だから、この記事によって最低限「機械学習完全に理解した」という状態に持っていけるくらいに分かりやすくかつ十分な情報を持ってして機械学習というものを説明しようと思います。
この記事で得られること
- 機械学習のアルゴリズムが分かる
- 機械学習を一から実装出来るようになる
機械学習を理解する
機械学習の定義
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
コンピュータプログラムがタスクのクラスTと性能指標Pに関し経験Eから学習するとは、T内のタスクのPで測った性能が経験Eにより改善される事を言う
分かりやすくいうと、あるタスクとタスクの性能指標があるとして、経験(例えば、訓練データ)から学習して、その性能指標で測った時に性能が上がっていればそれは機械学習と言いますよ、ということです。
二つの実装方法
機械学習と聞いても「学習ってなんだろう。そもそも学習の結果として何があるのだろう」と、情報のヒントなしでは中々イメージがし辛いです。イメージを持ってもらうために以下で簡単に説明します。
※ Courseraで説明される図とは若干異なり、理解しやすさ重視でより簡単な図にしています。
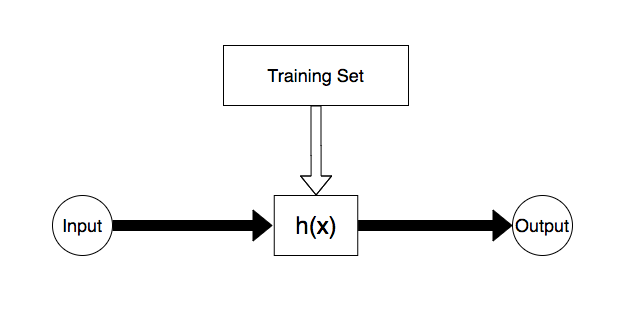
関数実装に関して、二つの実装方法があると考えると分かりやすいです。
一つはエンジニアが自分達の手で実装
一つは訓練データで実装
訓練データによる実装は「CSVを挿入すれば自動的にアウトプットの値が正しい値に近付く」というイメージです(反感を買いそうな表現ではありますが)
具体例で理解する
| x1 | x2 | x3 | AND |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
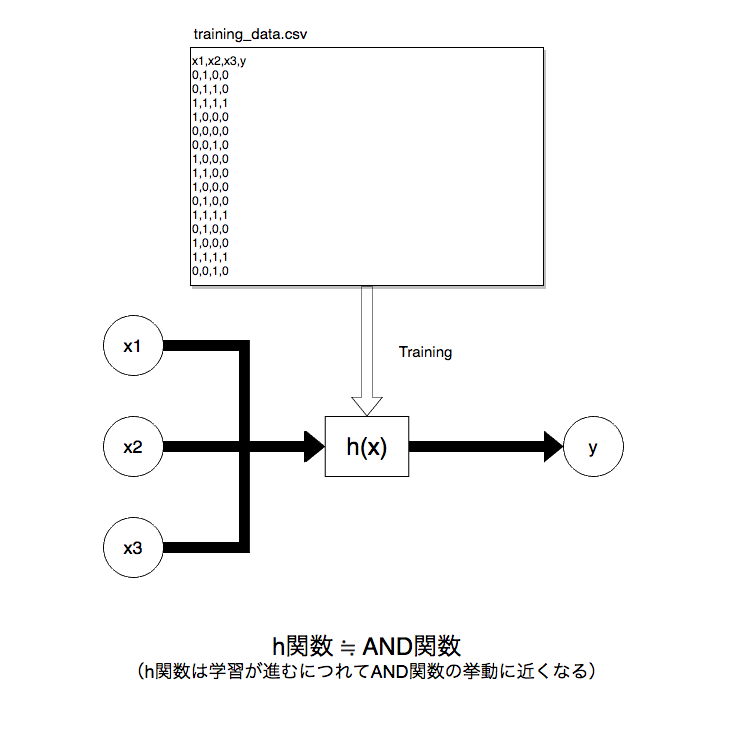
AND関数というものを実装したいとします。
引数としてx1, x2, x3をとり、上記の真理値表の通り入力が全て1である場合にのみ1(真)を出力するというものです。
以下のように手元に用意しておいた正解ラベル付き訓練データtraining_data.csvで学習させます。
(※ 以下のyの列が正解ラベル)
学習が進むと、内部で自動的に**機械が持つパラメーター(後述)**が正しい値にチューニングされ、ANDモデルが構築されます。こうして出来上がった仮設関数h(x)を、後は以下のように値を入れて使うだけです。
result = h(1, 0, 1)
print(result) # <--- 0 (正解)
result = h(1, 1, 1)
print(result) # <--- 1 (正解)
result = h(0, 1, 1)
print(result) # <--- 1 (不正解)
理論
概要
機械学習の数式を理解します。これを理解すれば機械学習がどのように処理しているのかが分かるようになり、機械学習というものをよりイメージしやすくなります。
知識的準備
シグマ
n = 繰り返す回数 \\
i = スタートの値 \\
\sum_{i=1}^n\bigl(i + 2\bigl) \\
機械学習では上記のような数式が登場します(シグマと言います)。はじめは拒否反応を起こすかもしれませんが、実際には、開発経験者かつ足し算引き算などの四則演算が分かっていればそんなに難しくはないです。なぜならforループと考え方がほぼ同じだからです(機械学習の数式についても一つ一つ紐解くので安心してください)
n = 3 である時 \\
\sum_{i=1}^n\bigl(i + 2\bigl) = (1 + 2) + (2 + 2) + (3 + 2) = 12
シグマではイテレーション毎に出た値を足します。
念のため伝えると、下記のように掛け算で繋げるものもあり、π(パイ)の大文字が記号として使われます。
n = 3 である時 \\
\prod_{i=1}^n\bigl(i + 2\bigl) = (1 + 2) \times (2 + 2) \times (3 + 2) = 60
これで準備は以上です。
機械学習の数式・用語
機械学習では、以下の数式が登場します。
後で一つ一つ分解して説明するので、今は軽く眺める程度で大丈夫です。
重み(Weight)
\theta \\
(書籍によってはWで表される)
損失関数(Loss Function)
J(\theta)
平均二乗誤差(Mean Squared Error)
J(\theta_j) = \frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
\frac{d}{d \theta_j} J(\theta_j) = \frac{1}{n} \sum_{i = 1}^{n} \Bigl( h(x^{(i)}) - y^{(i)} \Bigl)X^{(i)}_j
仮設関数(Hypothesis Function)
h(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_j x_j = 予測した値
最急降下法 (勾配降下法, Gradient Descent)
\theta_j = \theta_j - a \frac{d}{d \theta_j}J(\theta_j)
機械学習アルゴリズムを理解する
例として「家の大きさで価格を予測するモデル」で流れを説明しようと思いますが、
その前にグラフについて説明します。
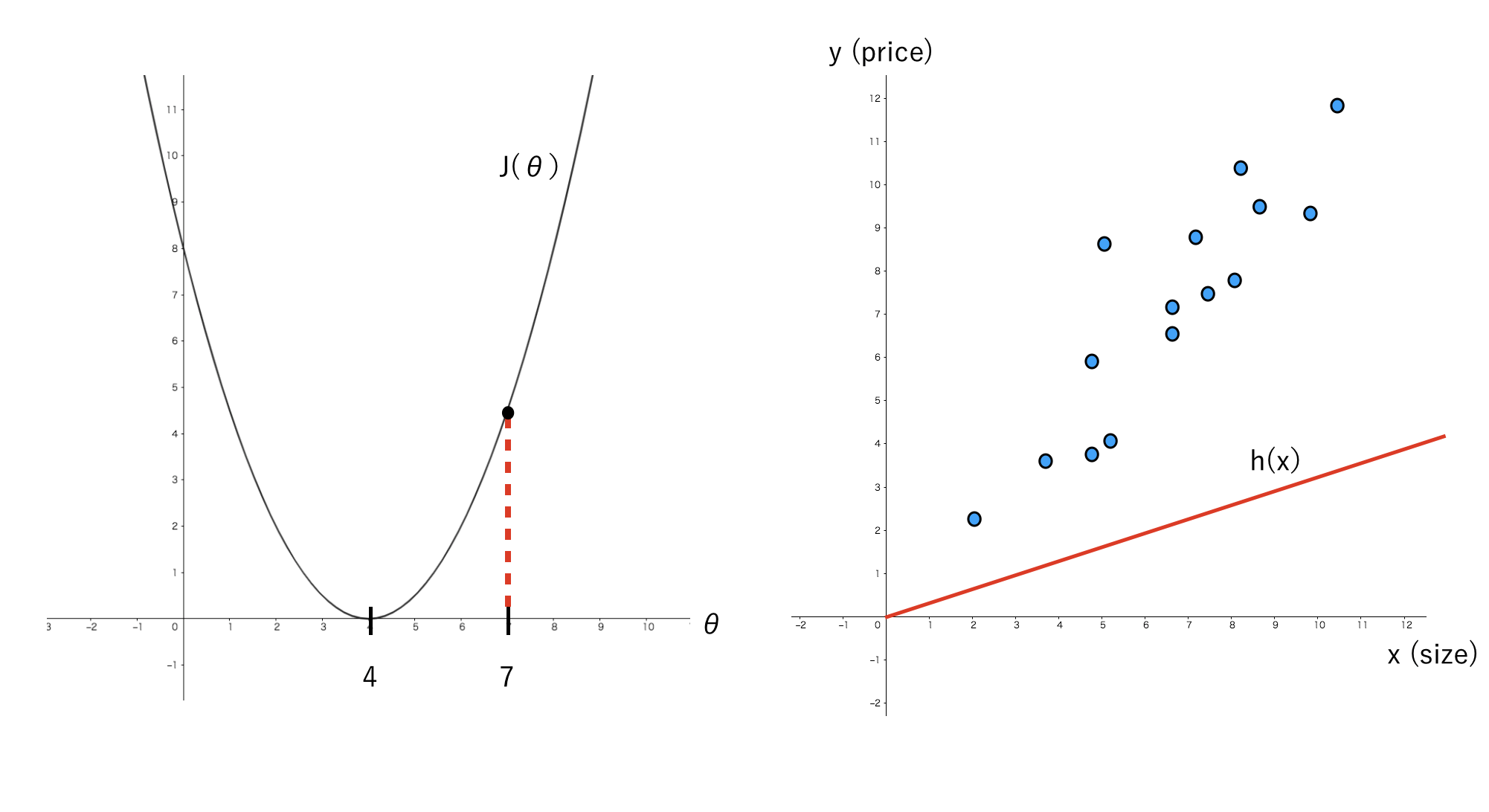
グラフの説明
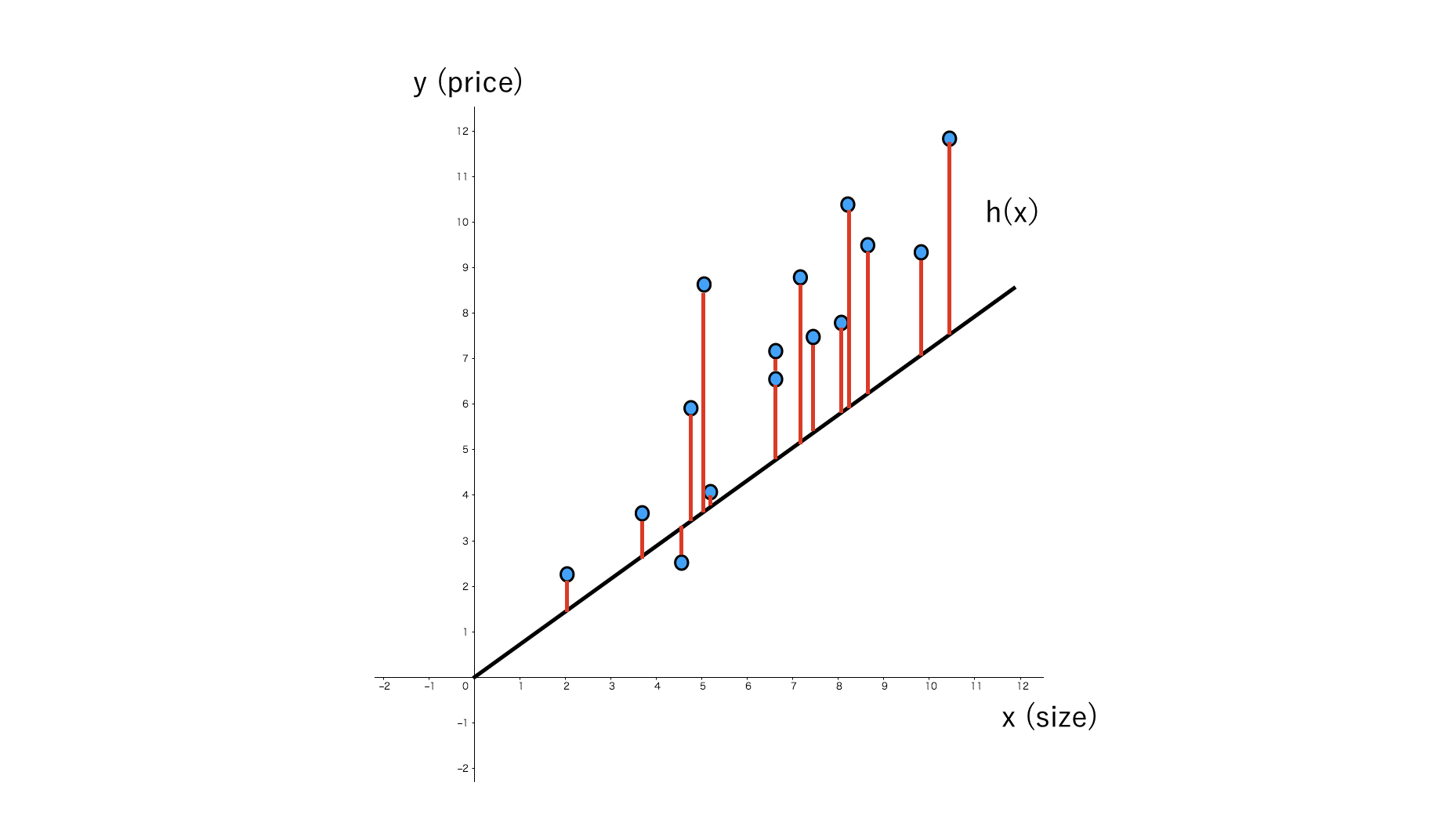
左図はJ(θ)とθの関係性を表し、右図は実際のデータ、x(size)とy(price)の関係性を表しています。
x: size
この例では家の大きさを表します。
y: price
家の値段を表します。
θ: シータ
θは「シータ」と読み、学習をするたびに予測するに最適な値へと自動的に変化します。機械が持つ変数だと考えると分かりやすいかもしれません。機械学習において非常に重要なパラメーターです。
J(θ): 損失関数
J(θ)は損失関数(または誤差関数、目的関数でも良い)と言い、θをJ関数のインプットといて入れた場合「実際のデータとどのくらい誤差があったか」を示し、この値が低ければ低い程誤差が少なくて良いということになります。
h(x): 仮設関数
h(x)は仮設関数と呼ばれるもので、前述の通り、学習後はこれを用いて予測をすることになります。
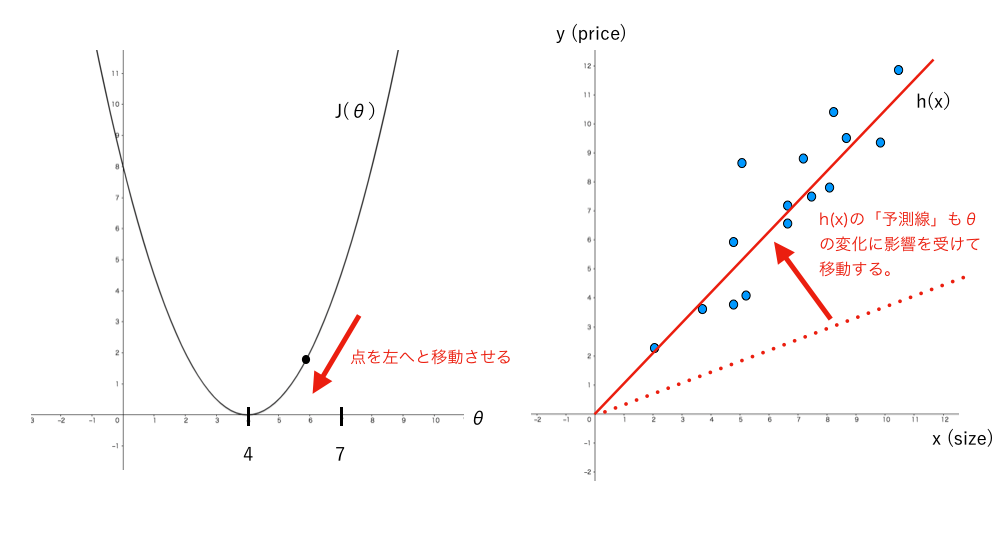
学習の目的
学習が進むとJ(θ)上にある点が段々と下がっていき、最終的には一番下まで行き、収束します。その時点でh(x)の「予測線」もθの変化の影響を受けて実際のデータに近い位置まで移動しています。
この「J(θ)の軌道上にある点を一番下まで移動させ、モデルの予測精度を上げること」が機械学習の目的になります。
数式の説明
それでは、前述した数式について分解して説明します。
\begin{align}
J(\theta_j) = \frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2 ・・・・・・・・・・・・ 1 \\
\newline
\newline
\frac{d}{d \theta_j} J(\theta_j) = \frac{1}{n} \sum_{i = 1}^{n} \Bigl( h(x^{(i)}) - y^{(i)}
\Bigl)X^{(i)}_j ・・・・・・・・・・・ 2 \\
\newline
\newline
h(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_j x_j ・・・・・・・・・・ 3 \\
\newline
\newline
\theta_j = \theta_j - \frac{d}{d \theta_j}J(\theta_j) ・・・・・・・・・・・・・・・・・・・ 4 \\
\end{align}
平均二乗誤差
数式と名前は物々しいですが、やっていることは単純です。
J(\theta_j) = \frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
この式を軽く説明すると「予測した家の値段(h(x))と実際の家の値段(y)の差を二乗してその誤差を平均する」となります。
これを分解して見ましょう。
h(x) - y
x(家の大きさ)をh関数のインプットとして入力し、出力として予測した値(家の値段)が返って来ます。
予測した値と実際のデータとどのくらい誤差があったかを計算しています。
\sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)
シグマは前述した通り「forループ」のようなもので、算出した誤差を合算しています。
(上図の赤線が予測線との誤差)
\sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
誤差の合計に二乗している理由は、誤差を合算させた結果を「マイナスの値にしないため」です。
二乗すれば例え誤差合計が-3だとしても(-3) * (-3) = 9となり、マイナスの値にはなりません。
\frac{1}{n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
N(データの数)で割り、平均を算出しています。
\frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
1/2nとなっている理由は、「2を付けておけば微分をした際に打ち消されて綺麗な数式になるから」です。
(実際に使用する式はこれに微分した式であるため)
J(\theta) = \frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2
これが平均二乗誤差です。
\begin{align}
\newline
\frac{d}{d \theta} ・・・・・・・・・・・・・・・・・・ 1 \\
\frac{d}{d \theta} J(\theta) ・・・・・・・・・・・・・・・ 2
\newline
\newline
\end{align}
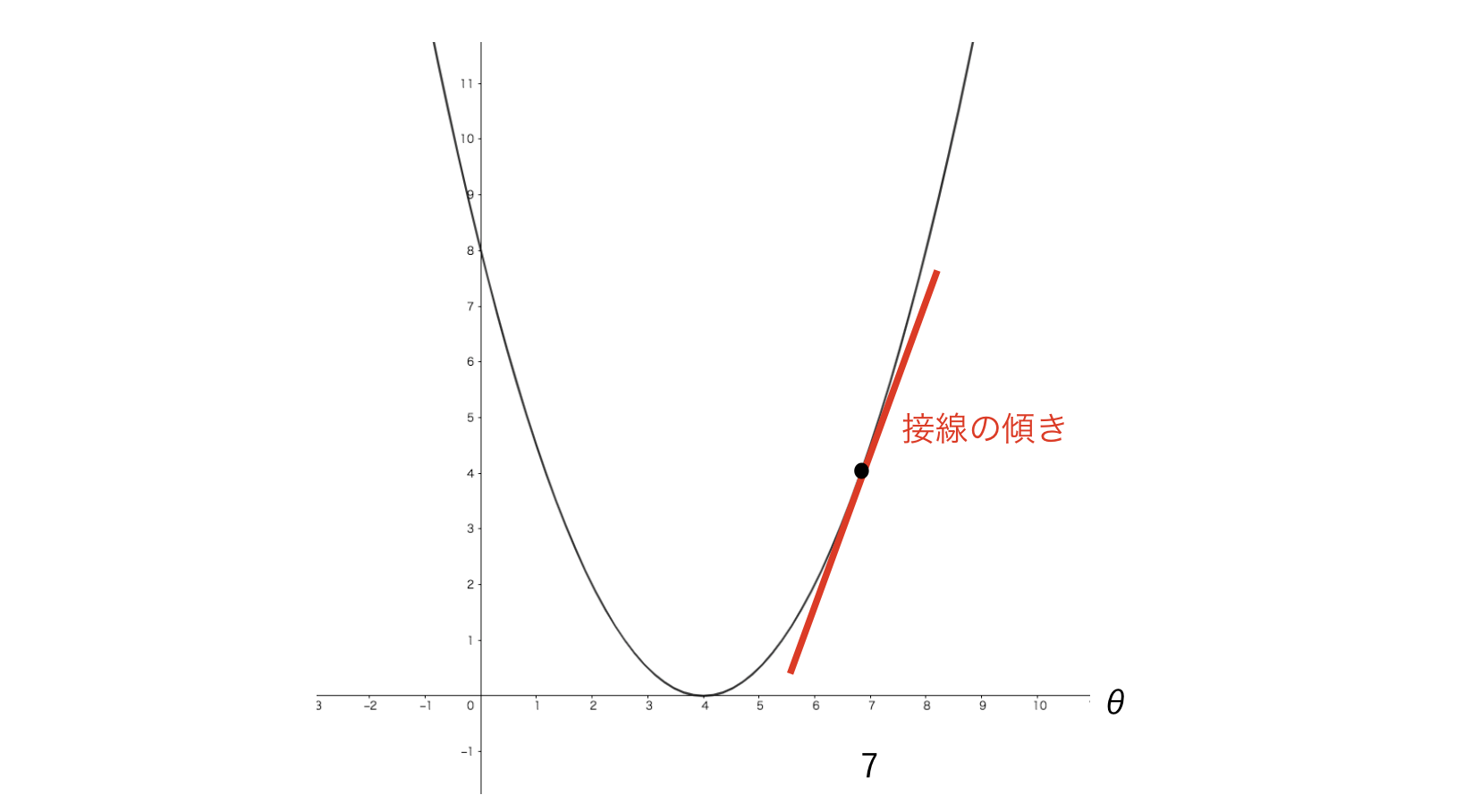
2は「J(θ)をθで微分する」と読みます。
1は難しそうな記号に見えますが、機械学習のために微分を覚える必要はなく「微分をすると接線の傾きを求められるんだな」程度の理解で問題ありません。(傾きを求めるのは「θを更新する際の方向」が分かるため非常に重要です)
J(\theta) = \frac{1}{2n} \sum_{i=1}^{n} \Bigl(h(x^{(i)}) - y^{(i)} \Bigl)^2 ・・・・・・ before\\
\frac{d}{d \theta} J(\theta) = \frac{1}{n} \sum_{i = 1}^{n} \Bigl( h(x^{(i)}) - y^{(i)}
\Bigl)X^{(i)} ・・・ after
J(θ)をθで微分すると上のような式になります。
仮設関数
仮設関数について説明します。
\begin{align}
\newline
h(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_j x_j
\newline
\newline
\end{align}
「家の大きさ」などの特徴がj個ある場合はこのような
\begin{align}
\newline
h(x) = \theta_0 + \theta_1 x_1
\newline
\newline
\end{align}
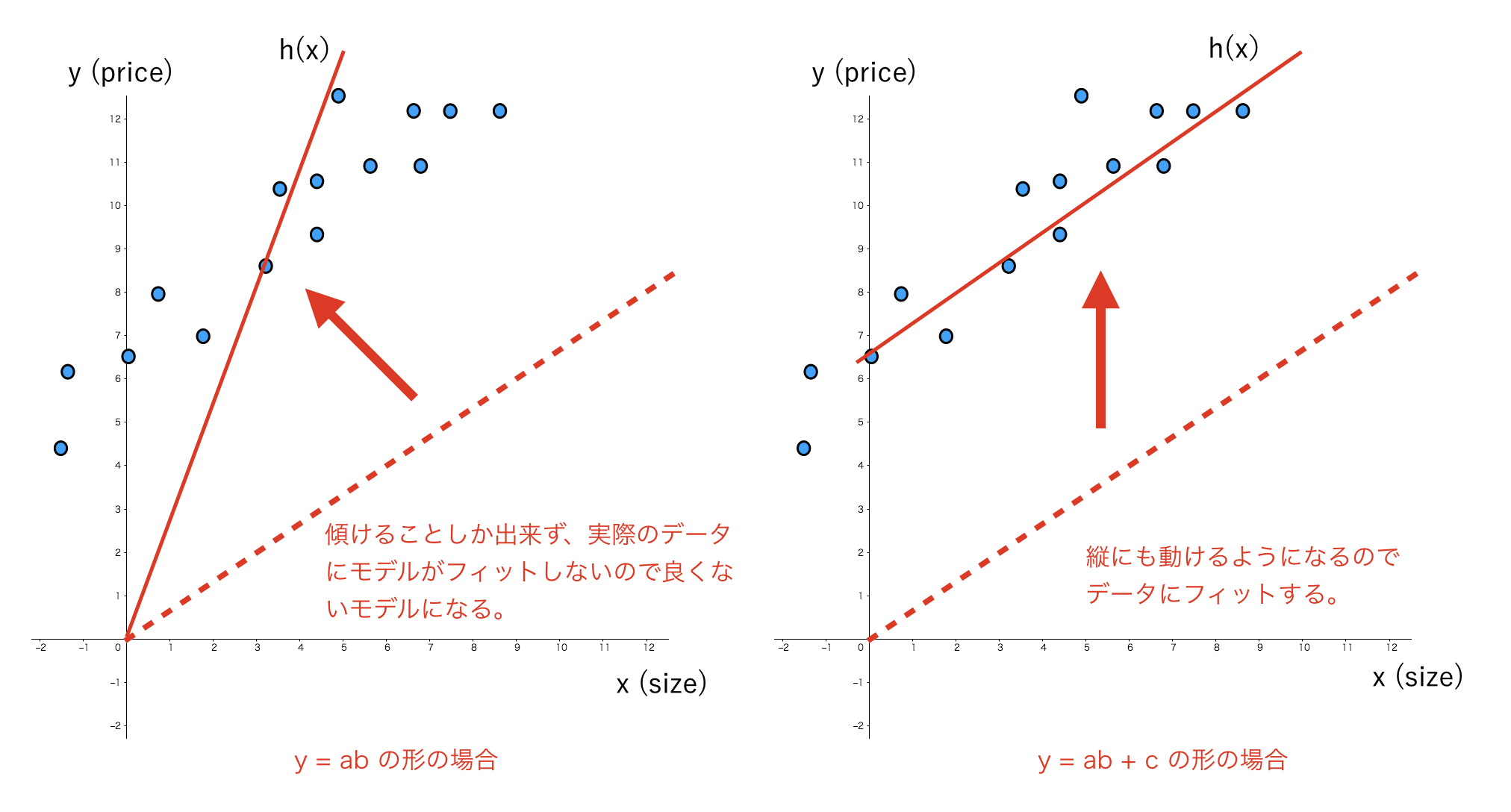
今回、特徴の数が「家の大きさ」の一つだけなので、y = ab + cと同じような式になります(Xoは式を同じような形にする目的で付けられており、実際に値はXo = 1となっており影響を与えないので分かりやすさのため一旦記述していません)
abで「どのくらい線を傾けるか」が決まり、cで「どのくらい線を高くするか」が決まります。
何故cを入れる必要があるかは以下の図で示します。
もし、入力として特徴を三つ入れる場合、仮設関数は以下のようになります。
\begin{align}
\newline
h(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 \\
\newline
x_1 ・・・・・・・・・・ 家の大きさ \\
x_2 ・・・・・・・・・・ ベッドの数 \\
x_3 ・・・・・・・・・・・・ 築年数 \\
\newline
\end{align}
xは実際のデータです。
θは自動で調節される値で、今回に関して言えば初期値は0でも良い。
最急降下法
θの更新方法です。
\theta_j = \theta_j - a \frac{d}{d \theta_j}J(\theta_j)
一見複雑そうに見える式ですが、一旦分かりやすさのためより簡単な式に直してみます。
\theta = \theta - \frac{d}{d \theta}J(\theta)
学習率aと特徴の添字jを式から省きました。
\frac{d}{d \theta}J(\theta)
前述で説明したことを思い出してみてください。
これはJ(θ)をθで微分するという意味で、「接線の傾き」を求めるための式です。
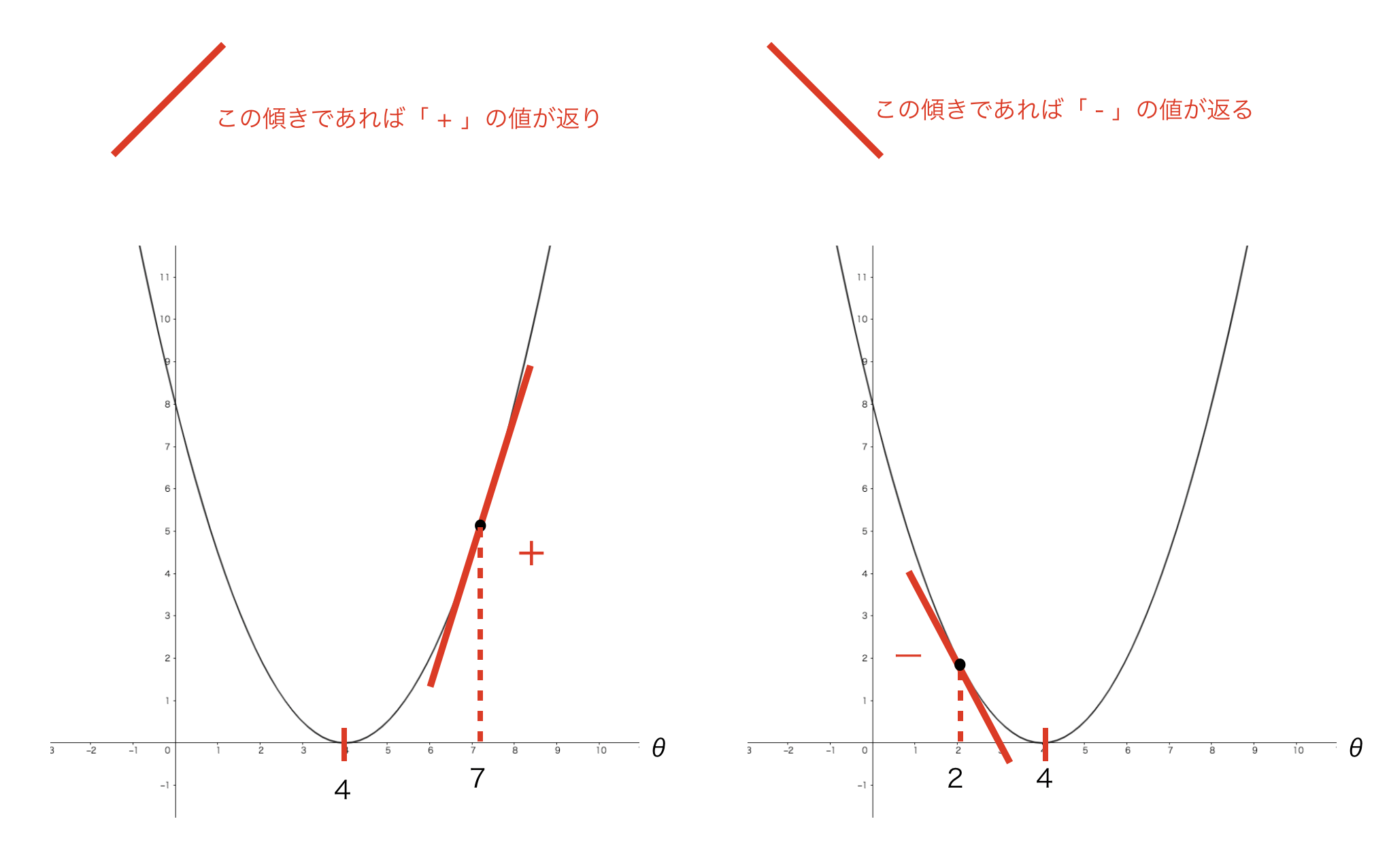
接線の傾きを何故求めているかというと、「傾き」がわかれば
「θを+に更新するべきか、-に更新するべきか方向が分かる」からです。
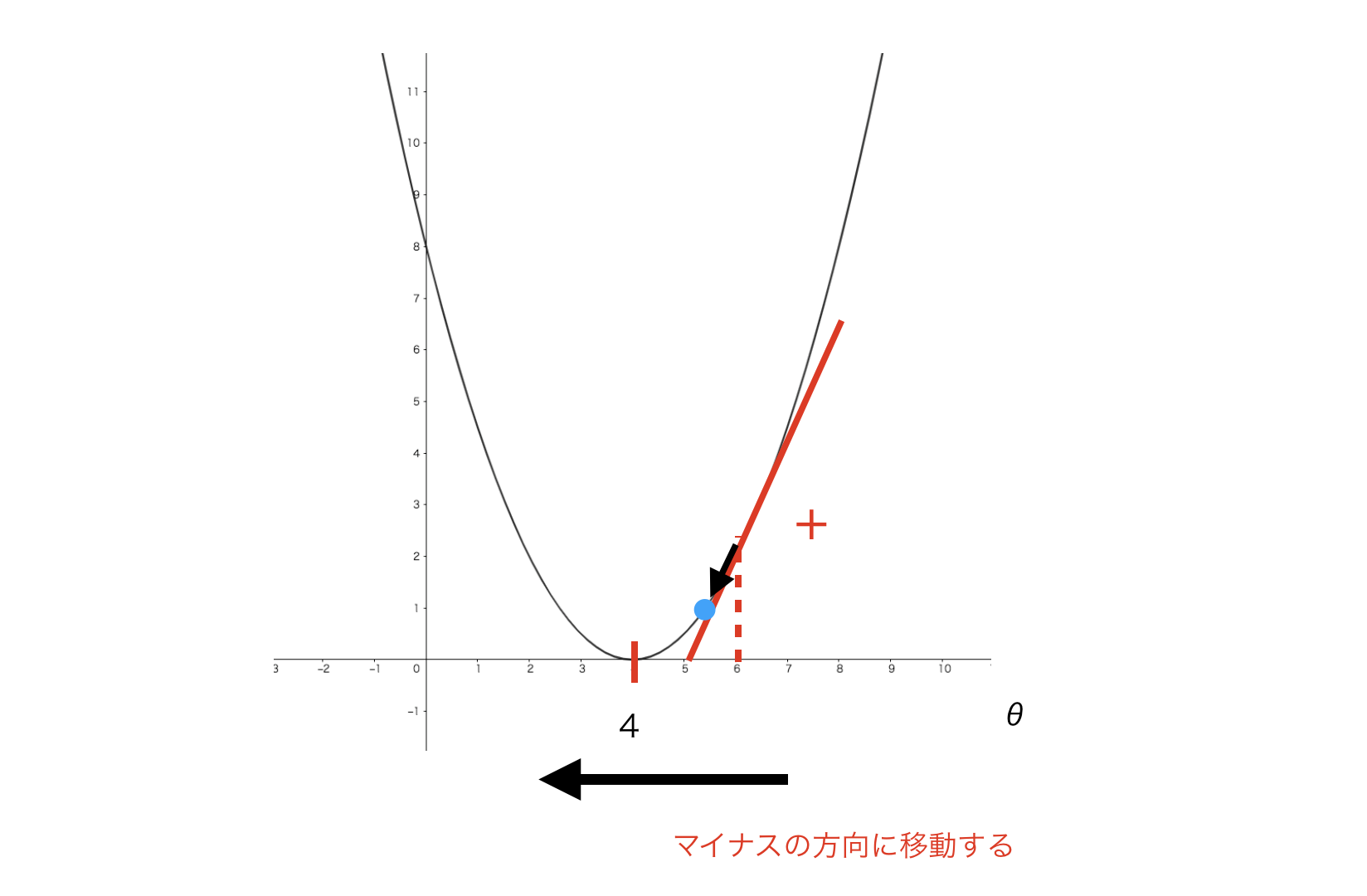
左図はθ = 7だった場合で、微分をすると+の値が返ってきます。
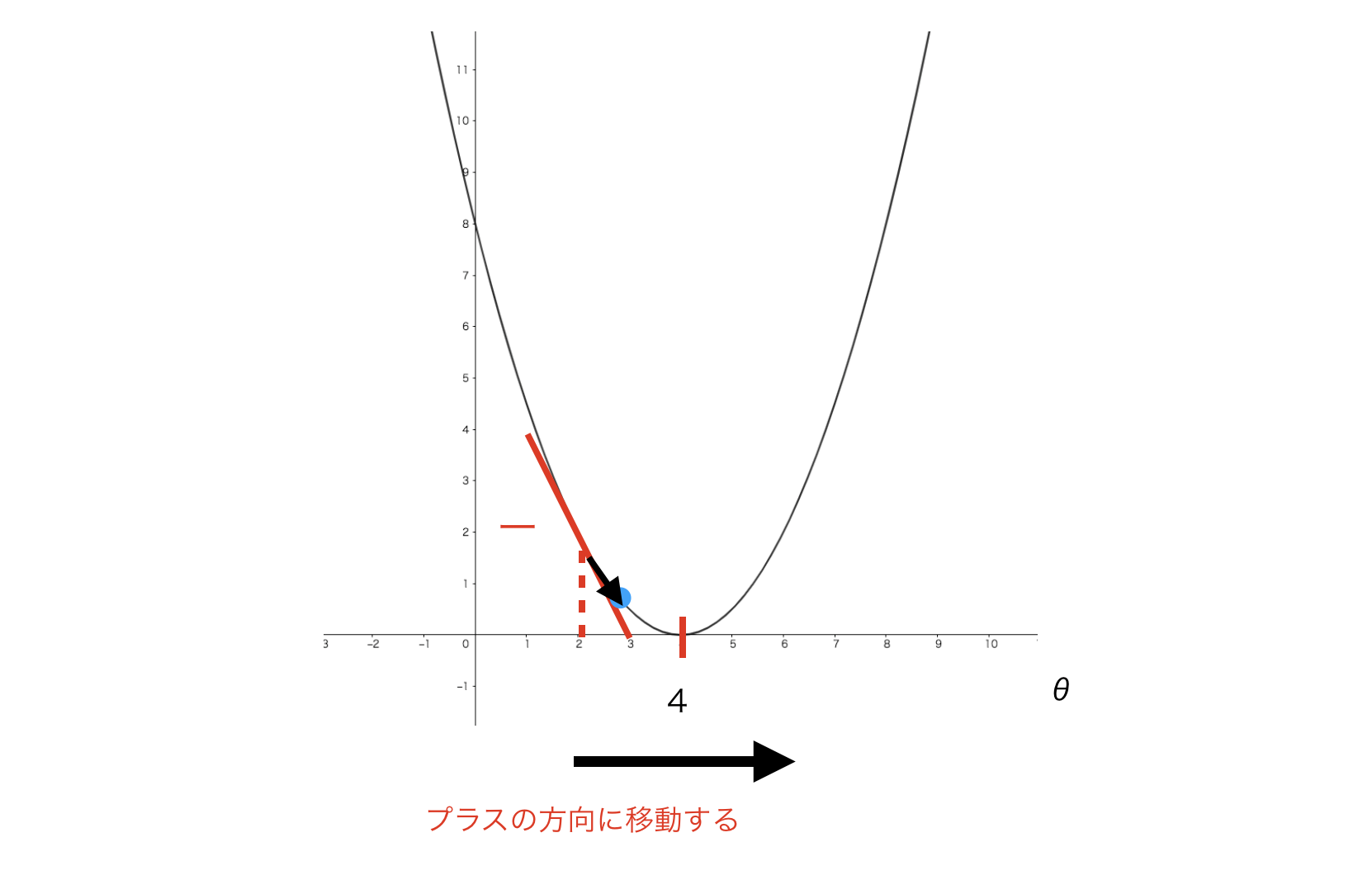
右図はθ = 2だった場合で、微分をすると-の値が返ってきます。
つまり、θ = 6だった場合、
\frac{d}{d \theta}J(\theta) = (+)の値
このようになり、
\theta = \theta - \frac{d}{d \theta}J(\theta)
これに(+)の値を代入すると
\theta = \theta -(+) \\
\theta = \theta * (ー)の値
となります。
つまり、「マイナス方向にθの値が更新」されることになります
逆もまた然り、今度はθ = 2の場合
\frac{d}{d \theta}J(\theta) = (-)の値
このようになり、
\theta = \theta - \frac{d}{d \theta}J(\theta)
これに(ー)の値を代入すると
\theta = \theta -(-) \\
\theta = \theta * (+)の値
となります。
つまり、「プラスの方向にθの値が更新」されることになります。
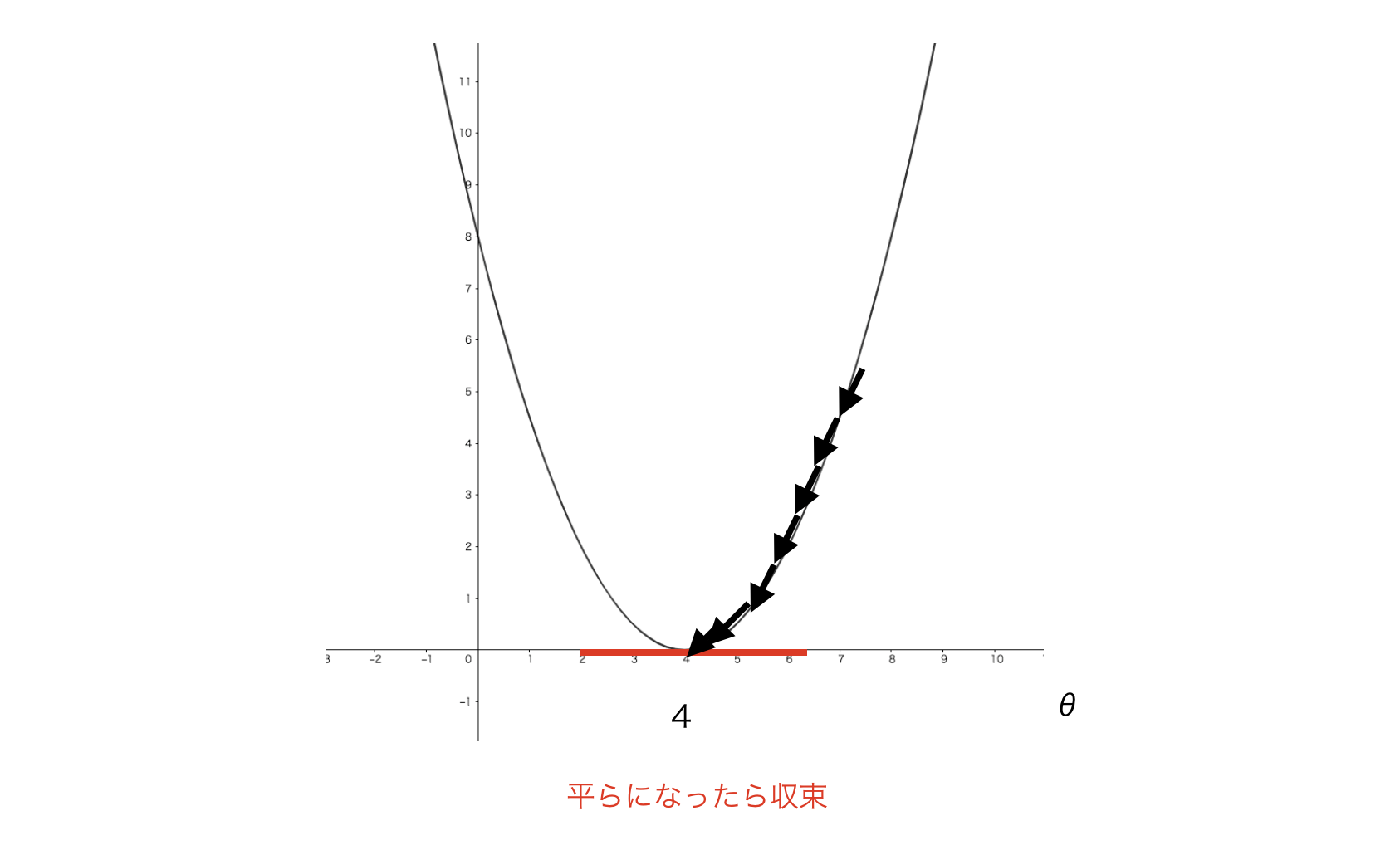
これを、収束するまで学習を繰り返します。
これで「家の値段を家の大きさで予測するモデル」が完成しました。
長くなってしまったため、ここまでとします(本当はSigmoid Functionあたりの話もするつもりでしたが)
ここまで読んでいただきありがとうございました。
GitHub
Perceptron
- Octaveで自作したコードで、機械学習学び始めの時に書いたコードなのであまり綺麗とは言えませんが参考までに。
NeuralNetwork
- こちらは個人的には自信作なので是非見てやって下さい m(_ _)m
次回
次回はニューラルネットワークについて説明します。