Juliaでブリルアンゾーン内の波数点を辿る （バンド図）

グラフェンのバンド図を描く際に、$\Gamma \to \text{K} \to \text{M} \to \Gamma$のように波数点を辿るわけですが、いかんせん波数メッシュを取るのが毎回面倒くさいです。

なので、生成AIのPerplexityくんに聞いてみました。

1回目

質問

グラフェンのブリルアンゾーンにおいて、Γ→K→M→Γの波数点を1000分割し、ブリルアンゾーンでの長さが等間隔になるようなJuliaのスクリプトを書いてください。

Answer

using Plots

# ブリルアンゾーンの頂点の座標
Γ = [0, 0]
K = [4π/(3a), 0]
M = [2π/a, 2π/(√3a)]

# 分割数
N = 1000

# Γ→K間の座標
kx_ΓK = range(Γ[1], stop=K[1], length=N÷3)
ky_ΓK = range(Γ[2], stop=K[2], length=N÷3)

# K→M間の座標
kx_KM = range(K[1], stop=M[1], length=N÷3)
ky_KM = range(K[2], stop=M[2], length=N÷3)

# M→Γ間の座標
kx_MΓ = range(M[1], stop=Γ[1], length=N÷3)
ky_MΓ = range(M[2], stop=Γ[2], length=N÷3)

# 座標の連結
kx = vcat(kx_ΓK, kx_KM, kx_MΓ)
ky = vcat(ky_ΓK, ky_KM, ky_MΓ)

# プロット
plot(kx, ky, aspect_ratio=:equal, legend=false)
scatter!([Γ[1], K[1], M[1]], [Γ[2], K[2], M[2]], color=:red, markersize=5)

このスクリプトでは、ブリルアンゾーンの頂点Γ、K、Mの座標を定義し、それぞれの間を1000分割した座標を生成しています。Γ→K、K→M、M→Γの順に座標を連結し、最終的にkxとkyの配列を得ています。

最後にプロットを行い、ブリルアンゾーンの形状と頂点の位置を可視化しています。aspect_ratio=:equalオプションにより、x軸とy軸の比率を等しくすることで、ブリルアンゾーンの正六角形の形状が保たれます。[1]

Citations:
[1] https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/269379/1/bussei_el_101209.pdf
[2] https://core.ac.uk/download/pdf/235956767.pdf
[3] https://flex.phys.tohoku.ac.jp/riron/ronbun/m14mizu.pdf
[4] http://maya.phys.kyushu-u.ac.jp/~knomura/education/Undergraduate/Busseibutsuri-II/Condensed-Matter-II.pdf
[5] https://home.hiroshima-u.ac.jp/ino/lecture/SSP1note8_ino2017.pdf

---

...悪くないですねぇ。けど、経路にかかわらず一定の刻み数にしてしまっているので、少しいけ好かないです。

2回目

質問

各セグメントの長さが異なるため、単純に等分割するのではなく、セグメントの長さに応じて分割数を調整してください。

Answer

各セグメントの長さに応じて分割数を調整するために、以下のように修正したスクリプトを提案します。

using Plots

# ブリルアンゾーンの頂点の座標
Γ = [0, 0]
K = [4π/(3a), 0]
M = [2π/a, 2π/(√3a)]

# 総分割数
N = 1000

# セグメントの長さを計算
ΓK = sqrt((K[1]-Γ[1])^2 + (K[2]-Γ[2])^2)
KM = sqrt((M[1]-K[1])^2 + (M[2]-K[2])^2)
MΓ = sqrt((Γ[1]-M[1])^2 + (Γ[2]-M[2])^2)
total_length = ΓK + KM + MΓ

# セグメント毎の分割数を計算
nΓK = round(Int, N * ΓK / total_length)
nKM = round(Int, N * KM / total_length)
nMΓ = N - nΓK - nKM

# Γ→K間の座標
kx_ΓK = range(Γ[1], stop=K[1], length=nΓK)
ky_ΓK = range(Γ[2], stop=K[2], length=nΓK)

# K→M間の座標
kx_KM = range(K[1], stop=M[1], length=nKM)
ky_KM = range(K[2], stop=M[2], length=nKM)

# M→Γ間の座標
kx_MΓ = range(M[1], stop=Γ[1], length=nMΓ)
ky_MΓ = range(M[2], stop=Γ[2], length=nMΓ)

# 座標の連結
kx = vcat(kx_ΓK, kx_KM, kx_MΓ)
ky = vcat(ky_ΓK, ky_KM, ky_MΓ)

# プロット
plot(kx, ky, aspect_ratio=:equal, legend=false)
scatter!([Γ[1], K[1], M[1]], [Γ[2], K[2], M[2]], color=:red, markersize=5)

主な変更点は以下の通りです。

1. セグメントの長さを計算する部分を追加しました。
2. 総分割数Nを1000に固定し、各セグメントの分割数をセグメントの長さに応じて計算しています。
3. range関数の長さをセグメント毎の分割数に合わせて変更しています。

これにより、各セグメントの長さに応じて分割数が調整され、ブリルアンゾーンの形状がより正確に表現されるようになります。

---

おお！求めていた方法を教えてくれました！

3回目

質問

あなたが最終的に提示したJuliaスクリプトが一度で取得できるような質問文を教えてください。

Answer

以下のような質問文で、最終的に提示したJuliaスクリプトが一度で取得できます。

グラフェンのブリルアンゾーンにおいて、Γ→K→M→Γの波数点を1000分割し、セグメントの長さに応じて分割数を調整し、ブリルアンゾーンでの長さが等間隔になるようなJuliaのスクリプトを書いてください。ただし、ブリルアンゾーンの頂点Γ、K、Mの座標は以下の通りとします。

Γ =
K = [4π/(3a), 0]
M = [2π/a, 2π/(√3a)]

また、最終的なプロットでは、ブリルアンゾーンの形状と頂点の位置を可視化してください。

---

だそうです。

最終版

ということで、これらのコードを参考に、一般の経路で使えるようなJuliaスクリプトを書きました。

function make_k(
    k_point::Dict,
    k_point_list::Array,
    N_k::Int64
    )::Tuple{Matrix{Float64},Vector{Int64}}

    # Γ, K, M 点の座標
    k_data = [k_point[k] for k ∈ k_point_list]

    # Γ->K, K->M, M->Γ 間の距離
    d_list = [norm(k) for k ∈ (circshift(k_data,-1) - k_data)]

    # k 点の数
    points = [round(Int, N_k * d / sum(d_list)) for d ∈ d_list]

    n_points = [0]
    for i ∈ points
        push!(n_points,n_points[end]+i)
    end

    kpoints = reduce(hcat,
        [
            reduce(hcat,[(1-t)*k_data[i] + t*circshift(k_data,-1)[i] for t ∈ range(0,1,points[i]) ]) for i ∈ 1:length(k_point_list)-1
        ])

    return kpoints, n_points
    
end

function make_k(k_point, k_point_list)
    N_k = length(k_point_list)*64
    make_k(k_point,k_point_list,N_k)
end

こんな感じで使います。

    k_point = Dict(
        :Γ => [0, 0],
        :K => [2π/3, 2π/√3],
        :M => [0, 2π/(√3)],
    )
    k_point_list = [:Γ, :K, :M, :Γ,]

    kpoints, npoints = make_k(k_point,k_point_list,1000)
    band = hcat(
        [eigvals(Hamiltonian(kx,ky)) for (kx,ky) in eachcol(kpoints)]...
        )

    plot(band', xticks=(npoints,k_point_list))

試してみよう

それこそ、グラフェンで書いてみましょう。面倒くさいので再びPerplexityくんの登場

4回目

質問

2次元グラフェンのタイトバインディング模型におけるハミルトニアンを取得する関数をJuliaスクリプトで作成してください。

Answer

以下は、2次元グラフェンのタイトバインディング模型におけるハミルトニアンを取得する関数をJuliaで実装したスクリプトです。

using LinearAlgebra

function graphene_hamiltonian(kx, ky, t=1.0)
    a = 1.42 # グラフェンの格子定数[Å]
    
    # 波数ベクトルをパラメータとするハミルトニアンの行列要素を計算
    f = kx * a + 1im * ky * a
    H11 = 0
    H12 = t * (1 + 2 * cos(ky * a * √3/2) * exp(1im * kx * a / 2))
    
    # ハミルトニアンの行列を構築
    H = [H11  H12;
         conj(H12) H11]
    
    return H
end

このスクリプトでは、以下の手順でグラフェンのタイトバインディング模型のハミルトニアンを計算しています。

1. グラフェンの格子定数aを定義します。[1]
2. 波数ベクトル(kx, ky)に依存する行列要素H11とH12を計算します。[3]
   • H11は対角要素で0になります。
   • H12は非対角要素で、ホッピングエネルギーtと波数ベクトルの関数で表されます。
3. ハミルトニアンの行列Hを構築します。
   • H11とH12を用いて2x2の行列Hを作成します。
   • H12の共役複素数conj(H12)を対角要素に設定することで、ハミルトニアンが自己共役になります。
4. 計算したハミルトニアンの行列Hを返します。

この関数を用いることで、任意の波数ベクトル(kx, ky)におけるグラフェンのタイトバインディング模型のハミルトニアンを簡単に取得できます。

Citations:
[1] https://patricia.ph.tsukuba.ac.jp/~hatsugai/files/PDF/from-rhodia/hatsugai_gra.pdf
[2] http://maya.phys.kyushu-u.ac.jp/~knomura/education/Undergraduate/Busseibutsuri-II/Condensed-Matter-II.pdf
[3] http://cms.phys.s.u-tokyo.ac.jp/pdf/HatsugaiAoki.pdf
[4] https://www.jstage.jst.go.jp/article/butsuri/72/12/72_872/_pdf/-char/ja
[5] https://home.hiroshima-u.ac.jp/ino/lecture/SSP1note8_ino2017.pdf

---

ということで、果たしでできるでしょうか...？

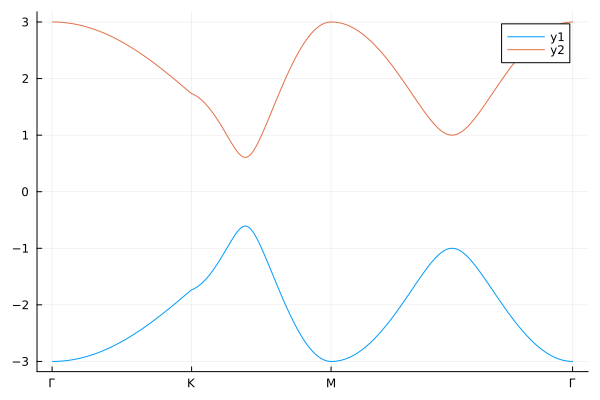
...Diracコーンが消え失せました！！！
まだまだ質問の改良の余地ありですね（笑）

最後に

いつもいい感じに作っても忘れてしまうので、備忘録を残しました。
Perplexityくん、今後ともよろしくね。