センター数学2B（2018年）をpythonで解いてみた

• 実行環境
• Cent6.9
• python3.6.5
• VirtualBox 5.2.2
• 問題は参考書または、インターネットを参照ください。

第1問

(1)

加法定理や三角関数の合成はπが数字になる、分数が計算されてしまうなどで
少し無理やりな求め方になりました。

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math

x = symbols('x')
# シータの代わり
a = symbols('a')
# パイの代わり
b = symbols('b')
sin = symbols('sin')
cos = symbols('cos')

deg = math.degrees(1)
if deg == 360/math.pi:
    print("0")
elif deg == 360/(math.pi**3):
    print("1")
elif deg == 180/math.pi:
    print("2")
elif deg == 180/(math.pi**3):
    print("2")

print(math.radians(144)/math.pi)
print(math.degrees(23/12*math.pi))

f = 2*sin*(a+b/5) - 2*cos(a+b/30) -1
diff = (a+b/30) - (a+b/5)
g = f.subs(a+b/5, x).subs(a+b/30, x + diff)
print(g)
h = g.subs(cos(x+diff), (cos*x*math.cos(diff.subs(b, math.pi))-sin*x*math.sin(diff.subs(b, math.pi))))
print(h)
c = h.coeff(sin*x, 1)
d = h.coeff(cos*x, 1)
e = round(c/(math.sqrt(c**2+d**2)), 2)
f = round(d/(math.sqrt(c**2+d**2)), 2)

radList = (-5*b/6, -3*b/4, -2*b/3, -1*b/2, -b/3, -b/4, -b/6, 0*b, b/6, b/4, b/3, b/2, 2*b/3, 3*b/4, 5*b/6, 1*b)
num = 0
for radian in radList:
    if e == round(math.cos(radian.subs(b, math.pi)),2) and f == round(math.sin(radian.subs(b, math.pi)),2):
        num = radian
        print("ケ:", radian)

i = round(1/sqrt(c**2+d**2), 2)
print("コ", i)
radList = (-5*b/6, -3*b/4, -2*b/3, -1*b/2, -b/3, -b/4, -b/6, 0*b, b/6, b/4, b/3, b/2, 2*b/3, 3*b/4, 5*b/6, 1*b)
for radian in radList:
    if i == round(math.sin(radian.subs(b, math.pi)),2) and ((radian-num-b/5).subs(b, math.pi) >= math.pi/2) and ((radian-num-b/5).subs(b, math.pi) <= math.pi):
        print(radian-num-b/5)

出力

2
0.8
345.0
2*sin*x - 2*cos(-b/6 + x) - 1
-1.73205080756888*cos*x + 1.0*sin*x - 1
ケ: -b/3
コ 0.5
29*b/30

解答
ア:2、イ:4、ウ:5、エ:3、オ:4、
カ:5、キ:6、ク:3、ケ:3、コ:2
サ:2、シ:9、ス:3、セ:0

##(2)
プログラム
sympy.logだと値が出力されなかったため、
sympy.logとmath.logを使い分けてでしか解けなかったので、
プログラムとしては汚くなっています。

# -*- coding: utf-8 -*-

from sympy import *
import math
from sympy.solvers.inequalities import *

x = symbols('x')
c = symbols('c')
t = symbols('t')

f = x**log(x, 3)
g = (x/c)**3
ff = log(x, 3)**2
gg = 3*log(x, 3) - 3*log(c, 3)
print((ff-gg).subs(log(x, 3), t))
h = (ff-gg).subs(log(x, 3), t).subs(c, 9**(1/3)).subs(log(3), math.log(3))
domain = Interval(0, S.Infinity)
print(reduce_rational_inequalities([[h >= 0]], t))

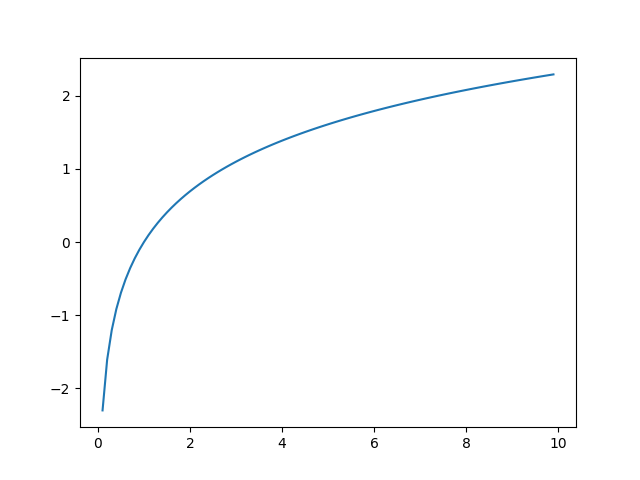
x_value = np.arange(0.1, 10, 0.1)
y_value = np.log(x_value)
plt.plot(x_value, y_value)
plt.show()
plt.savefig('1-2.png')

n = solve(diff((ff-gg).subs(log(x, 3), t), t), t)[0]
m = log(c, 3) - (ff-gg).subs(log(x, 3), t).subs(t, n)/3
print(m)
print(3**m)

出力

t**2 - 3*t + 3*log(c)/log(3)
((2.0 <= t) & (t < inf)) | ((t <= 1.0) & (-inf < t))
3/4
3**(3/4)

解答
ソ:2、タ:3、チ:1、ツ:2、テ:0、ト:3
ナ:9、ニ:2、ヌ:3、ネ:4、ノ:4、ハ:2、ヒ:7

第2問

(1)

グラフを作成するのに別プログラムを用いてしまったのが、
個人的に悔しいです。

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math
import numpy as np

x = symbols('x')
p = symbols('p')
q = symbols('q')
r = symbols('r')
v = symbols('v')

f = p*x**2+q*x+r
g = 2*x-1

q_value = solve((diff(f, x)-2).subs(x, 1), q)[0]
print("q =", q_value)
r_value = solve(f.subs(x, 1).subs(q, q_value)-1, r)[0]
print("r =", r_value)

ff = f.subs(q, q_value).subs(r, r_value)
s = integrate(ff-g, (x, 1 ,v)).expand()
print("S =", s)
t = integrate(g, (x, 1, v))
print("T =", t)
p_value = solve(diff(s-t, v).subs(v, 2), p)[0]
print("p =", p_value)
v_0_list = solve((s-t).subs(p, p_value), v)
v_0 = 0
for tmp_v_0 in v_0_list :
    if tmp_v_0 > 1 :
        v_0 = tmp_v_0
        break
print("v0 =", v_0)
u = (s-t).subs(p, p_value)
print(u)
min_p = 0
tmp_min = 0
min = 0
flag = 0
for tmp_min_v in solve(diff(u, v), v) :
    if tmp_min_v >= 1 :
        if flag==0 :
            min = u.subs(v, tmp_min_v)
            flag = 1
        tmp_min = u.subs(v, tmp_min_v)
        if tmp_min <= min :
            mim = tmp_min
print(min)

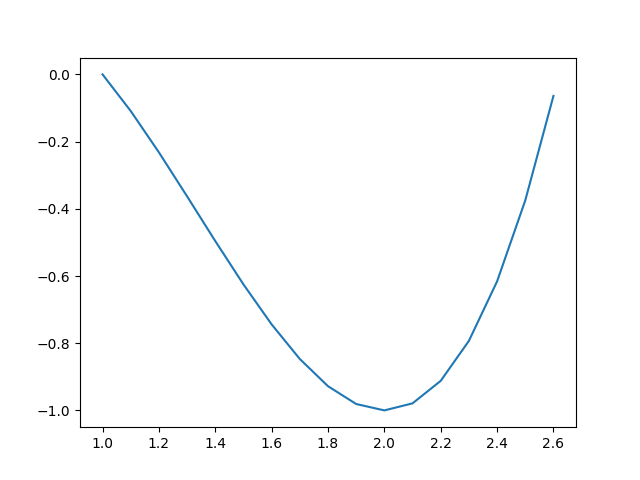
ソの確認

import matplotlib.pyplot as plt
import numpy as np
import math

x = np.arange(1, math.sqrt(5)/2 + 3/2, 0.1)
y = x**3 - 4*x**2 + 4*x - 1
plt.plot(x, y)
plt.show()
plt.savefig('2-1.png')

出力

q = -2*p + 2
r = p - 1
S = p*v**3/3 - p*v**2 + p*v - p/3
T = v**2 - v
p = 3
v0 = sqrt(5)/2 + 3/2
v**3 - 4*v**2 + 4*v - 1
-1

解答
ア:2、イ:-、ウ:2、エ:2、オ:1
カ:3、キ:3、ク:3、ケ:1、コ:2
サ:3、シ:3、ス:5、セ:2、ソ:3
タ:-、チ:1

(2)

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math
import numpy as np

t = symbols('t')
height = sqrt(((t**2+1)**2 - ((2*t**2-2)/2)**2).expand())
w = -1 * (((2*t**2-2)*height)/2).expand()
print(diff(w, t))

出力

-6*t*sqrt(t**2) + 2*sqrt(t**2)/t

解答
ツ:7、テ:4、ト:-、ナ:6、ニ:2、ヌ:2

第3問

数列の総和を求めるのが難しいです。
どうしても一般項を見てからプログラムを追加する方法になってしまいます。

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math
import numpy as np

a1 = symbols('a1')
n = symbols('n')
r = symbols('r')

f = 0
g = 0
for num in range(0, 8) :
    if num == 3 :
        f += 30
    else :
        f += a1 + num*n

    if num >= 3 :
        g += 30 + (num-3)*n
    else :
        g += a1 + num*n

diffFirstTerm = solve([f-288, g-288], [a1, n]).get(a1)
commonDiff = solve([f-288, g-288], [a1, n]).get(n)
print("初項:", diffFirstTerm)
print("公差:", commonDiff)
Sn = (1/2*n*(2*diffFirstTerm+(n-1)*commonDiff)).expand()
print("Sn =", Sn)

f = 0
g = 0
for num in range(0, 3) :
    if num == 1 :
        f += 36
    else :
        f += a1*(r**num)

    if num >= 1 :
        g += 36*(r**(num-1))
    else :
        g += a1*(r**num)

ratioFirstTerm = 0
commonRatio = 0
for item in solve([f-156, g-156], [a1, r]) :
    if item[1] > 1 :
        ratioFirstTerm = item[0]
        commonRatio = item[1]
print("初項:", ratioFirstTerm)
print("公比:", commonRatio)
Tn = (ratioFirstTerm*(1-commonRatio**n))/(1-commonRatio)
print("Tn =", Tn.factor())

dn = (Sn.subs(n, n+1) - Tn.subs(n, n+1)).expand()
print("dn =", dn)
c1 = diffFirstTerm - ratioFirstTerm
print("c1 =", c1)
# ここだけdnを見てから無理やり
cn = c1 + dn.subs(n**2, 1/6*n*(n-1)*(2*n-1)).subs(3**n, (3*(1-3**(n-1)))/(1-3))
print(cn.expand())

出力

初項: -6
公差: 12
Sn = 6.0*n**2 - 12.0*n
初項: 12
公比: 3
Tn = 6*(3**n - 1)
dn = -18*3**n + 6.0*n**2
c1 = -18
-9*3**n + 2.0*n**3 - 3.0*n**2 + 1.0*n + 9

解答
ア:-、イ:6、ウ:1、エ:2、オ:6
カ:1、キ:2、ク:1、ケ:2、コ:3
サ:6、シ:3、ス:1、セ:5、ソ:6
タ:3、チ:2、ツ:-、テ:1、ト:8
ナ:2、ニ:3、ヌ:9、ネ:2

第4問

一部だけ展開させる方法が分からないので、
すべて展開させる形になっているのが残念です。

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math
import numpy as np

a = symbols('a')
p = symbols('p')
q = symbols('q')
r = symbols('r')
s = symbols('s')
t = symbols('t')

ab = q-p
print("ab^2 =", (ab**2).expand())
fd = p+1/4*(q-p)
print("fd =", fd)
f = solve(fd-s*r, q)[0]
print("q =", f)
bc = r-q
fe = q+ a*(r-q)
g = solve(fe-t*p, q)[0].expand()
print("q =", g)
p_coef_f = f.coeff(p, 1)
r_coef_f = f.coeff(r, 1)
p_coef_g = g.coeff(p, 1)
r_coef_g = g.coeff(r, 1)
s_value = solve(r_coef_f-r_coef_g, s)[0]
t_value = solve(p_coef_f-p_coef_g, t)[0]
print("s =", s_value)
print("t =", t_value)
be = t_value*p-q
print("be^2 =", (be**2).expand().subs(p**2, 1))
print("p*q =", solve((ab**2).expand().subs(p**2, 1)-(be**2).expand().subs(p**2, 1), p*q))

出力

ab^2 = p**2 - 2*p*q + q**2
fd = 0.75*p + 0.25*q
q = -3.0*p + 4.0*r*s
q = a*r/(a - 1) - p*t/(a - 1)
s = 0.25*a/(a - 1.0)
t = 3.0*a - 3.0
be^2 = 9.0*a**2 - 6.0*a*p*q - 18.0*a + 6.0*p*q + q**2 + 9.0
p*q = [1.5*a - 1.0]

解答
ア:2、イ:2、ウ:3、エ:4、オ:1
カ:4、キ:-、ク:3、ケ:4、コ:1
サ:a、シ:a、ス:-、セ:a、ソ:4
タ:-、チ:3、ツ:9、テ:6、ト:3
ナ:a、ニ:2、ヌ:2

第5問

正規分布表をすべて打ち込むのが面倒だったので、
そこだけ値をプログラムに入れました。

プログラム

# -*- coding: utf-8 -*-

from sympy import *
import math
import numpy as np
from statistics import mean, pvariance

def getConfidenceInterval(r, z, n) :
    return (r+z*math.sqrt((r*(1-r))/n)) - (r-z*math.sqrt((r*(1-r))/n))


a = symbols('a')
s = symbols('s')
t = symbols('t')
X = symbols('X')

P_X_2a = 1/a
print("P(X=2a) =", P_X_2a)

numList = []
for num in range(1, 6) :
    numList.append(2*num)

print("ウ:", mean(numList))
print("エ:", pvariance(numList))

f = (s*X+t).subs(X, mean(numList))
g = (s**2*X).subs(X, pvariance(numList))
s_value = 0
t_value = 0
for answerList in solve([f-20, g-32], [s, t]) :
    if answerList[0] > 0 :
        s_value = answerList[0]
        t_value = answerList[1]

print("s =", s_value)
print("t =", t_value)

cnt = 0
for num in numList :
    if (s_value*X+t_value).subs(X, num) >= 20 :
        cnt += 1

print(Rational(cnt, numList.__len__()))

P_A = (a*(a-1)*(a-2))/(3*2*1)/(a*(a-1)*(a-2))
print("P(A) =", P_A)
# 二項分布
A_mean = 180*P_A
A_variance = 180*P_A*(1-P_A)
print("コサ:", A_mean)
print("シス:", A_variance)
print("セソタ:", (18-A_mean)/math.sqrt(A_variance))
print("チツテ:", (36-A_mean)/math.sqrt(A_variance))
# 正規分布表から取得
print("トナ:", round(0.4918+0.3849, 2))

ratio = 320/400
print("ニ:", ratio)
print("ヌネ:", round(ratio-1.96*math.sqrt((ratio*(1-ratio))/400), 2))
print("ノハ:", round(ratio+1.96*math.sqrt((ratio*(1-ratio))/400), 2))
L1 = getConfidenceInterval(ratio, 1, 400)
L2 = getConfidenceInterval(0.6, 1, 400)
L3 = getConfidenceInterval(0.8, 1, 500)
list = {"L1" : L1,
        "L2" : L2,
        "L3" : L3}
sortList = sorted(list.items(), key=lambda x:x[1])
print(sortList)

出力

P(X=2a) = 1/a
ウ: 6
エ: 8
s = 2
t = 8
3/5
P(A) = 1/6
コサ: 30
シス: 25
セソタ: -2.40000000000000
チツテ: 1.20000000000000
トナ: 0.88
ニ: 0.8
ヌネ: 0.76
ノハ: 0.84
[('L3', 0.03577708763999654), ('L1', 0.040000000000000036), ('L2', 0.04898979485566346)]

解答
ア:1、イ:a、ウ:6、エ:8、オ:2
カ:8、キ:6、ク:1、ケ:6、コ:3
サ:0、シ:2、ス:5、セ:2、ソ:4
タ:0、チ:1、ツ:2、テ:0、ト:8
ナ:8、ニ:8、ヌ:7、ネ:6、ノ:8
ハ:4、ヒ:4