加法性白色ガウス雑音環境下におけるBPSKシミュレーション

概要

伝搬路で白色ガウス雑音が付加されるパスバンドモデル．SNRに対するBERを求める．

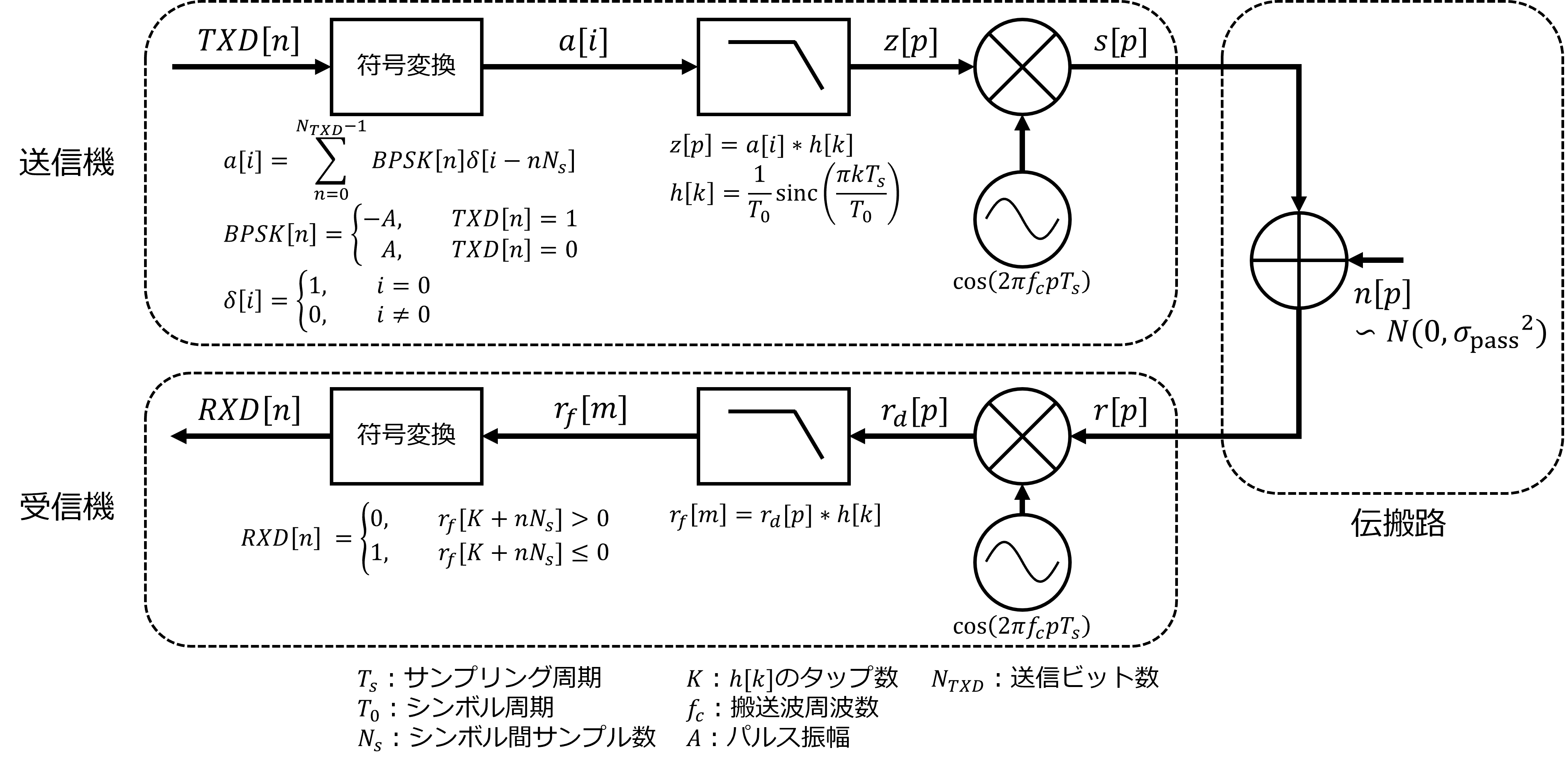
システムモデル

受信側シンボル判定（符号変換）時のSNR

$n[p] = 0$としてシンボル判定時の信号電力を計算する．
まず，ダウンコンバートした後の信号$r_d[p]$を式変形すると次のようになる．

\begin{align}
r_d[p] &= (a[i] \ast h[k])\cos^2(2\pi f_cpT_s)\\
&= (a[i] \ast h[k])\left[ \frac{1}{2} \left( 1 + \cos(4\pi f_cpT_s) \right) \right]
\end{align}

受信側のLPFによって$\cos(4\pi f_cpT_s)$の項は消えるため，LPFの出力信号$r_f[m]$は

\begin{align}
r_f[m] &= r_d[p] \ast h[k]\\
&= \frac{1}{2} a[i] \ast h[k] \ast h[k]
\end{align}

となる．これはインパルス列$a[i]$と$h[k] \ast h[k]$の畳み込みである．$h[k] \ast h[k]$の最大値を求めると

\max \left( h[k] \ast h[k] \right) = \sum_{k=-K/2}^{K/2} h[k]^2

となり，シンボル判定時の振幅は

\frac{1}{2}A\sum_{k=-K/2}^{K/2} h[k]^2

となる．よってシンボル判定時の信号電力は

P_s = \frac{A^2}{4} \left( \sum_{k=-K/2}^{K/2} h[k]^2 \right)^2

同様に，$s[p]=0$として雑音電力を計算する．
$r_d[p]$の分散を計算すると，

\begin{align}
V\left[r_d[p]\right]&=V\left[n[p]\cos(2\pi f_cpT_s)\right]\\
\end{align}

ここで$n[p]$も$\cos(2\pi f_cpT_s)$も平均は0なので，

\begin{align}
&=E\left[\left( n[p]\cos(2\pi f_cpT_s)  \right)^2\right]\\
&= E\left[ n[p]^2 \right] E\left[ \cos^2(2\pi f_cpT_s)\right]\\
&= \frac{1}{2} {\sigma_\mathrm{pass}}^2
\end{align}

また，一般に，$h[k]$と分散$\sigma$の独立無相関な信号$n[j]$の畳み込みの分散は

\sigma^2 \sum h[k]^2

となる．

よってシンボル判定時の雑音電力は

\sigma^2 = \frac{{\sigma_\mathrm{pass}}^2}{2} \sum_{k=-K/2}^{K/2}h[k]^2

したがってシンボル判定時のSNRは次のようになる．

SNR = \frac{P_s}{\sigma^2} = \frac{A^2 \sum_{k=-K/2}^{K/2}h[k]^2}{2 {\sigma_\mathrm{pass}}^2}

ソースコード

clear;

%データレートよりもサンプリング周波数の方が十分大きくなければならない
%データレート<搬送波周波数<サンプリング周波数である必要がある
Fs = 100;                                   %サンプリング周波数[Hz]
Ts = 1/Fs;                                  %サンプリング周期[s]
Ns = 5;                                     %シンボル間サンプル数
T0 = Ns*Ts;                                 %シンボルの周期（ナイキスト周期）[s]
Fc = 20;                                    %搬送波周波数[Hz]
A  = 1;                                     %振幅[V]
TXD_N = 1e4;                                %ランダム生成するビット数[bit]
TXD = logical(randi([0, 1], [1, TXD_N]));   %送信ビット列(ランダム)
t  = 0:Ts:(numel(TXD)-1)*T0;                %離散時間[s]

%信号空間ダイアグラムへのマッピング
BPSK(TXD==0) =  A;
BPSK(TXD==1) = -A;

%インパルス列作成
a = zeros(1,numel(t));
a(1:Ns:end) = BPSK;

%フィルタのインパルス応答を計算
k  = 500;                %フィルタインパルス応答の打ち切り時間調整
tf = -T0*k:Ts:T0*k-Ts;   %フィルタインパルス応答の時間列
h  = (1/T0).*sinc(tf/T0);
h  = h./norm(h);

%インパルス列をフィルタに通過させる
z = conv(a,h);              %畳み込み

t_1 = 0:Ts:(numel(z)-1)*Ts; %フィルタ通過後の離散時間

%ベースバンド信号を搬送波に乗せる
carrier = cos(2*pi*Fc*t_1);   %搬送波

%変調波
s = z.*carrier;

%雑音電力を変えてシミュレーション
SNR_dB_sim = 0:12;
BER_sim = zeros(1,numel(SNR_dB_sim));
for index = 1:numel(SNR_dB_sim)
    %雑音生成
    noisePower_pass = A^2*sumsqr(h)/(2*db2pow(SNR_dB_sim(index)));
    n = wgn(1,numel(s),noisePower_pass ,'linear',1,1);

    %受信信号
    r = s + n;

    %同期検波
    rd = r.*carrier; %受信波と基準信号と掛ける

    %高調波を除去
    %rdをフィルタに通過させる
    rf_1 = conv(rd,h);                         %畳み込み
    rf_2 = rf_1(numel(h)+1:numel(h)+numel(t)); %遅延補正
    
    %ビット判定（符号変換）
    RXD = zeros(1,numel(TXD));
    RXD(rf_2(a ~= 0)> 0) = 0;
    RXD(rf_2(a ~= 0)<=0) = 1;

    BER_sim(index) = sum(RXD~=TXD)./numel(TXD);
end

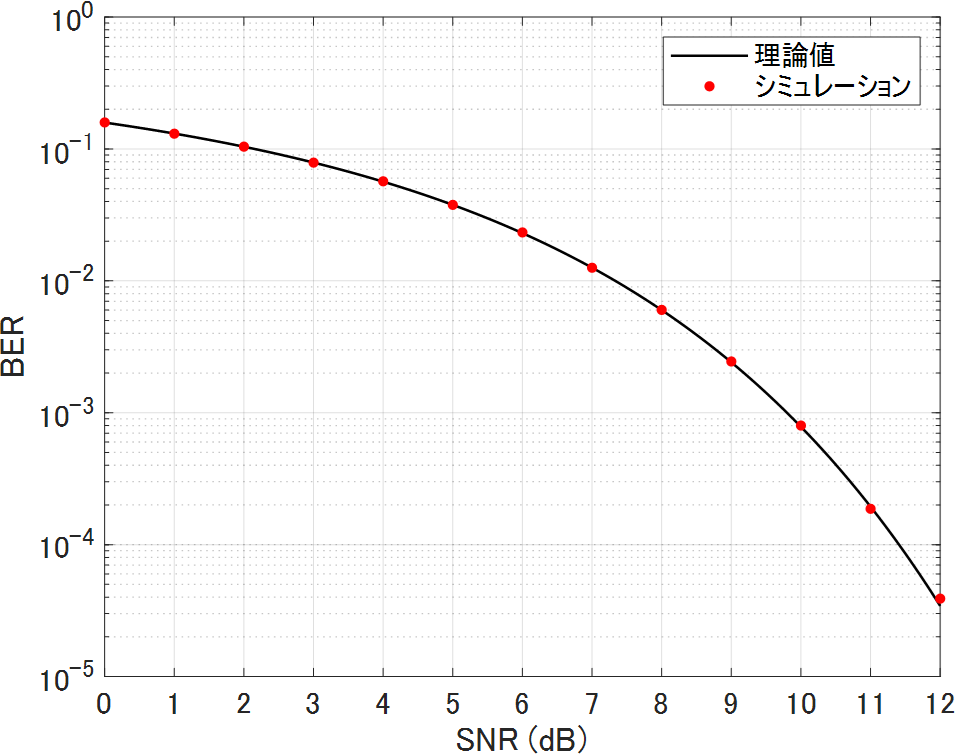
SNR_dB_theory = linspace(0,12,1000);
BER_theory = 1/2.*erfc(sqrt(db2pow(SNR_dB_theory)./2));

semilogy(SNR_dB_theory,BER_theory,SNR_dB_sim,BER_sim,".");
xticks(0:SNR_dB_sim(end));
grid on
xlabel('SNR (dB)');
ylabel('BER');

シミュレーション結果

参考文献

• 高畑文雄, 前原文明, 笹森文仁. 「ディジタル無線通信入門」電波技術協会