はじめに
k-meansは教師なし学習に該当し、与えられたデータを任意の数のグループに分ける手法です。
本記事ではk-meansのアルゴリズムについて解説します。
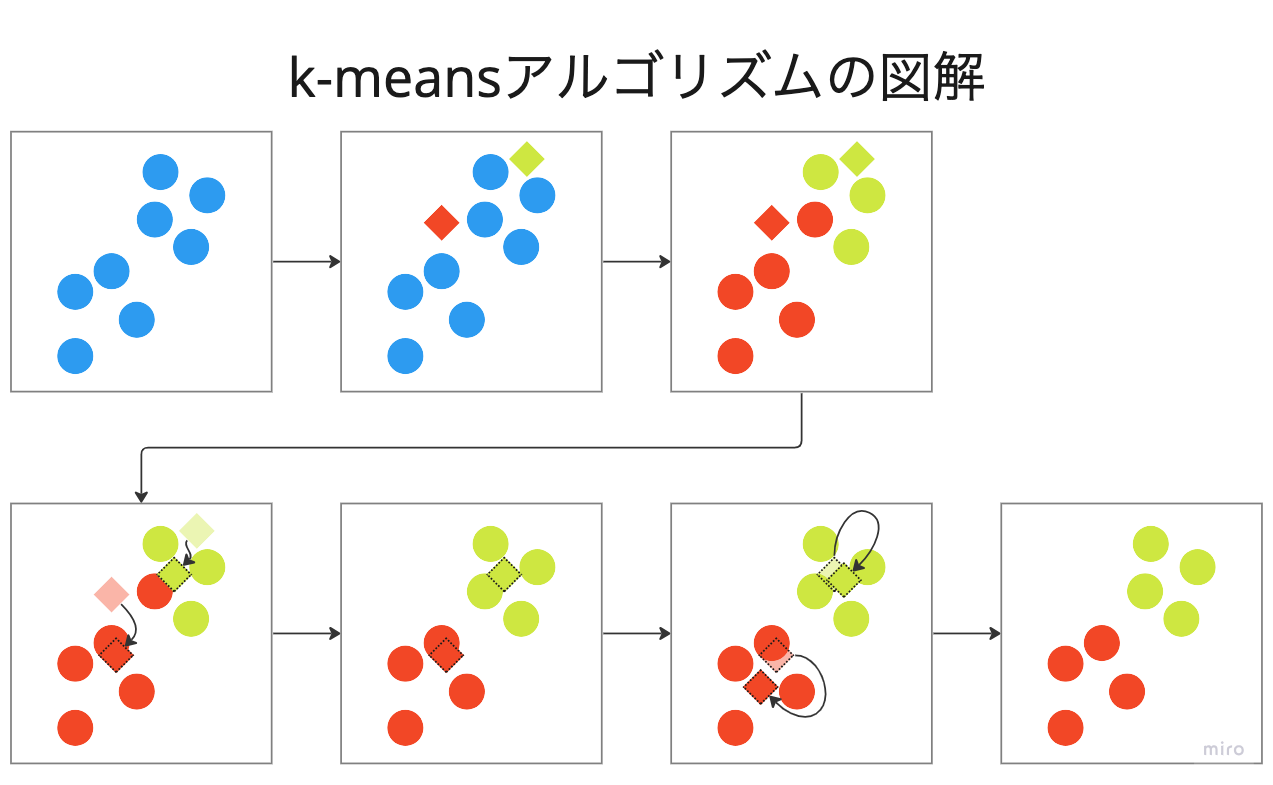
はじめに全体像をお伝えすると、下図のような処理を行っています。
1. k-meansについて
1.1. 概要
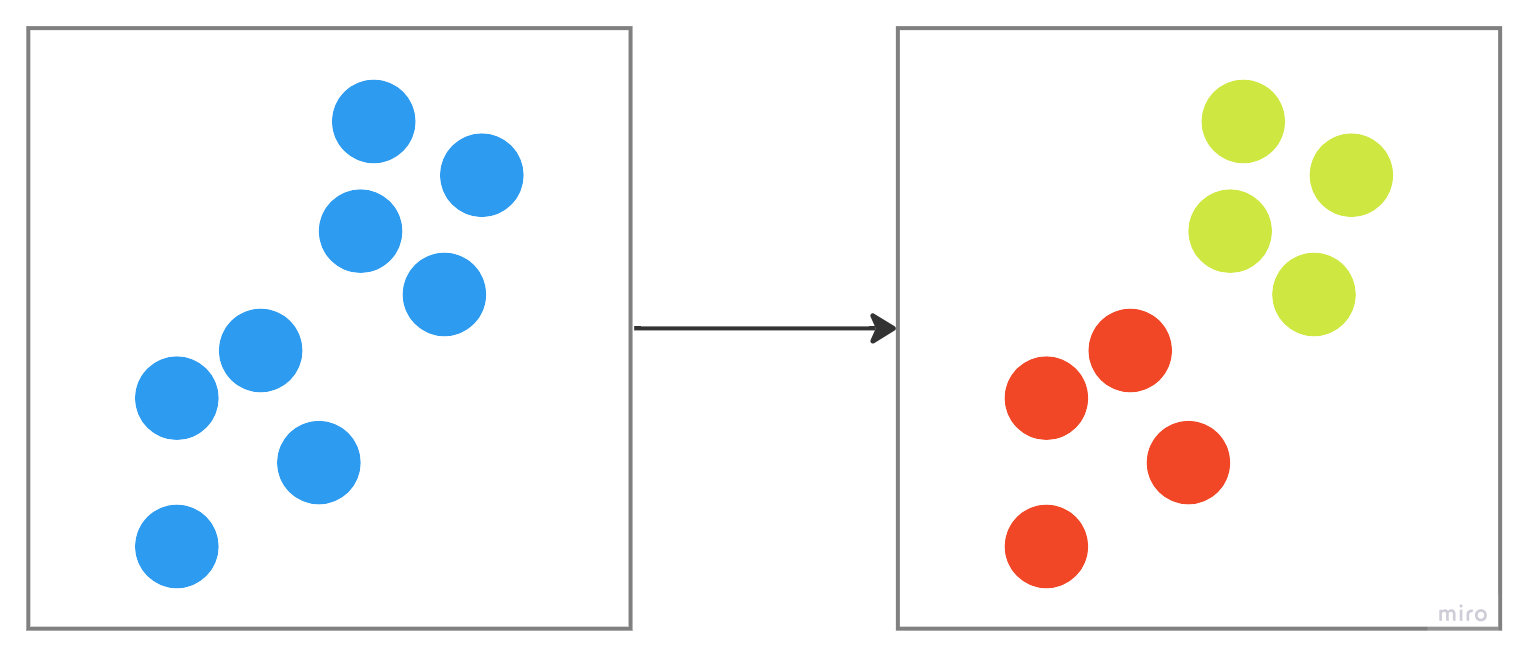
k-meansは、教師なし学習の一種で、与えられたデータをk個のクラスタに分割するアルゴリズムです。
ここでいう「クラスタ」とは、データの集合のことで、各クラスタ内のデータポイントは互いに似ているが、他のクラスタのデータポイントとは異なるという特性を持っています。
上図は、2つにクラスタリングする場合のイメージでして、あるアルゴリズムに従って、事前に決めた数のクラスタに分けてくれます。
1.2. アルゴリズムのステップ
k-meansの手順は大きく4つで、初期化・割り当て・更新・収束チェックです
以下では、簡単のために、2つのクラスタに分ける場合を図示します。
初期化
ランダムにセントロイド(クラスタの中心)$ C = {c_1, c_2,.....,c_k} $を選択します。
図では$k=2$の場合を考えているため、緑色と赤色のひし形で表現しています。
割り当て
ここでは各データポイント$x_j$に対して、どちらのクラスタに属するのかを割り当てます。
割り当ての方法としては、$x_j$から最も近い$c_i$を見つけ、そのクラスタを割り当てます。
このとき、距離の計算の方法はいくつかありますが、ユークリッド距離の二乗が使われることが一般的です。
$$d(x_j, c_i) = (x_j - c_i)^2 $$
更新
ここではセントロイドの更新を行います。
図では、各色のデータポイントの中心にひし形が移動しています。
クラスタの要素の数を$S$とすると、更新されたセントロイドの位置は以下のように表現できます。
$$ c{'}_i = \frac{1}{S} \sum{x_j} $$
収束チェック
クラスタ中心の更新による位置の変化がある閾値以下になるか、またはアルゴリズムが指定された最大繰り返し回数に達した場合に収束とみなします。
具体的には、すべての$i$に対して新旧のクラスタ中心間の距離が閾値$ϵ$以下になった場合です。
$$ (c{'}_i - c_i)^2 < ϵ $$
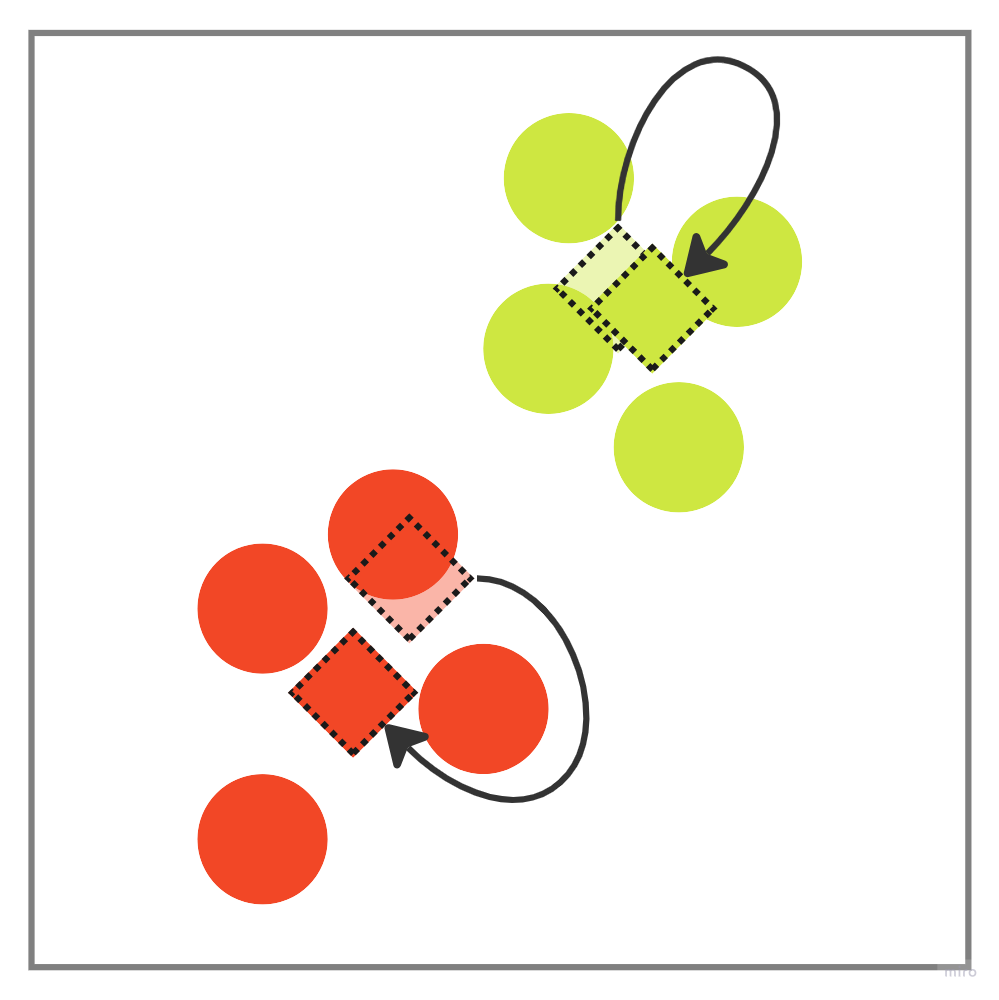
今回の場合だと、もう一度、割り当てと更新の処理をした方が良さそうです。
2回目の割り当てによって、赤色データポイントが緑色に変更され、
2回目の更新によって、データポイントの数が変わったため、セントロイドの位置が微調整されています。
クラスタ数の決め方
こうしたアルゴリズムを動かすよりも前に、クラスタ数kは決めないといけません。
その決めるための方法として、エルボー法がよく用いられます。
この方法では、クラスタ数を徐々に増やしていき、各kについてクラスタ内誤差平方和(SSE; Sum of Squared Errors)を計算します。SSEが大幅に改善しなくなる点、つまり「エルボー」と見なされるポイントが、最適なクラスタ数とされます。
k-meansの強みと弱み(限界)
強み
統計的なアプローチではなく、機械学習的なアプローチである点です。
クラスタリングする手法としてGMM(混合ガウス分布)も有名ですが、こちらは正規分布(ガウス分布)を仮定しています。
k-meansであれば、距離を計算するアプローチとなるため、どのような分布であっても機械的に計算が可能です。
弱み(限界)
- クラスタの形状とサイズ
- k-meansアルゴリズムは、クラスタの形状が球状であることを前提としています。
- そのため、非球状や長い形状をしたクラスタを正確に識別することが難しくなります。
- また、すべてのクラスタが同程度のサイズであることも暗黙の前提とされているため、大きく異なるサイズのクラスタが存在する場合、うまく機能しないことがあります。
- クラスタ数の指定
- k-meansを使用するには、あらかじめクラスタ数$k$を決定しておく必要があります。
- しかし、適切な$k$の値を見つけるのは、特にデータの構造が複雑な場合には困難です。
- エルボー法やシルエット法などの手法を用いて最適なクラスタ数を推定する方法がありますが、これらの方法でも常に完璧な$k$を決定できるわけではありません。
- 外れ値の影響
- k-meansは外れ値に非常に敏感です。
- 外れ値がクラスタの中心を大きくずらすことがあり、結果としてクラスタリングの品質が低下する可能性があります。
- 局所最適解の問題
- k-meansは初期クラスタ中心の選択に大きく依存しており、不適切な初期値が選ばれると、最適ではないクラスタリング結果に収束することがあります。
- この問題を緩和する方法の1つは、アルゴリズムを複数回実行し、最も良い結果を選択することです。
- ほかにも、k-means++という初期クラスタ中心をより賢く選択する方法もあります。
- k-means++では、最初の中心をランダムに選んだ後、次の中心を選ぶ際に、既存の中心からの距離に基づいて確率的に選択します。これにより、初期中心がデータセット内でより広く分散することが促され、局所最適解に陥るリスクが減少します。このアプローチは、全体的なクラスタリング品質の向上に寄与します。
終わりに
k-meansアルゴリズムは、その単純さと効率性から、多くのクラスタリングタスクに広く利用されています。
しかし、上記で述べた限界も理解しておくことが重要です。
これらの限界を踏まえつつ、データの特性や要件に応じて適切なクラスタリング手法を選択することが、成功への鍵となります。k-means以外にも、k-means++や階層的クラスタリング、DBSCANなど、様々なアルゴリズムが存在し、それぞれ異なる特性を持っています。