概要
- 公開鍵暗号、楕円曲線暗号とは
- 秘密鍵、公開鍵、BitCoinアドレスの関係
- それぞれの作成方法
公開鍵暗号
- 暗号化と復号に別々の鍵を使う暗号
- 公開鍵で暗号化、秘密鍵で復号
- 共通鍵暗号は暗号化と復号に同じ鍵を使う
- 鍵を安全に相手に渡せない問題=鍵配送問題
- 暗号化の鍵(公開鍵)を公開可能にすることで鍵配送問題を解決
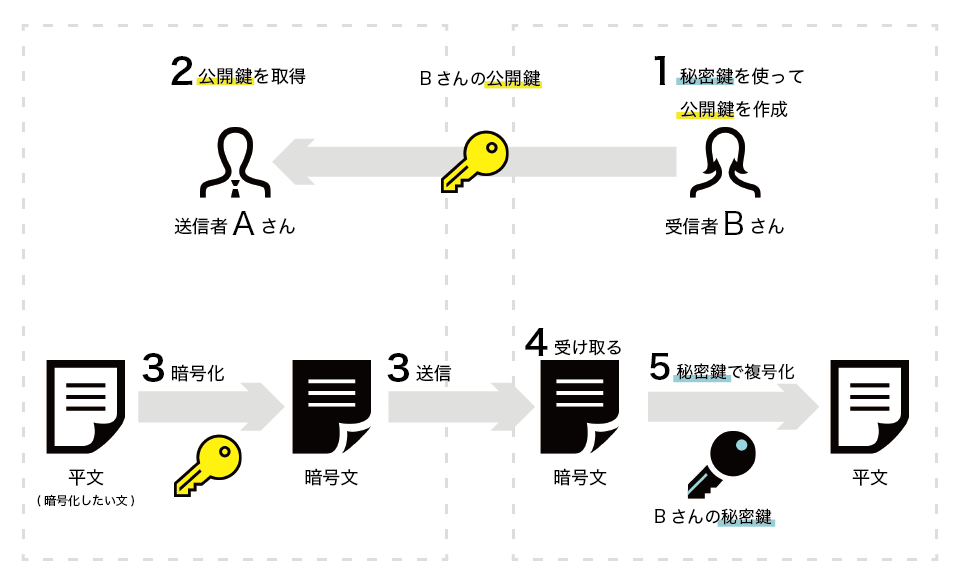
出典:udemy - 公開鍵暗号方式とは?初心者でもわかる公開鍵暗号方式の基礎
楕円曲線暗号
- 楕円曲線上の離散対数問題の困難性を利用した暗号
- ポストRSA暗号
- RSA暗号は素因数分解の困難性を利用した暗号
- RSA暗号と同等の安全性をより短い鍵で実現でき、処理速度も速い
- 楕円曲線DSA(ECDSA)、楕円曲線ディフィー・ヘルマン鍵共有(ECDH)、など
- 一部の楕円曲線では脆弱になる→安全な曲線の選定が大事
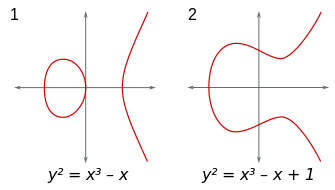
楕円曲線
- 指数
- その数が数 a の n 乗(an)で表される時の n
$$10^{4}=10000$$
- その数が数 a の n 乗(an)で表される時の n
- 対数
- 1でない正数aと正数Nとの間にN=a^bの関係がある時、そのb
$$log10\left( 10000\right) =4$$ - 普通は電卓でも計算可能
- 1でない正数aと正数Nとの間にN=a^bの関係がある時、そのb
- 楕円曲線上のある種の数の集合における特殊な対数(離散対数)では極端に計算が難しくなる
- イミフ
- だがそれが離散対数問題
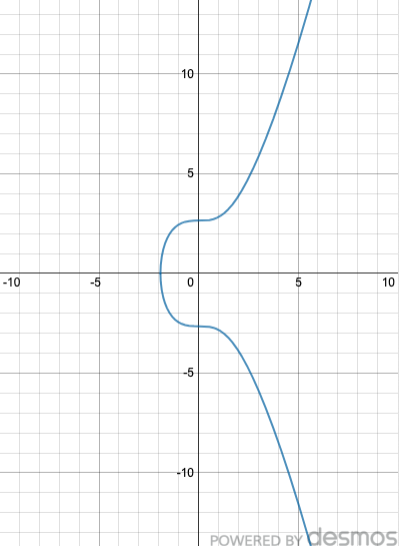
secp256k1
- SECGが定義した曲線とパラメータ
- 曲線
$$y^{2}=x^{3}+7$$ - 法となる素数
- ベースポイント
- SECG (Standards for Efficient Cryptography Group)
- 曲線
- BitCoinやEthereumで使われている
- AWS CloudHSMのJavaライブラリも対応している
- KMSの非対称鍵対応でも利用可能
- 他の曲線
- secp256r1
- NIST定義。NSAのバックドアある説(要出典)。
- secp256r1のほうがまだ安全
- Ed25519
- ツイストしたエドワーズ曲線暗号
- これは安全
- secp256k1やsecp256r1は弱いとDJBが言っていた
秘密鍵→公開鍵→BitCoinアドレス
- 秘密鍵
- ただの数値
- 256bitの秘密鍵はコインを256回投げれば生成できる
- 公開鍵
- 秘密鍵から生成される
- 楕円曲線上の点
- ビットコインアドレス
- 公開鍵から生成される
- ハッシュ値
秘密鍵
- 秘密にしなければならない鍵
- ただのランダムな数値
- 無量大数の10億倍くらい
- 人類が観測可能な宇宙に存在する原子より少し少ないくらい
- 銀河の全宇宙人が秘密鍵を毎ナノ秒1兆個ずつ50億年生成しても1/100京しか消費できない
- 数値の選び方が予測されないよう注意
- ランダム大事
- 256回コインを投げて表=0/裏=1で生成するのがベストプラクティス(要出典)
- 256bit/32byte/16進64文字
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
公開鍵
- 公開してもいい鍵
- 楕円曲線上のスカラー倍算を使って秘密鍵から生成される
- 楕円曲線上の点の座標を連結した数値
- x座標256bit + y座標256bit = 512bit/64byte/16進128文字
- ブロックチェーンではy座標を省略して容量削減してたりする(512bit→256bit)
- 方程式がy^2なのでx座標があれば解ける
- cofactorが1なので実際は4つ…みたいな話を見かけたがそっ閉じ
- yの+-を判定するフラグだけ別で持ってる
F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
公開鍵の生成
- 公開鍵は秘密鍵から作られる
- secp256k1で決められたベースポイント(曲線上の点G)
- 秘密鍵はただの数値k
- 点Gをk倍する→公開鍵(曲線上の点K)
- 点Gに掛け算ってどうやるのか?
- スカラー倍算
- 点Gをk回足し算するのと同じ
- G+G+G+G+...
- 点Gの足し算ってどうやるのか?
- G+G+2G+4G+8G+...
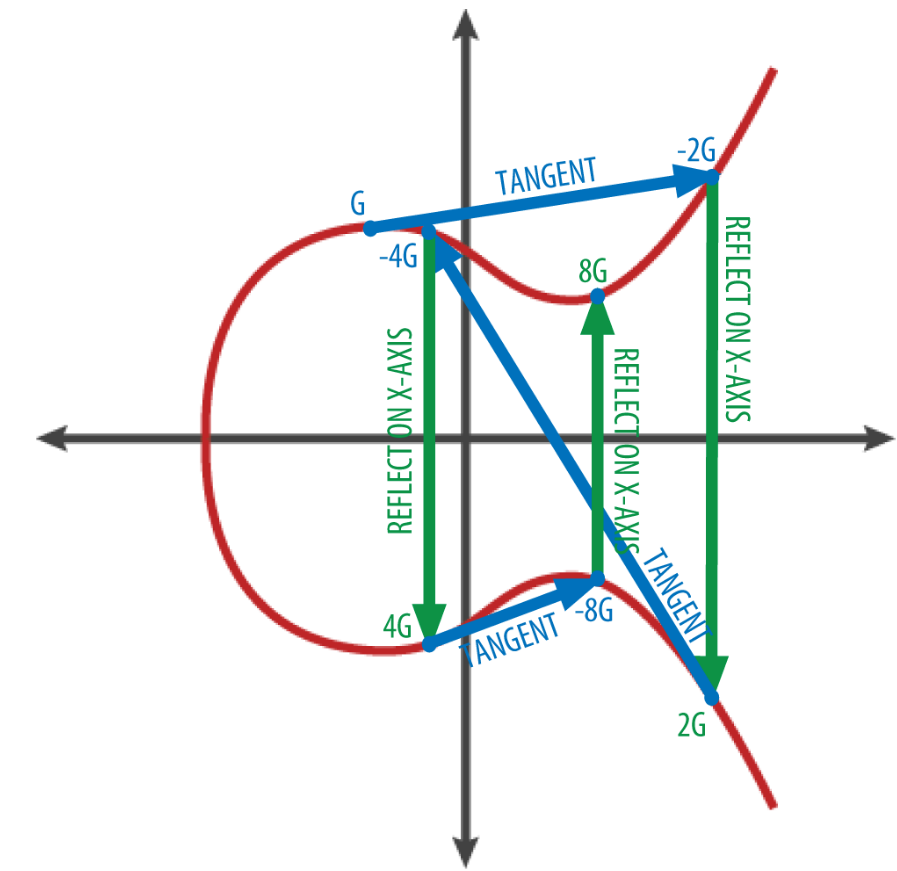
楕円曲線上のスカラー倍算
- 点A + 点Bの計算
- AとBを通る直線を引く
- 直線と楕円曲線の交点C
- Cをx軸に対して反転した点D
- A + B = D
- 点G + 点Gの計算
- Gの接線を引く
- 接線と曲線の交点-2G
- -2Gをx軸に対して反転した点2G
- G + G = 2G
- 上記の計算を繰り返す
- 2G + 2G = 4G
- 4G + 4G = 8G
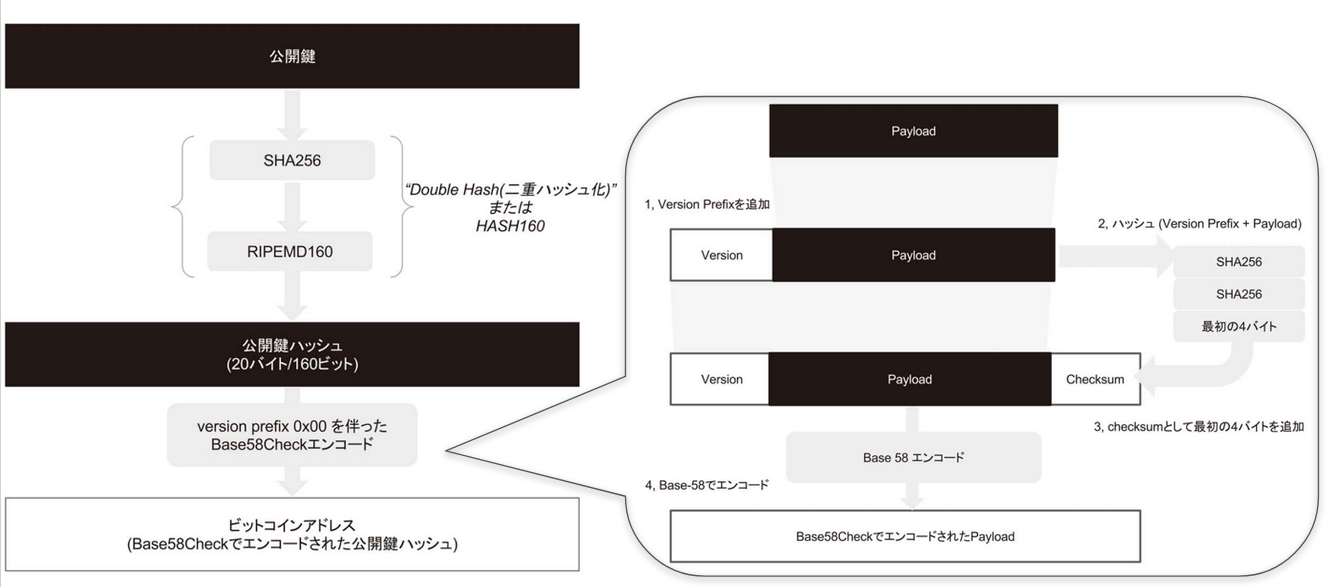
BitCoinアドレス
- 1番単純なアドレスは1から始まる文字列
- 公開鍵のハッシュ値をエンコードしたもの
- ハッシュ関数
- SHA256
- RIPEMD160
- エンコード
- Base58Check
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
まとめ
- 公開鍵暗号は鍵配送問題を解決した暗号
- 楕円曲線暗号はRSA暗号後の主流になる暗号
- 秘密鍵→公開鍵→BitCoinアドレスの順に不可逆に生成される
- つまり秘密鍵を漏らすと詰む
- 身近な利用例
- https
- ssh
- FIDO2
- セキュリティキー
- マイナンバーカード