$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
この記事は理物Advent Calender 2022の23日目の記事です。

0. はじめに

はじめまして、量子班に所属している理物3年のROTAGILLAと申します。

早いもので、2022年も残すところあと一週間ほどとなりました。サッカーワールドカップで日本が活躍するなど記憶に残る出来事がたくさんあった一年でしたが、何と言っても(!?)今年のハイライトは「Bellの不等式の破れ」に対してノーベル物理学賞が与えられたことでしょう。関連分野の皆さんがとても喜んでいらっしゃったのが印象的でしたね。

そこでこの記事では今年のノーベル賞のテーマとなった「量子もつれ」に関連する話で僕が面白いと思ったテーマをまとめてみました。具体的には、量子計算で重要なCNOTゲートがKitaevのToric Codeと呼ばれるモデルでどのように実現されるかを説明する記事となっています。個人的に、このテーマを学ぶうちに量子もつれの「もつれたる所以」を垣間見た気がしたので、皆さんにも少し考えてもらえると嬉しいです。(8. Braidingのところに書いてある内容です)

最近は何かと量子コンピュータが話題ですし、物理以外の人や高校生の方にもひょっとすると読んでもらえるかもしれない(!)と調子に乗った結果、量子力学の解説までしてしまいました。ですから、線形代数が少し分かる人であれば、適宜注釈も参照しつつ最後まで読めるようになっているはずです。もちろん、物理の人にもある程度面白いと思ってもらえるように書いています。

丁寧な説明を心がけた分ちょっぴり長い記事になってしまったと思わざるを得ませんが、よろしければお付き合いください。

1. 量子力学

まず、最低限必要な量子力学の知識について少し書きます。物理の人や、すでによく知っている人はこの章と次の量子もつれの章は読み飛ばしていただいて構いません。今回必要となる量子力学の知識は、以下の3つです。

1)状態はHilbert空間$\mathcal{H}$¹ (良い性質を持った複素線型空間と思えば大体OKです)の元$\ket{\psi}$²で表される。特に、状態の線形和(重ねあわせ)もまた状態として許される。

2)状態$\ket{\psi}$に対する測定とは、$\mathcal{H}$のある正規直交基底の組$e_{i}$に対して$\ket{\psi}$を射影することあり、どの基底ベクトルに射影されるかは確率的に定まる。その確率は$\ket{\psi}$を$e_{i}$で展開した係数³の絶対値の二乗に等しい。
特に、$\ket{\psi}$に対してエルミート演算子$\hat{A}$を測定する、とは$\ket{\psi}$を$\hat{A}$の固有ベクトルで作った正規直交基底に射影することである。測定の結果$\ket{\psi}$が$e_{i}$に射影されたならば、$\hat{A}$の固有ベクトル$e_{i}$に対応する固有値$a_{i}$が得られる。

3)二つの物理系をまとめて一つの物理系とみなす時はテンソル積を用いる。記号は$\otimes$。(独立な自由度を並列する記号だと思っておけばまぁ大体OKです)

以上で終わりです。(真面目に物理をやっている人が見たら怒りそうですが、そういう人はそもそもこの章は読まないでください)ただ、さすがにこれだけでは馴染みのない人はよくわからないと思うので、もう少し具体的に考えてみましょう。

<例１重ね合わせと射影測定>
2つの状態$\ket{0}, \ket{1}$をとる系(二準位系)があるとすると⁴、その線形和

\ket{\psi}=a\ket{0}+b\ket{1} \hspace{3mm}(a,b\in\mathbb{C}, \hspace{3mm}|a|^{2}+|b|^{2}=1)

もまたこの系の状態として許され、係数の絶対値の二乗$|a|^{2},|b|^{2}$はそれぞれ測定の結果$\ket{0}, \ket{1}$の状態を得る確率になります。仮に$a=b=\frac{1}{\sqrt{2}}$とするとこれは$\ket{0},\ket{1}$を$\frac{1}{2}$の確率でとる重ね合わせ状態(均等重ね合わせ状態)になります。

重ね合わせ状態に対する測定結果は必ず$\ket{0}, \ket{1}$のどちらかの状態となるのですが、測定を行うまではそのどちらの状態でもなくそれらが「重ね合わさった」状態です。ただし、測定でどちらの状態を得るかの確率は定まっているので、同一の重ね合わせ状態をたくさん集めて測定を行うと、得られる結果について定量的な予言をすることができます。

また、一度測定を行なって$\ket{0}$や$\ket{1}$などの状態を得ると、以降は同じ$\ket{0}, \ket{1}$基底で測定をするかぎり、最初に得られたのと同じ結果が出続けます。これは重ね合わせ状態が測定によって破壊された、とも言えます。量子状態は測定の影響を容易に受けてしまうのです。

<例2 テンソル積>
系Aで$\ket{0}$, 系Bで$\ket{0}$となっている状態をまとめて一つの系(合成系)とみなした状態は

\ket{0}\otimes\ket{0} \hspace{3mm}または省略して\ket{00}

と書きます。この記法を用いると、例えばAでの均等重ね合わせ状態とBでの均等重ね合わせ状態のテンソル積は

\frac{\ket{0}+\ket{1}}{\sqrt{2}}\otimes\frac{\ket{0}+\ket{1}}{\sqrt{2}}=\frac{\ket{00}+\ket{10}+\ket{01}+\ket{11}}{2}

のように計算され、$\ket{00}$をとる確率は$\frac{1}{2}$の2乗で$\frac{1}{4}$となります。

この辺りの話は去年のPhysicsLabでmanmaru_hukuroくんがより詳しくこちらにまとめてくれています。

2. 量子もつれ

さて、重ねあわせ、射影測定、テンソル積について説明したところで、例2 テンソル積と順番を逆にして、テンソル積を取ってから均等重ね合わせを行った

\ket{\psi}=\frac{\ket{00}+\ket{11}}{\sqrt{2}}

という状態(Bell状態)を考えてみましょう。これはAでの状態$\ket{\phi_{A}}$とBでの状態$\ket{\phi_{B}}$を一つの系とみなした結果得られた状態でしょうか？言い換えると、

\ket{\psi}=\ket{\phi_{A}}\otimes\ket{\phi_{B}}

と書けるでしょうか？実は、答えはNOです。(量子系に特有の性質である重ね合わせが元凶です。少し考えて確認してみてください。)このように、テンソル積に分解できない状態を「エンタングルした状態」、または「量子もつれ状態」などと呼び、色々と不思議な性質があります。

まず、テンソル積の形に分解できないということは、AやBのそれぞれの地点で局所的に状態が$\ket{\phi_{A}}$などと決められないことを含意しています。これは物理状態が局所的であるはずだという素朴な直感に反します。東京にある量子状態がNewYorkにある量子状態と切っても切れない関係にあるなどということは想像しにくいでしょう?でも、そういう状態が原理的にはありうるわけで、もっと近い距離ならば実験的にも確認されています。

さらに、エンタングルした状態の非局所性を利用すると、通信と組み合わせた一連の操作を行うことでAに存在する量子状態を勝手な場所Bに作り出す「量子テレポーテーション」を行うことができることも知られています。情報を送ることさえできればトラックに乗せて輸送したりしなくても、量子状態を事実上輸送(テレポート)できるというわけです。こうした性質はあのアインシュタインにとっても受け入れがたかったようで、彼はこれに関連した議論で量子力学に反論しています。(EPRパラドックスとして有名な話です。ちなみに、量子テレポーテーションでは通信が必要であり、通信速度は光速を超えないので相対論には矛盾しません)

この辺りの話は去年のPhyicsLabの解説記事でmatsumotoくんがより詳しくこちらにまとめてくれています。

3. CNOTゲート

さて、上述したことをかなり雑にまとめると、量子もつれ状態はなんか凄そうなわけです。「うまい話には裏がある」といいますから、量子もつれはそう簡単には生成できないように思われます。実際、量子もつれを生成するには光子を使う方法などがあるようですが、実験的にはなかなか面倒なプロセスを経ているようです。また、量子状態は測定によって破壊されてしまうので、量子もつれ状態を保つのも一苦労です。

ところが、多くの量子情報関連の授業や教科書では、量子もつれを生成するプロセスは以下のように簡単な図で済まされています。

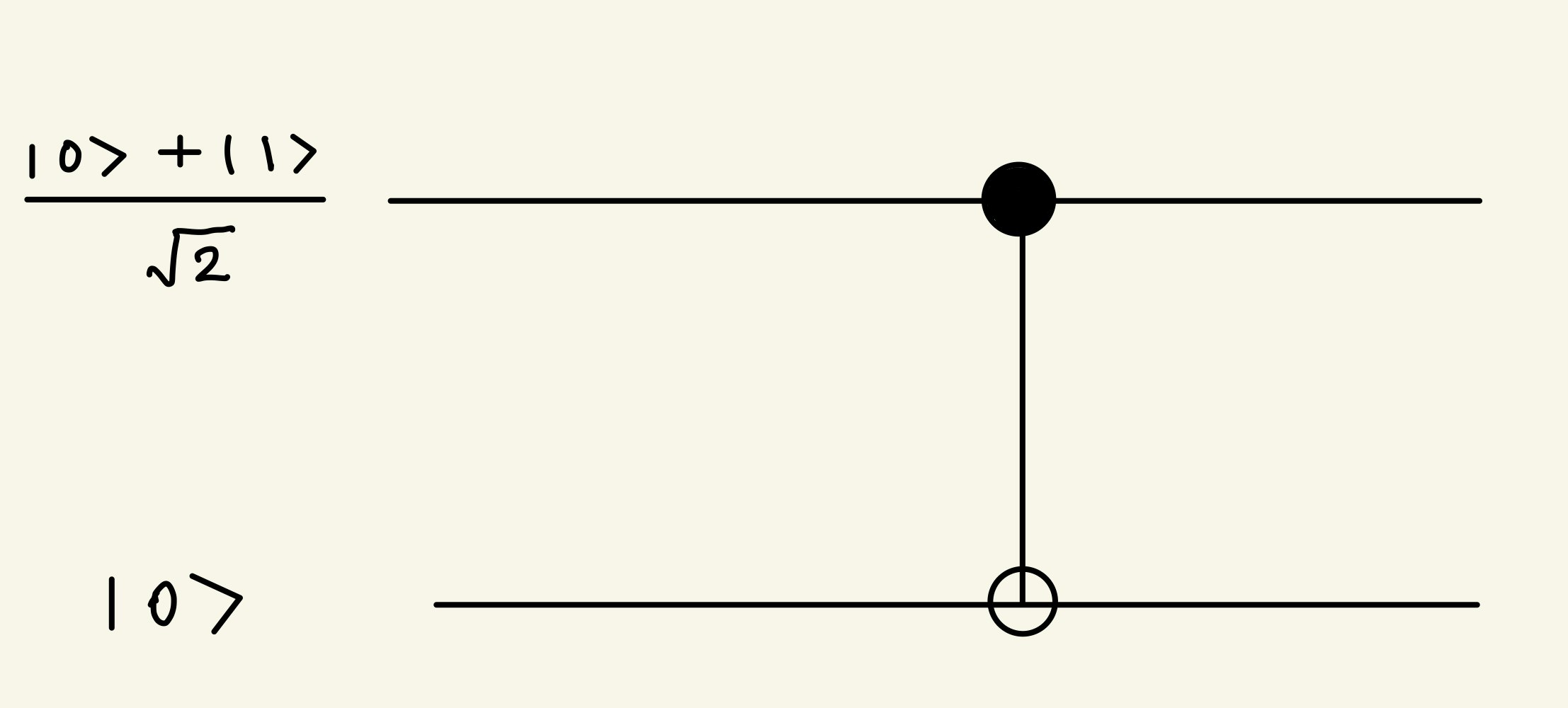
途中に出てきている黒丸と白丸の記号はCNOTゲートと呼ばれ、黒丸の量子ビットが$\ket{0}$状態なら何もせず、$\ket{1}$状態なら白丸の量子ビットを反転させる(=$\ket{0}$状態と$\ket{1}$状態を入れ替える)という操作です。実際、上の量子回路(左から右に読みます)を追っていくと、CNOTゲートをかける前の系の状態は

\ket{\psi} = \frac{\ket{0}+\ket{1}}{\sqrt{2}}\otimes \ket{0}

とテンソル積に分解できますが、CNOTゲートをかけるとBell状態

\ket{\psi} = \frac{\ket{00}+\ket{11}}{\sqrt{2}}

となるので、CNOTゲートのところでエンタングルメントが生成されていることが確認できます。そう考えるとCNOTゲートというのは結構すごいことをしているわけですが、図ではさも簡単そうに描かれています。なんか凄そうなはずのエンタングルメント生成がこんなに簡単に済んでしまうと、なんだか物足りなく思いませんか？少なくとも僕はどうも腑に落ちませんでした。CNOTゲートって、本当に実現できるの???

4. Toric Code

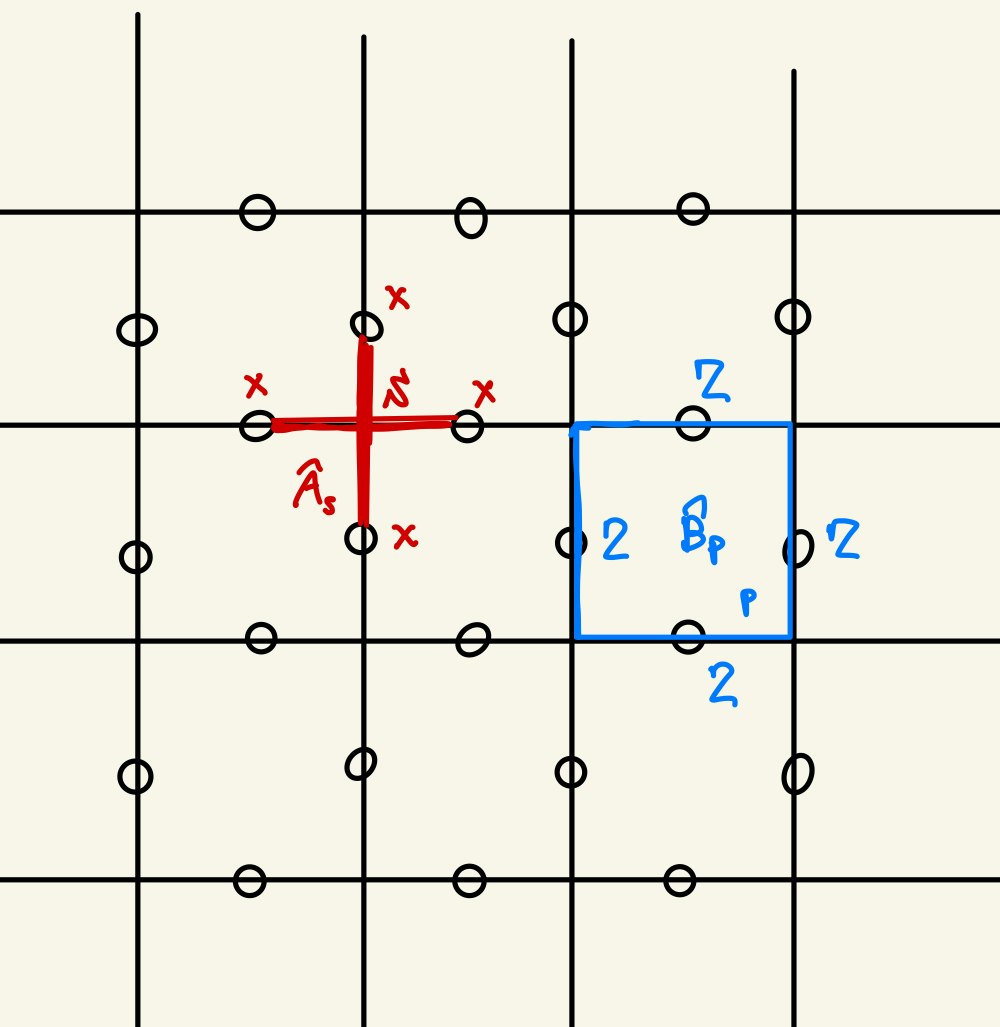
そこで登場するのがKitaevという物理学者によって提唱されたToric Codeと呼ばれる模型です。トーラス(またの名をドーナッツの表面といいます)の上に前述したような$\ket{0}=(1,0), \hspace{3mm}\ket{1} =(0,1)$の二つの準位をとる二準位系(以降、スピンと呼びます)をたくさん配置し、下図のように格子状に並べます。⁵

そして、以下のような演算子$\hat{A}$(Star演算子)と$\hat{B}$(Plaquette演算子)を考えます。

\hat{A}_{s} = \prod_{j\in \partial s} X_{j}, \hspace{3mm} \hat{B}_{p} = \prod_{j\in \partial p} Z_{j}

これらの演算子は上図ではそれぞれ赤と青に対応します。$\partial s$と$\partial p$はそれぞれ頂点sの再近接格子点と面pの境界上の格子点を表します。また、$X,Y,Z$はPauli行列と呼ばれるもので

X = 
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}, \hspace{3mm}
Y = 
\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix}, \hspace{3mm}
Z = 
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}, \hspace{3mm}

で定義されます。つまり、$\hat{A}_{s}$は頂点sの周りの4つの格子点にXをかける演算子、$\hat{B}$は面pの境界にある4つの格子点にZをかける演算子となっています。

これらの演算子を使って、ハミルトニアンと呼ばれる以下のような演算子を考えます。

\hat{H} = -J_{e}\sum_{s} \hat{A}_{s} -J_{m}\sum_{p} \hat{B}_{p}

ただし、$\hat{A}$についての和は全ての頂点$s$についてとり、$\hat{B}$についての和は全ての面$p$についてとります。このハミルトニアンの固有値が系のエネルギーとしてありうるものとなります。

唐突に変な系を考え始めて戸惑っているかもしれませんが、実はこのセットアップの元ではCNOTゲートを面白い方法で実現することができます。そしてそのプロセスを見ると、「量子もつれ」が文字通りの意味で「もつれ」なのではないかという気がしてきます。その感覚(錯覚?)を皆さんと共有するのがこの記事の本題で、8.Braidingの章にかいてあります。ただし、その前に準備としてStabilizer形式というものについて長々と説明しなければなりません。

5. Stabilizer形式

今までは量子状態をヒルベルト空間の元$\ket{\psi}$であらわしていましたが、これだと多自由度の系に対してテンソル積をたくさん並べて表現しなければならなくなり、不便です。そこでStabilizer形式では発想を転換して、演算子の組をまず定義し、その固有状態として状態を表現します。段階を追って概念に慣れていくことにしましょう。

5.1 群

まず、群について簡単に説明します。群というのは、かなり雑に言えば「まともな操作や作用の集合」のことです。(またしても真面目に勉強している人に怒られそうです、、、)具体的には、$x,y\in G$に対して演算$*$が定まり、

$x*y\in G$
$(x*y)*z =x*(y*z)$
単位元が存在
任意の$x\in G$に対して逆元が存在

という条件を満たす集合のことです。物理で出てくるようなまともな操作は多くの場合、なんらかの群をなします。

また、$G$の独立な元を何個かとってきて集合$I$を作り、Gの任意の元が$I$の元やその逆元同士の結合$*$を使って作れるとき、$G$は$I$によって生成されるといいます。そのような$I$のうち元の数が最小になるような作り方をしたときに$I$に含まれる元のことを、$G$の生成元と呼びます。もちろん、生成元自体は一意には定まりませんが、その数は定まります。線型空間の基底のようなものであると思えば大体OKです。

5.2 Pauli群

次に、Pauli群について説明します。恒等演算子IとPauli行列$X,Y,Z$(4. Toric codeで定義)の中から重複を許して$n$個の演算子(操作、作用ともいう)を選び、テンソル積を取ります。$n=3$のときはたとえば以下のようなやつがあります。

X\otimes Y\otimes X　\hspace{3mm} I \otimes X\otimes Z

(演算子のテンソル積の定義はしていませんでしたが、i番目の演算子はベクトルをテンソル積$\ket{\phi_{1}}\otimes\ket{\phi_{2}}\cdots \otimes \ket{\phi_{n}}$においてi番目のベクトル$\ket{\phi_{i}}$のみに作用すると考えます。独立な自由度を並列して書いていると思えば良いです。また、以降$X\otimes X$のことを$XX$などと略記します。)このような演算子に対して$\pm 1, \pm i$の4種類の係数を許したとき、ありうる組み合わせの全体は群をなし、これをPauli群$\mathcal{P}_{n}$と呼びます。

5.3 Stabilizer群、Stabilizer状態

ここでStabilizer群が定義できます。Pauli群$\mathcal{P}_{n}$の部分群⁶のうち、

[S_{i}, S_ {j}] = S_{i}S_{j}-S_{j}S_{i} = 0\hspace{3mm} for\hspace{3mm}  all \hspace{3mm} S_{i}, S_ {j}\in S_{n},  \hspace{3mm} 　-I\notin S_{n}

の条件を満たすものをStabilizer群$S_{n}$と言い、その任意の要素$S_{i}$に対して

S_{i}\ket{\psi} = \ket{\psi}

となる状態$\ket{\psi}$をStabilizer状態と言います。
Stabilizer群に入っている演算子はPauli行列のテンソル積なので、2乗すると$I$になるという性質があります。(確かめてみてください)従って$S_{i}\in S_{n}$の固有値を$\lambda$とすると、

\ket{\psi} = S_{i}^{2} \ket{\psi} = \lambda^{2} \ket{\psi}

となります。よって固有値は$\lambda=\pm1$のどちらかとなります。また、定義からStabilizer群に含まれる演算子は互いに可換かつエルミートであることがわかります。⁷なんだか言葉がたくさん出てきてよくわからないと思うので、具体例を見てみましょう。

<例3 Bell状態のStabilizer群>
$n=2$の時のStabilizer群の一つとして、$S = \{I, XX,ZZ, -YY \}$を考えましょう。これがStabilizer群の定義(可換かつ$-I\notin S$)を満たしていることは、$XZ=-iY=-ZX$や

(X\otimes X) (Z\otimes Z) = (XZ) \otimes (XZ) = (-ZX) \otimes (-ZX)=(Z\otimes Z)(X\otimes X)

などに注意すれば確認できます。また、この$S$は$\{XX,ZZ\}$によって生成されることがわかります。実際、

(X\otimes X) (X\otimes X) = X^{2} \otimes X^{2} = I \otimes I =I

(X\otimes X) (Z\otimes Z) = (-iY) \otimes (-iY) = -Y \otimes Y

です。さらに、対応するStabilizer状態はBell状態

\ket{\psi}=\frac{\ket{00}+\ket{11}}{\sqrt{2}}

になります。実際、Pauli行列Xは$\ket{0} =(1,0)$と$\ket{1} =(0,1)$を入れ替える役割を持つので、

(X\otimes X)\ket{\psi}=\frac{\ket{11}+\ket{00}}{\sqrt{2}} = \ket{\psi}

です。また、Pauli行列Zは$\ket{i}$ を$(-1)^{i}$倍する役割を持つので、

(Z\otimes Z)\ket{\psi}= \frac{\ket{00}+(-1)^{2}\ket{11}}{\sqrt{2}}=\ket{\psi}

となって確かに$S_ {i}\ket{\psi} =\ket{\psi}$です。

5.4 Stabilizer空間

続いて、Stabilizer空間とその次元についてざっくり説明します。
Stabilizer群を決めたとき、対応するStabilizer状態全体のなすHilbert空間のことを、Stabilizer空間といいます。前節まででみたように、Stabilizer群に含まれる演算子(Stabilizer)の固有値は+1か-1のどちらかです。従って、Stabilizer群に新しく独立なStabilizer $\hat{S}$ を一つ追加するたびに、対応するStabilizer空間は$\hat{S}$の固有値が+1の部分と-1の部分の二つに分割されていきます。(下図)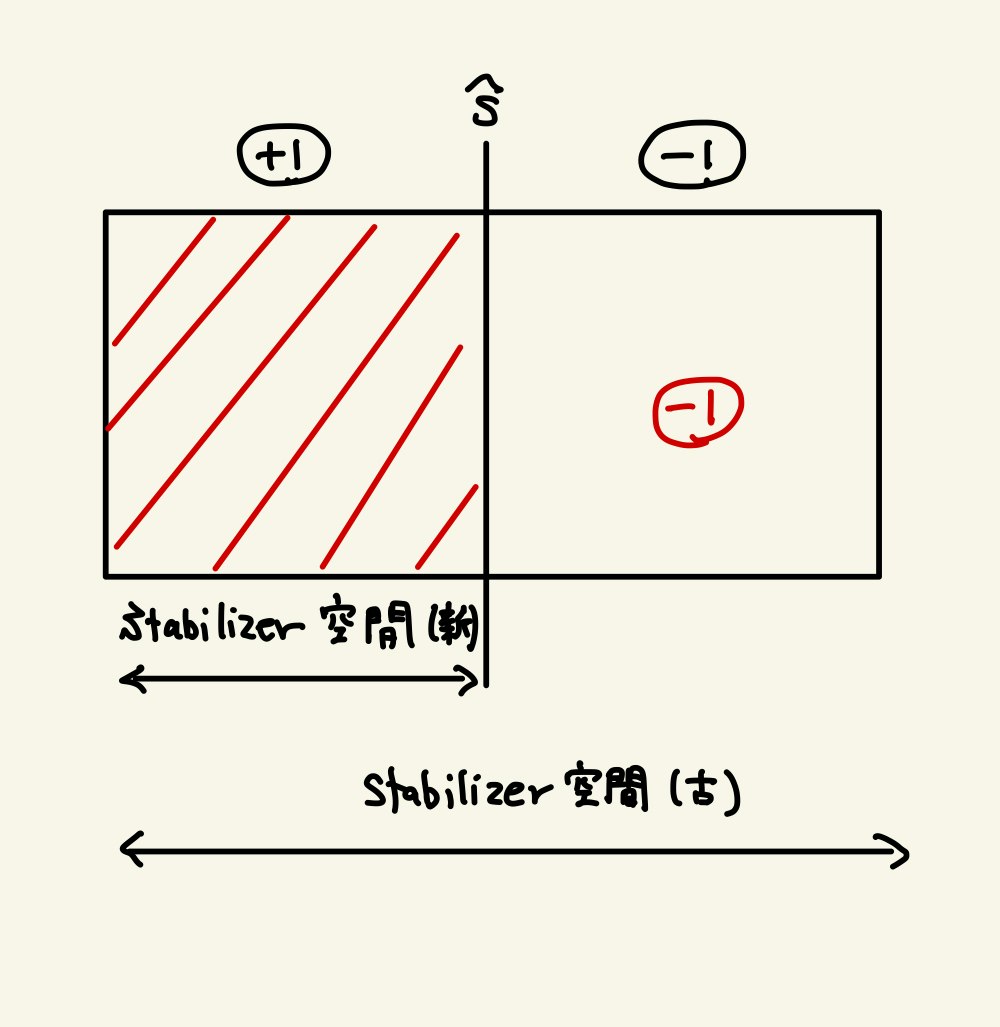

$n$個のQubitからなる系のHilbert空間の次元は$2^n$ですから、生成元(独立なStabilizer)を$k$個定義すると空間は$2^k$個に分割されて、Stabilizer空間の次元は$2^{n-k}$になります。

5.5 Logical Operator, Logical Qubit

続いて、Logical OperatorとLogical Qubitについて説明します。"Logical"というのは「事実上の」とか「概念上の」といったような読み替えをすれば大体OKだと思います。例えば、通常の古典コンピュータでも"0"という内容を伝える際には冗長性を持たせて"00000"などと符号化したりしますよね。このとき、実際に送っている符号は"00000"ですが、これは概念としては"0"を表しています。量子計算でも同様にして、「Logicalな」Pauli行列や「Logicalな」Qubitを考えることができます。具体例で見てみましょう。

<例4 5量子ビットコード>
5個のQubitからなる系に対して4個のStabilizer

S_{1} = ZXXZI\\
S_{2} = IZXXZ\\
S_{3} = ZIZXX\\
S_{4} = XZIZX\\

を定義します。⁸Stabilizerが4個あるので、Stabilizer空間の次元は$2^5/2^4 =2 $となります。ここで$X_{L}=XXXXX, Z_{L}= ZZZZZ$という演算子を考えてみましょう。これは$S_{i}$とは可換かつ独立で、Pauli群$\mathcal{P}_{5}$の元になっています。5.4 Stabilizer空間の議論と同様にしてStabilizer空間は$Z_{L}$の固有値が+1の部分(1次元)と-1の部分(1次元)に分けることがことができるので、

Z_{L}\ket{0}_{L} = \ket{0}_{L}\\
Z_{L}\ket{1}_{L} = -\ket{1}_{L}\\

によって$\ket{0}_{L}, \ket{1}_{L}\in \mathcal{H}$を定義することができます。すると、これらがLogicalなPauli X,ZやLogicalな$\ket{0}, \ket{1}$となっています。実際、$X_{L}Z_{L}=-Z_{L}X_{L}$より

Z_{L}(X_{L}\ket{0}_{L}) = -X_{L}Z_{L}\ket{0}_{L}=-X_{L}\ket{0}_{L}\\
Z_{L}(X_{L}\ket{1}_{L}) = -X_{L}Z_{L}\ket{1}_{L}=X_{L}\ket{1}_{L}\\

なので、

X_{L}\ket{0}_{L} = \ket{1}_{L}\\
X_{L}\ket{1}_{L} = \ket{0}_{L}\\

であることがわかります。よってLogical Qubitに対するLogicalなPauli行列の作用は、通常のPauli行列と同様であることがわかります。

5.6 Stabilizer形式における測定

続いて、Stabilizer形式における測定について説明します。ここでは、あるStabilizer群を指定し、対応するStabilizer状態に対してPauli群の演算子$P$の測定を考えます。1.量子力学で説明したように、「演算子$P$の測定を行う」とは、$P$の固有状態で張られた正規直交基底に状態を射影することでした。従って、一般には測定の前後で状態が変化するわけです。実際、$P$の固有値+１の固有空間への射影を行う演算子を$\mathcal{P}_{+}$, -1の固有空間に対して射影を行う演算子を$\mathcal{P}_{-}$とすると、

I = \mathcal{P}_{+} + \mathcal{P}_{-}\\
P = \mathcal{P}_{+} - \mathcal{P}_{-}\\

です。よって、$P$の測定結果が+1, -1であるとき、測定前のStabilizer状態$\ket{\psi}$はそれぞれ

\mathcal{P}_{+} \ket{\psi} = \frac{I+P}{2} \ket{\psi}\\
\mathcal{P}_{-} \ket{\psi} = \frac{I-P}{2} \ket{\psi}\\

へと変化することがわかります。
これにともない、対応するStabilizer群も変化します。測定前のStabilizer群の元$S_{i}$を一つとり、それが測定後の状態に対してもStabilizerになっているかを考えましょう。$P$はPauli群の元なので、$S_{i}$と$P$は交換するか反交換するかで場合分けができます。(Pauli行列の代数を思い出しましょう)

まず、$S_{i}$と$P$が交換する場合を考えます。このとき、

S_{i}\mathcal{P}_{+} = \mathcal{P}_{+} S_{i}\\
S_{i}\mathcal{P}_{-} = \mathcal{P}_{-} S_{i}\\

なので

S_{i}(\mathcal{P}_{+} \ket{\psi})= \mathcal{P}_{+}S_{i}\ket{\psi}　= \mathcal{P}_{+}\ket{\psi}\\
S_{i}(\mathcal{P}_{-} \ket{\psi})= \mathcal{P}_{-}S_{i}\ket{\psi}　= \mathcal{P}_{-}\ket{\psi}\\

となり、$S_{i}$は測定後もStabilizerであることがわかります。
次に、$S_{i}$と$P$が反交換する場合を考えます。このとき、

S_{i}\mathcal{P}_{+} = \mathcal{P}_{-} S_{i}\\
S_{i}\mathcal{P}_{-} = \mathcal{P}_{+} S_{i}\\

なので

S_{i}(\mathcal{P}_{+} \ket{\psi})= \mathcal{P}_{-}S_{i}\ket{\psi}　=
\mathcal{P}_{-}\ket{\psi}\\
S_{i}(\mathcal{P}_{-} \ket{\psi})= \mathcal{P}_{+}S_{i}\ket{\psi}　= \mathcal{P}_{+}\ket{\psi}\\

固有値が異なる空間の元は直交するので、どちらの場合も$S_{i}$は測定後にはもはやStabilizerではなくなっていることがわかります。その代わり、

P\mathcal{P}_{+} = P\left(\frac{I+P}{2} \right)= \left(\frac{P+I}{2} \right) = \mathcal{P}_{+}\\
-P\mathcal{P}_{-} = -P\left(\frac{I-P}{2} \right)= \left(\frac{-P+I}{2} \right) = \mathcal{P}_{-}\\

なので、

P(\mathcal{P}_{+} \ket{\psi})= \mathcal{P}_{+}\ket{\psi}　\\
-P(\mathcal{P}_{-} \ket{\psi})= \mathcal{P}_{-}S\ket{\psi}\\

となります。従って、測定結果が+1ならば$S_{i}$の代わりに$P$が、-1ならば$S_{i}$の代わりに$-P$が新たにStabilizerになることがわかります。具体例で見てみましょう。

<例5 Bell状態の測定とStabilizer群>
例3 Bell状態のStabilizer群で見たように、Bell状態のStabilizer群は$XX, ZZ$によって生成されます。ここで、$ZI$の測定を行いましょう。(物理的には1つ目のqubitのスピンの$z$成分を測定するということです。)$ZZ, ZI$は交換するので、測定後も$ZZ$はStabilizerです。一方、$XX, ZI$は反交換するので$XX$はStabilizer群から消え、測定結果が+１ならば$ZI$が、測定結果が−１ならば$-ZI$が代わりにStabilizerになります。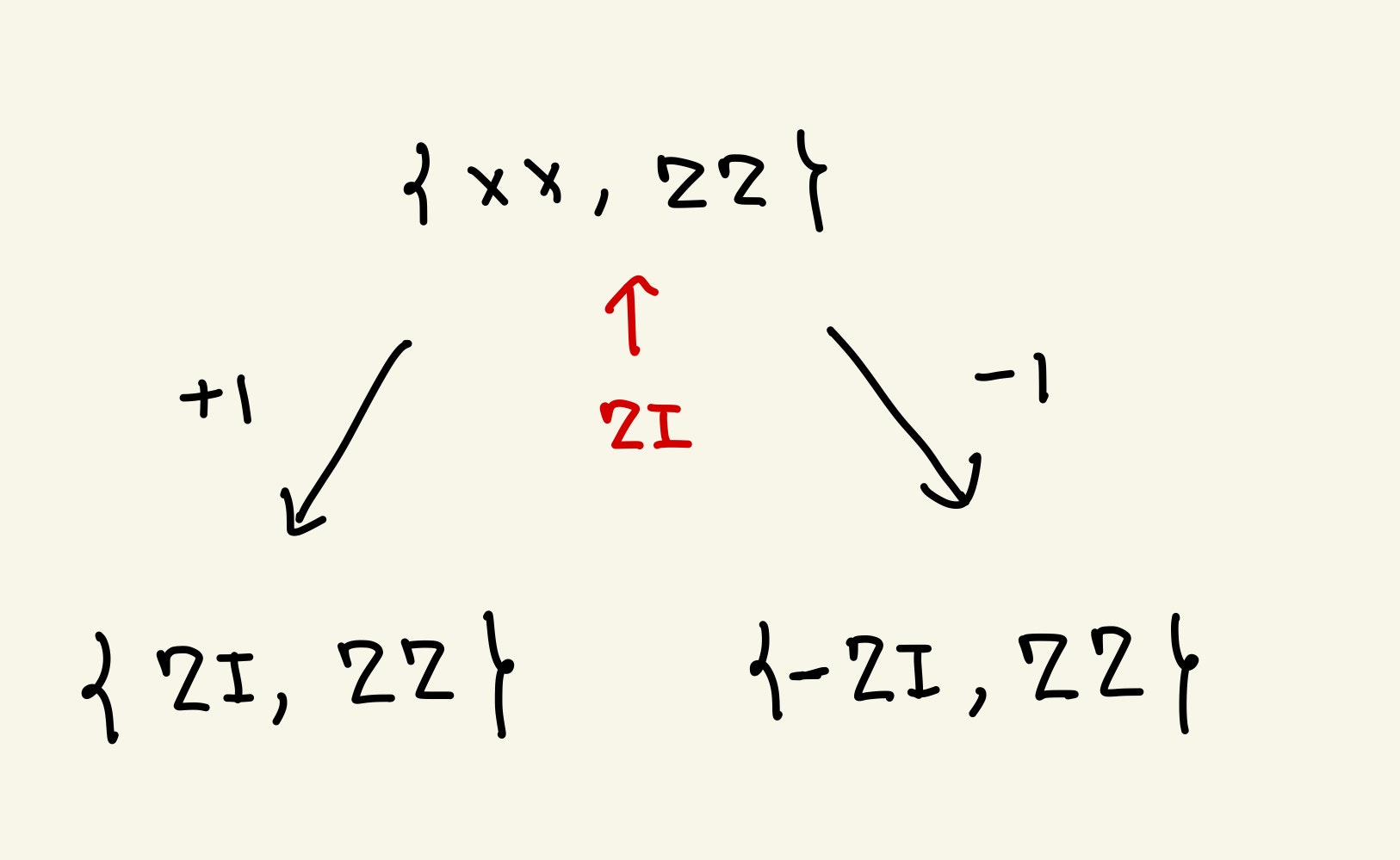

5.7 CNOTゲート再考

最後に、Stabilizer形式の精神に則って、CNOTゲートが演算子$X,Z$などに対してどのように作用するかを考えてみましょう。それには、$\ket{00}, \ket{01}, \ket{10}, \ket{11}$に対する作用を具体的に考えれば良いです。たとえば、

U_{CNOT} (X\otimes I)\ket{00} = U_{CNOT}\ket{10} = \ket{11}\\
U_{CNOT} (X\otimes I)\ket{01} = U_{CNOT}\ket{11} = \ket{10}\\
U_{CNOT} (X\otimes I)\ket{10} = U_{CNOT}\ket{00} = \ket{00}\\
U_{CNOT} (X\otimes I)\ket{11} = U_{CNOT}\ket{01} = \ket{01}\\

(X\otimes X)U_{CNOT}\ket{00} = X\otimes X\ket{00} = \ket{11}\\
(X\otimes X)U_{CNOT}\ket{01} = X\otimes X\ket{01} = \ket{10}\\
(X\otimes X)U_{CNOT}\ket{10} = X\otimes X\ket{11} = \ket{00}\\
(X\otimes X)U_{CNOT}\ket{11} = X\otimes X\ket{10} = \ket{01}\\

なので

U_{CNOT} (X\otimes I)=(X\otimes X)U_{CNOT}

となります。同様にして、

U_{CNOT} (X\otimes I)=(X\otimes X)U_{CNOT}\\
U_{CNOT} (I\otimes X)=(I\otimes X)U_{CNOT}\\
U_{CNOT} (Z\otimes I)=(Z\otimes I)U_{CNOT}\\
U_{CNOT} (I\otimes Z)=(Z\otimes Z)U_{CNOT}\\

がわかります。

6. Toric CodeのLogical Qubit(基本編)

さて、だいぶ長い準備でしたが、話をToric codeに戻しましょう。量子計算を実現するにあたっては、何はともあれLogical Qubitを用意しないと話が始まりません。実はToric Codeの基底状態(最低エネルギー状態)の張る空間は4次元であり、(物理の言葉で言えば4重縮退)、これを使うと2つ分のLogical Qubitを用意することができます。(2自由度$\times$2で4次元)

まず初めに、Toric CodeをStabilizer形式の視点から眺め直してみましょう。Star演算子$\hat{A}$とPlaquette演算子$\hat{B}$は

\hat{A}_{s} = \prod_{j\in \partial s} X_{j}, \hspace{3mm} \hat{B}_{p} = \prod_{j\in \partial p} Z_{j}

で定義されたのでした。これはよく見るとPauli群の元になっており、しかも$\hat{A}_{s}$同士、$\hat{B}_{p}$同士は$X^2=Z^2=I$なので交換します。また、$\hat{A}$と$\hat{B}$が十分離れていてスピンを共有しなければお互いに関係ないので交換しますし、仮に交わっていても下図のように必ず2ヶ所で交わっています。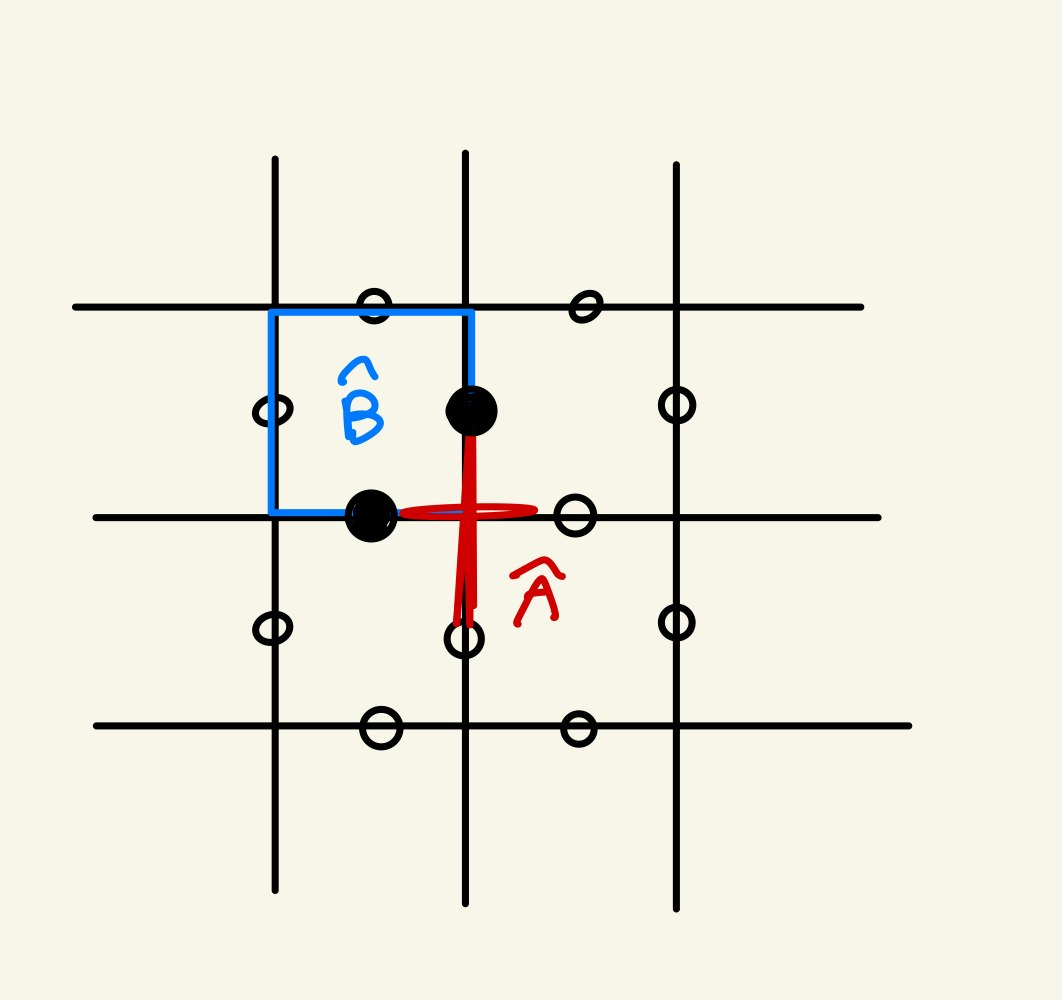

よって$XZ=-ZX$から出てくる符号反転が2回生じ、$\hat{A}$と$\hat{B}$は結局交換することがわかります。それに、$\hat{A}, \hat{B}$は全てエルミートです。以上より、Star演算子とPlaquette演算子によって生成される群はStabilizer群となることがわかります。

また、対応するStabilizer状態は、ハミルトニアン

\hat{H} = -J_{e}\sum_{s} \hat{A}_{s} -J_{m}\sum_{p} \hat{B}_{p}

の各項を最小にする(Star演算子、Plaquette演算子の固有値は$\pm1$のどちらかであることに注意)ので、物理の言葉で言うと基底状態になっていることがわかります。

では、Stabilizer空間の次元はどうなっているでしょうか。トーラスの一周には$N$個のスピンが配置されていると考えると、ヒルベルト空間の次元は$2^{2N^2}$となります。(格子1つあたりのスピンの数は2つ)また、生成元はStar演算子とPlaquette演算子です。ただし、全てのPlaquette演算子をかけるとそれぞれのスピンのところで2回$Z$がかかり

\prod_{s} \hat{B}_{s}　=I

となるので、Plaquette演算子のうち独立なものは面の数$F-1$となります。同様にして、Star演算子のうち独立なものは頂点の数$V-1$となります。Eulerの多面体定理より、トーラスの種数(穴の数)をgとすると

V-E+F=2-2g

なので、生成元の数は$V+F-2=2N^2-2g$となります。ここでは$g=1$なので、5.4 Stabilizer空間の議論を使うと、Stabilizer空間の次元は$2^{2N^2}/2^{2N^2-2}=4$となり、冒頭で述べた結果を得ることができました。

そこで、この4次元のStabilizer空間をPauli群に含まれる何らかの演算子$\hat{O}$の固有値で分類して分割することができれば、それぞれの状態をLogical Qubitとして使えるのではないかと考えられます。そのような分類が可能になるためには$\hat{O}$が任意のStabilizerと同じ基底で対角化できなければなりません。線形代数で学んだように、それは$\hat{O}$が任意のStabilizerと交換することと同値です。ただし、$\hat{O}$自体がStabilizer群の元だとStabilizer状態$\ket{\psi}$に対して自明な作用しかしない($\hat{O}\ket{\psi}=\ket{\psi}$)ので、結局

全てのStabilizerと交換し、かつそれらと独立なPauli群の演算子(=Logical Operator)を見つける

ことがLogical Qubitを構成するために必要であるとわかります。(名前の由来は後で納得できるはずです)そこで、以下のように連続したスピンについて$Z$のテンソル積をとった$Z$Chainを考えてみましょう。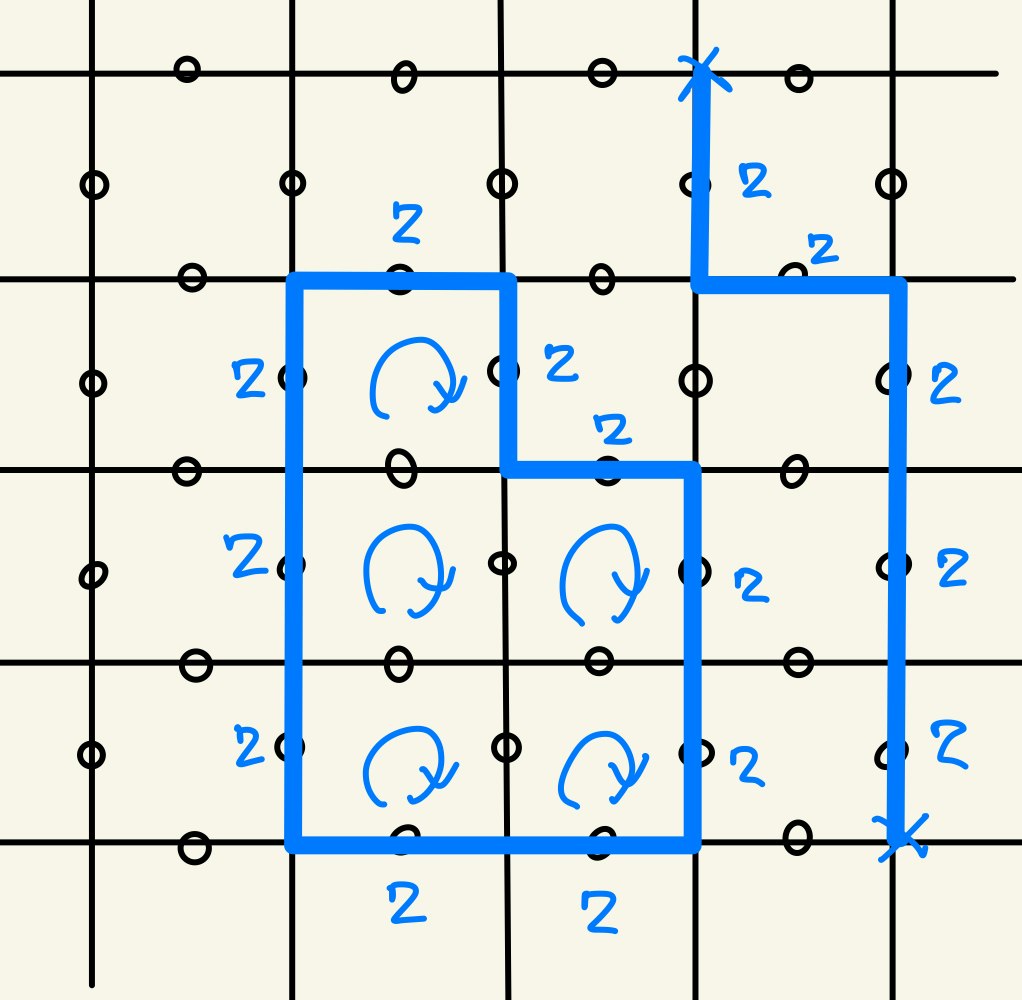

右側のように境界がある開いたChainでは、端の点(バツ印のところ)でStar演算子と反交換してしまうため、条件を満たしません。一方、左側のような閉じたChainはStar演算子と0または2個のスピンを共有するので、全てのStar演算子やPlaquette演算子と交換します。しかし、図のように境界の内側のPlaquette演算子同士の積を考えると、内側では$Z$が２回かかって打ち消し合うため、

\prod_{i\in \partial p} Z_{i}=\prod_{p} \hat{B}_{p}

となります。(コーシーの積分定理やストークスの定理を知っている方には見覚えのある変形でしょう。高校生の方であれば、和の中抜けや微分積分学の基本定理を思い出すと少し近いと思います。)つまり、$Z$Chainの演算子はStabilizerと独立ではなくなってしまいます。ではどうすれば良いのでしょうか?実は、下図のようなChainを考えると、条件が満たされます。

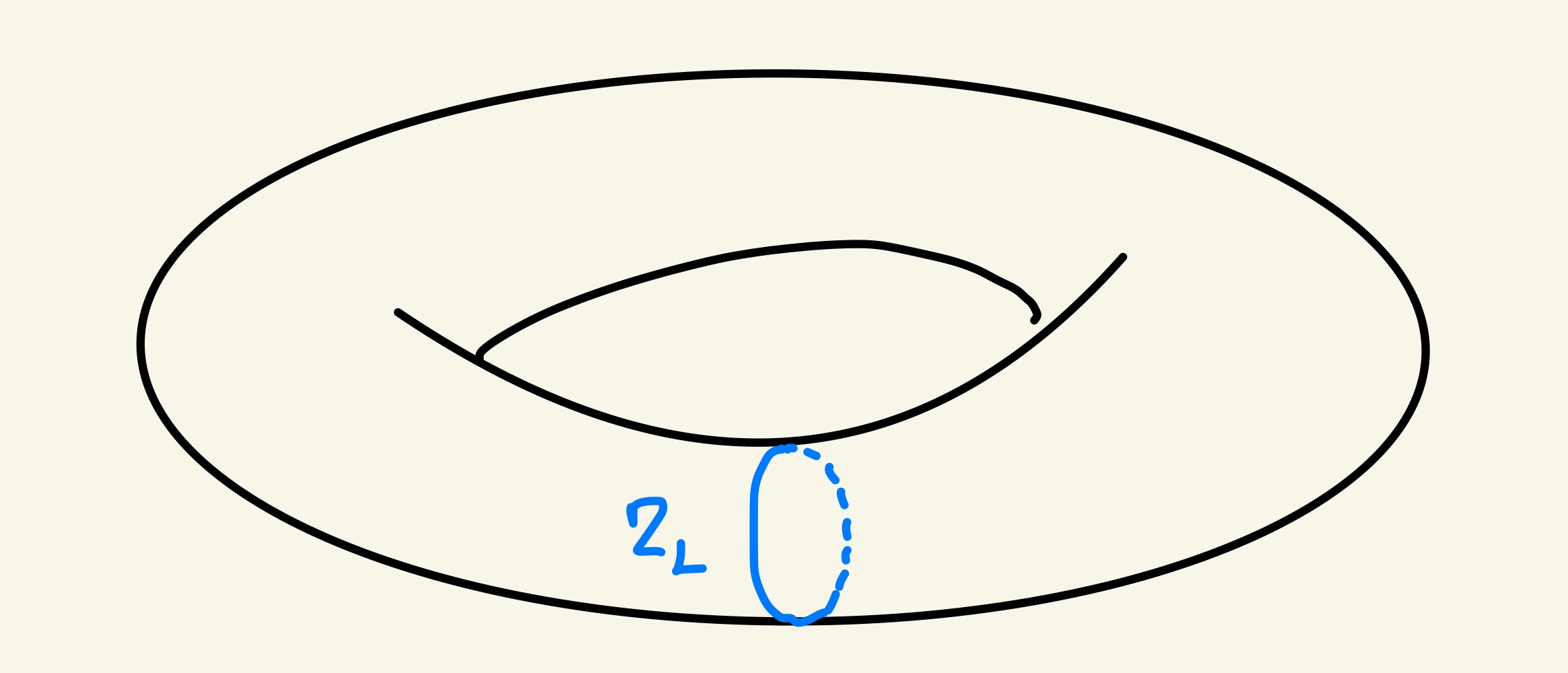
そう、トーラスに巻きつくループを考えれば境界がなく、かつStabilizerと独立な演算子$Z_{L}$になっています。同じことが$X$のテンソル積をとった$X$Chainについても考えられます。トーラスの独立なループは2つあり、$Z$Chainと$X$Chainのどちらを選ぶかの2通りがあるので、合計4つのLogical Operatorが見つかりました。

特に、下図のように一ヶ所で交わる$X$chainの$X_{L}$と$Z$Chainの$Z_{L}$の組み合わせを考えると、それらは互いに反交換し、LogicalなPauli$X, Z$になっていることがわかります。

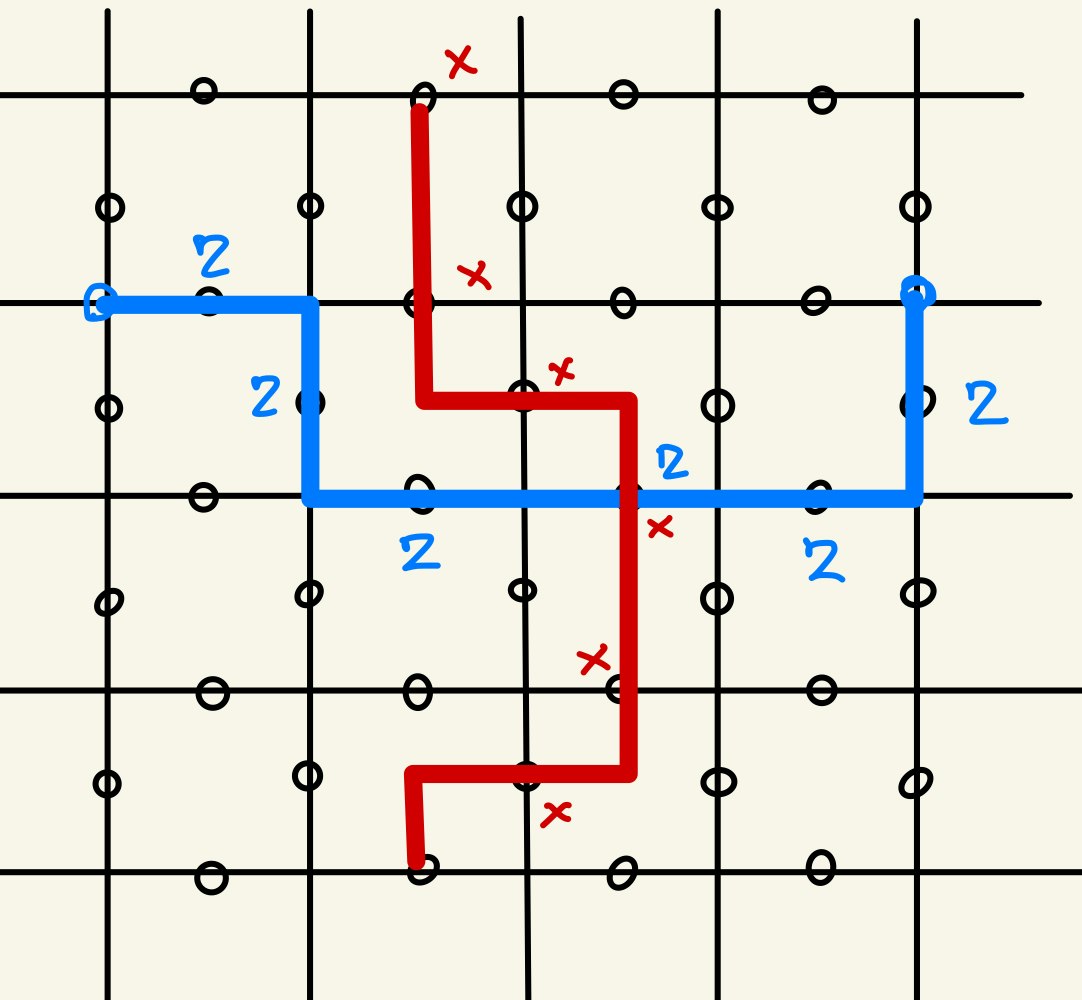
これで準備が整ったので、具体的に1bitのLogical Qubitを構成してみましょう。$Z_{L}$と独立なもう一方の$Z$chain、$\tilde{Z}_{L}$の固有値が+1となるStabilizer空間の部分集合$\mathcal{H}_{0}$を考えましょう。5.4 Stabilizer空間の次元の議論と同様にして、$\mathcal{H}_{0}$の次元は2となります。そこで、$\mathcal{H}_{0}$に属する状態のうち、$Z_{L}$固有値が+1の状態を$\ket{0}_{L}$とし、固有値が-1の状態を$\ket{1}_{L}$とすれば、$X_{L}, Z_{L}$は反交換するので、例4 5量子ビットコードでの議論と同様にして$X_{L}\ket{0}_{L}=\ket{1}_{L}, \hspace{3mm} X_{L}\ket{1}_{L}=\ket{0}_{L}$となり、確かに1bitのLogical Qubitが構成できたことがわかります。

また、わざわざ上記のように考えなくとも、Logicalな$X,Z$のペアが二つ構成できたので、Stabilizer空間は$\ket{00}_{L}, \ket{01}_{L}, \ket{10}_{L}, \ket{11}_{L}$で張られる、と直接的に考えることもできます。

7. Toric CodeのLogical Qubit(発展編)

前節でみたように、Stabilizer空間の自由度を使ってLogical Qubitを作るというのが基本的なアイデアなのですが、測定を利用した方法もあります。(Defect Pair Logical Qubit)

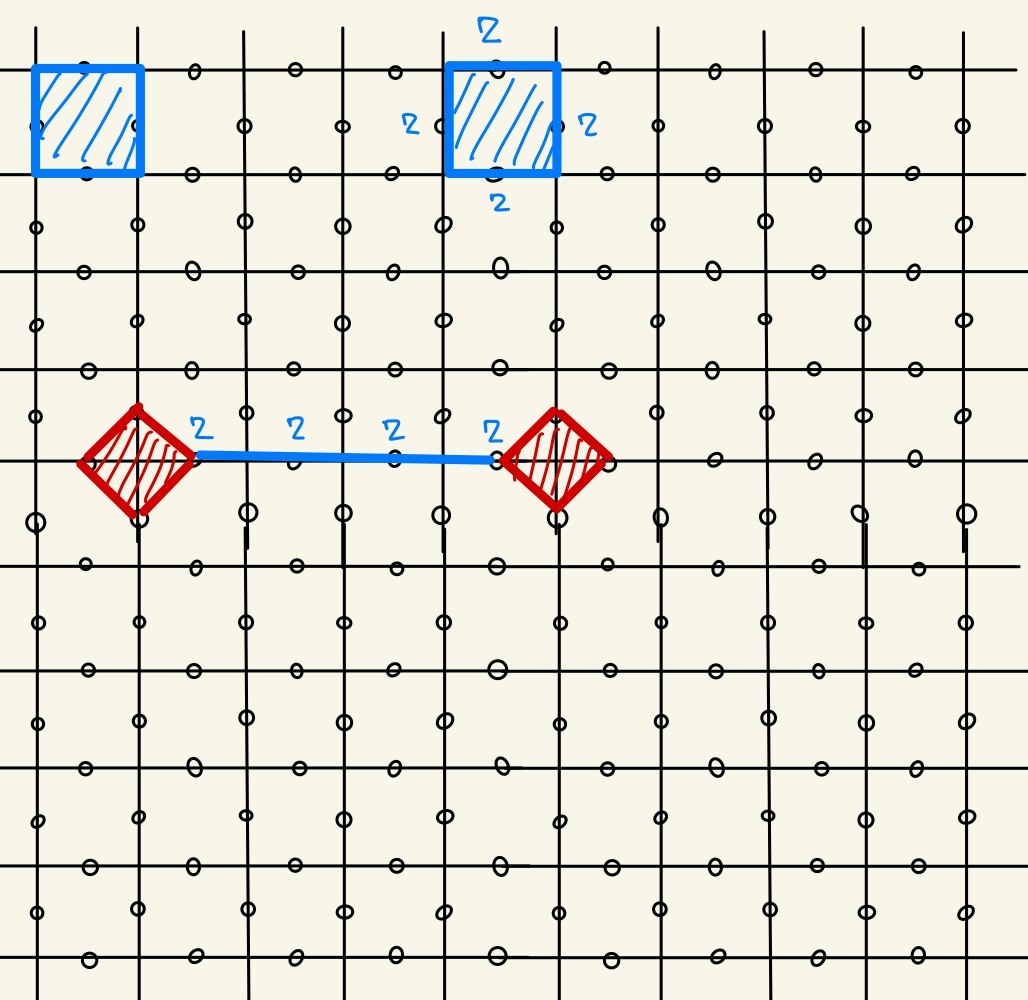
まず、スピン$i$を$x$基底で測定します。これは演算子$X_{i}\otimes I\otimes I\cdots \otimes I$の測定であり、Pauli群の元の測定です。従って5.6 Stabilizer形式での測定の議論が使えて、$i$と辺を共有するPlaquette演算子はStabilizer群から消えます。($X,Z$は反交換)つまり、測定後は

\{\pm X_{i}, \hat{A}, \hat{B}^{*}, B_{1}B_{2} \}

で生成される群がStabilizer群です。($X$の符号は測定結果に応じて定まります)ただし、$\hat{A}$でStar演算子全体を、$\hat{B}^{*}$で消えたPlaquette演算子$B_{1}, B_{2}$以外のPlaquette演算子全体を表します。積$B_{1}B_ {2}$は残ることに注意が必要です。このことを図式的に書くと、下図のstep 1のようになります。斜線部はStabilizerではない部分を表します。

続いて、隣のスピン$j$についても同様に$x$基底で測定します。すると、

\{\pm X_{i}, \pm X_{j}, \hat{A}, \hat{B}^{*}, B_{1}B_{2}B_{3} \}

で生成される群がStabilizer群になります。図式では、Step 2に相当します。さらに、Defectの真ん中のPlaquette演算子を測定します。すると$X_{i}, X_{j}$はStabilizer群から消え、

\{\hat{A}, \hat{B}^{*}, B_{1}B_{2}B_{3}\simeq B_{1}B_{3}\}

で生成される群がStabilizer群になります。(ここで、$\simeq$は演算として同値という意味で使っています。)

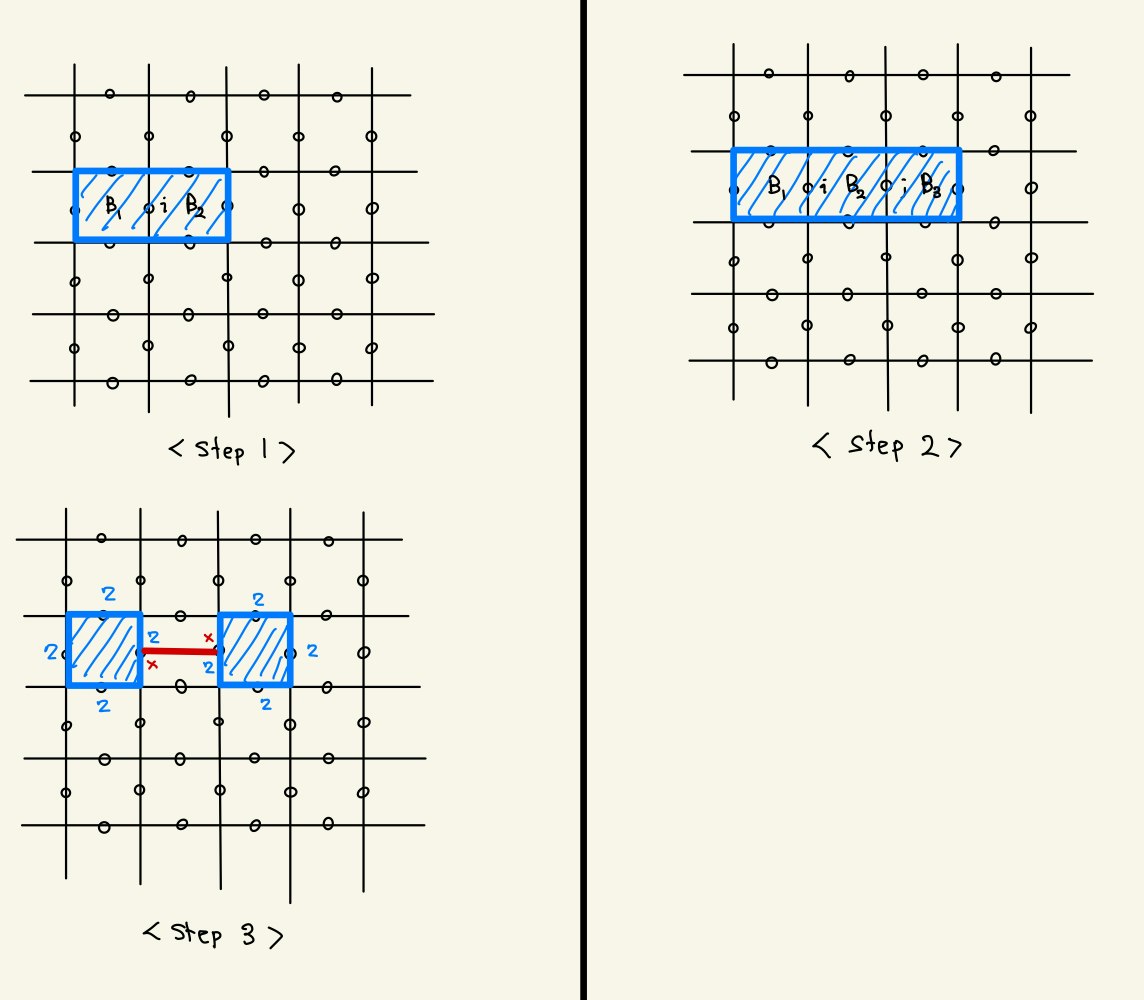
これを見ると、Defectを囲む$Z$Chainが境界を持たず(すなわち全てのStabilizerと交換し)、かつStabilizer群とは独立な演算子になっていることがわかります。すなわち、Stabilizer空間をこの$Z$chainの固有値によって分割することができるので、これはLogical Operatorであるということになります。ただし、$B_{1}B_{3}$もStabilizerなので、二つの$Z$chainのループは、一方のみが独立なLogical Operatorとなります。また、Defect同士を繋ぐ$X$Chainもまた同様に境界を持たず、かつStabilizer群に含まれていないので、Logical　Operatorとなります。また、$X,Z$chainのLogical Operatorをそれぞれ$X_{L}, Z_{L}$とすると、これらの演算子は1点で交わるので反交換します。よって$X_{L}, Z_{L}$はLogicalなPauli$X,Z$とみなせます。こうして、Defectの導入によって新たに1bitのLogical Qubitを作れました。⁹

8. Braiding

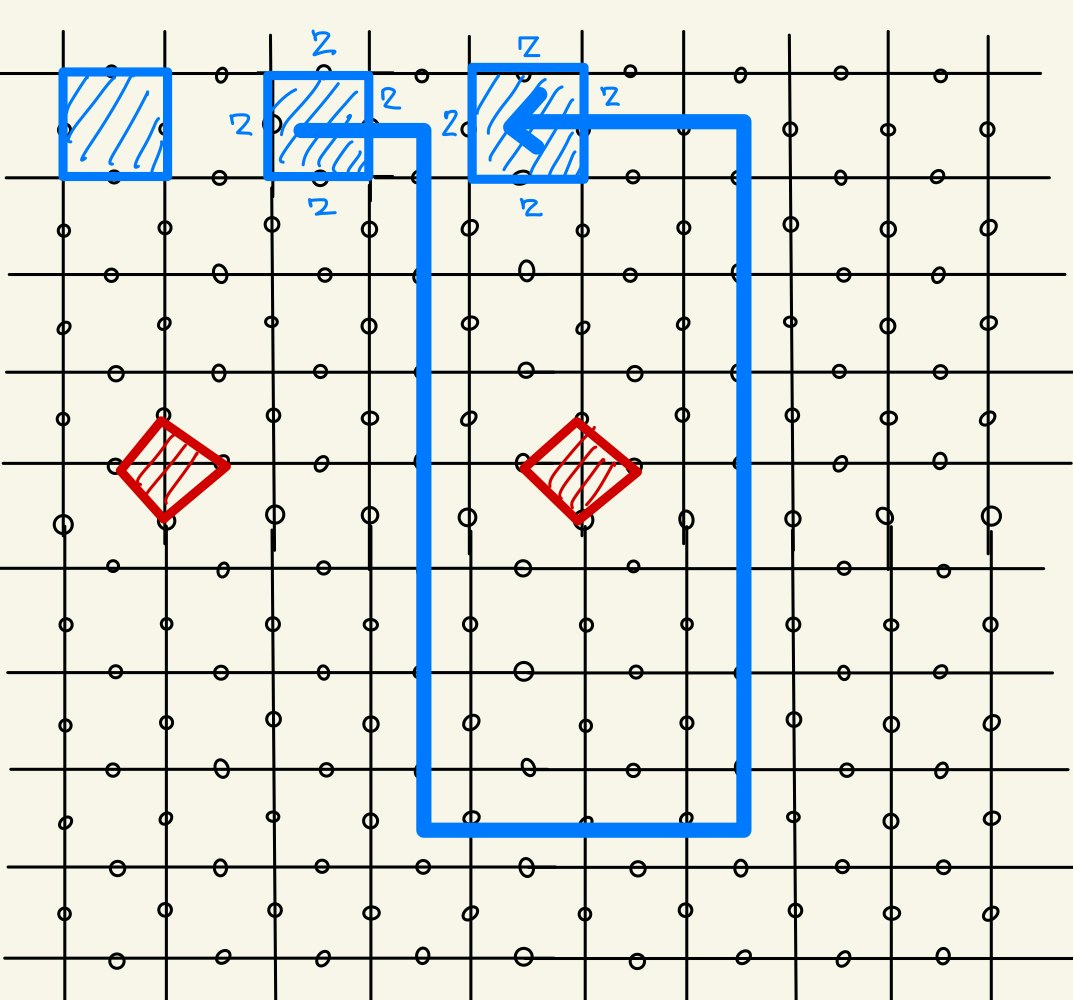
さて、ようやく準備が整ったので、Toric CodeでCNOTゲートがどのように実現されるかみていきましょう。前節の話で$X,Z$を入れ替えても全く同じ話ができることに注意すると、下図のようにDefectを二種類作ることができます。青のDefectは$X$基底で測定してPlaquette演算子をStabilizerから除外したもので、赤のDefectは$X$基底で測定してStar演算子をStabilizerから除外したものです。

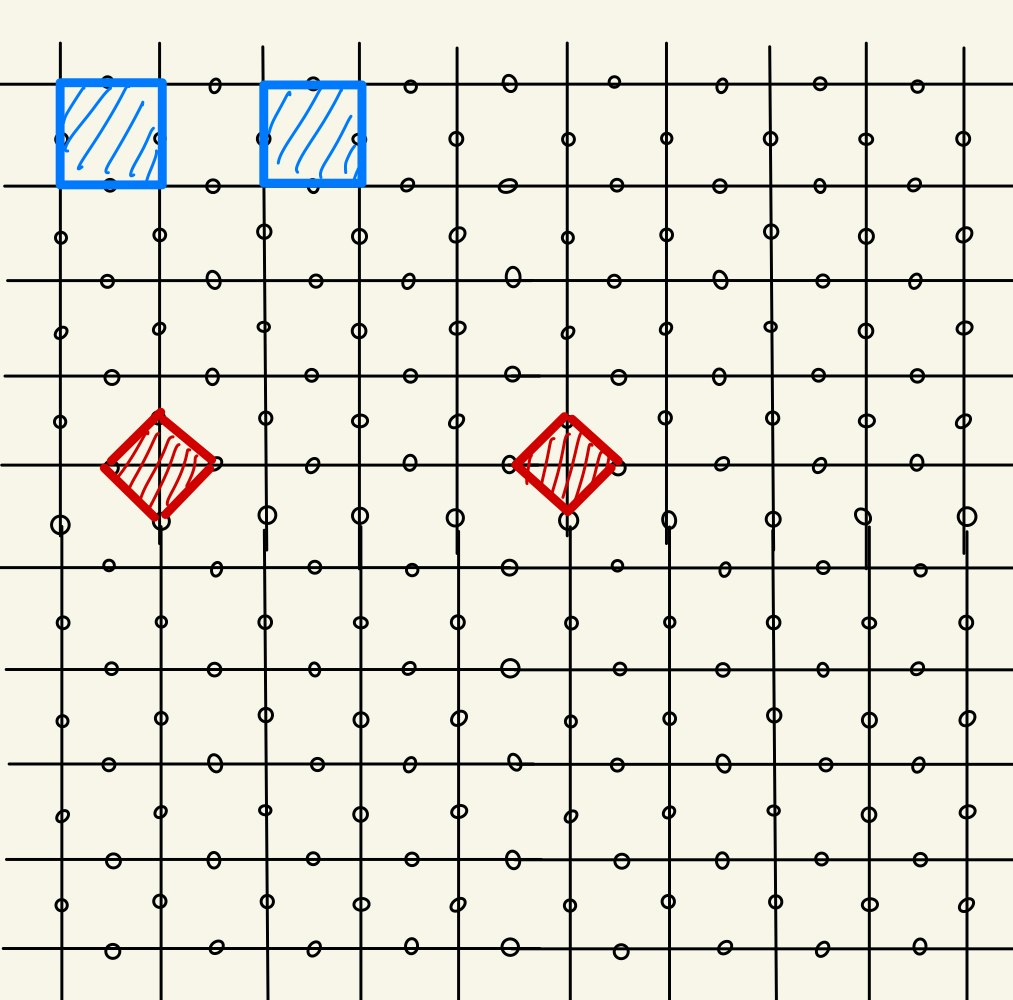
ここで、赤のDefectを取り囲むように、右の青のDefectを動かします(Braiding)。Defectを移動させるには、前節の図のstep2, step3に対応する操作をすればよいです。

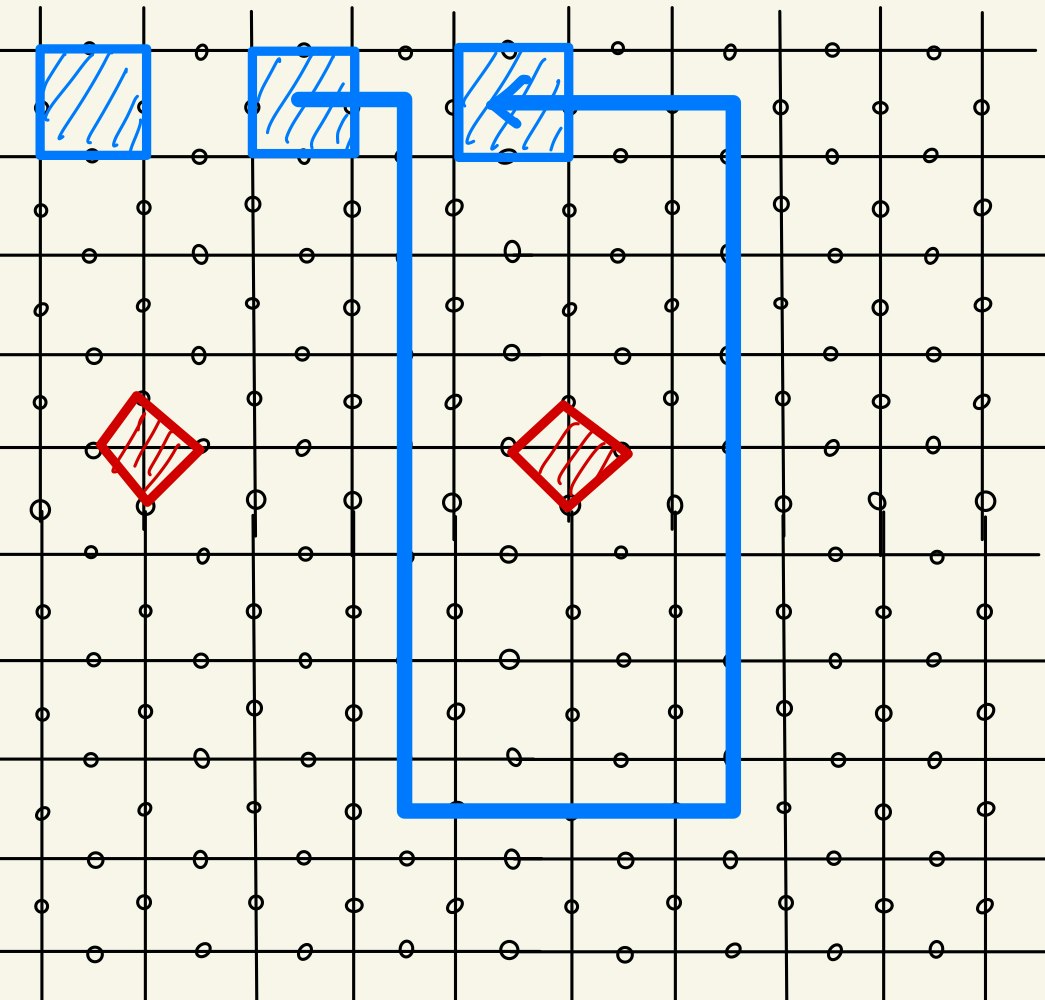
まず初めに、Braidingによって$X_{L}$がどう変化するかを考えます。$X_{L}$の端は常にDefectにつながっているので、Defecｔの移動と共に$X_{L}$もまた一緒に伸び縮みすることに注意します。

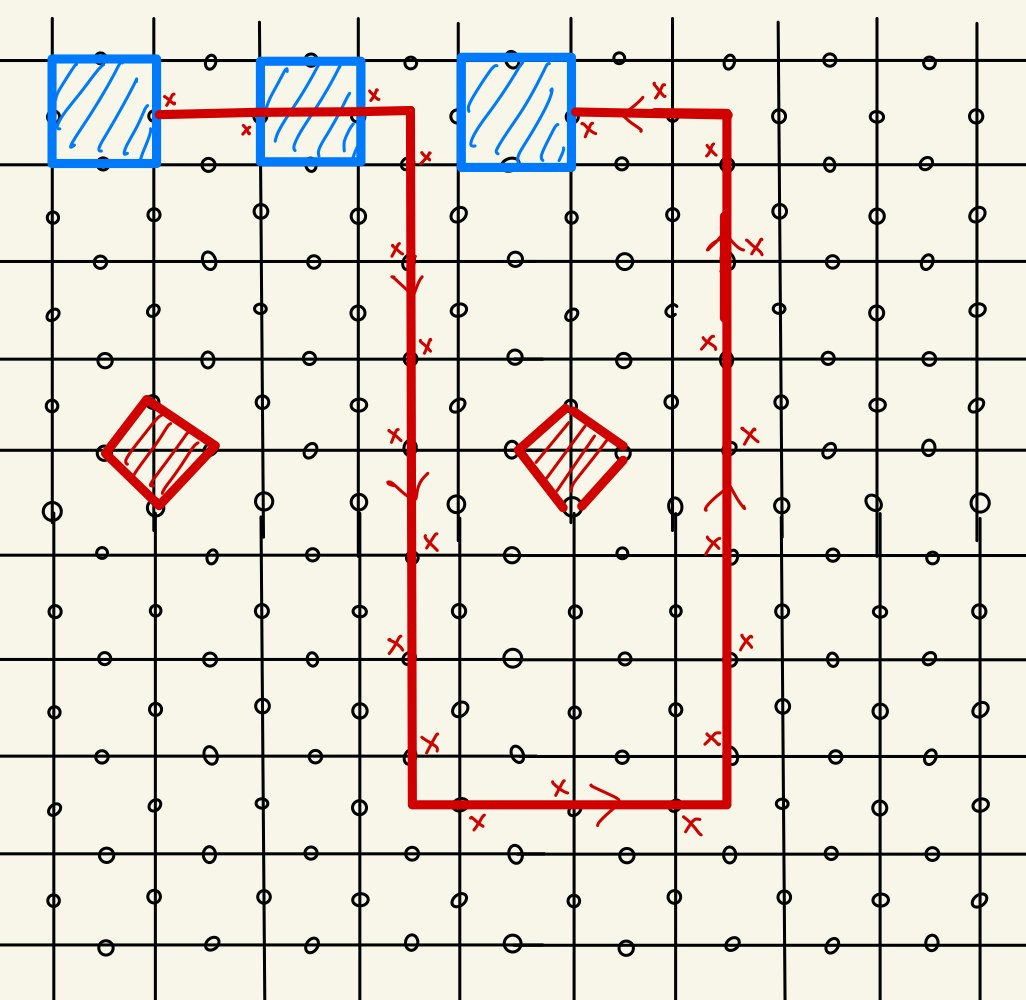
ここで、図のように$X$のループ演算子を作用させます。これはStar演算子の積となっていてStabilizer群に含まれるので、Stabilizer状態に対しては恒等演算子とみなせます。$X_{L}$とループ演算子と被ったところでは$X$が2回かかるのでその部分は消えます。

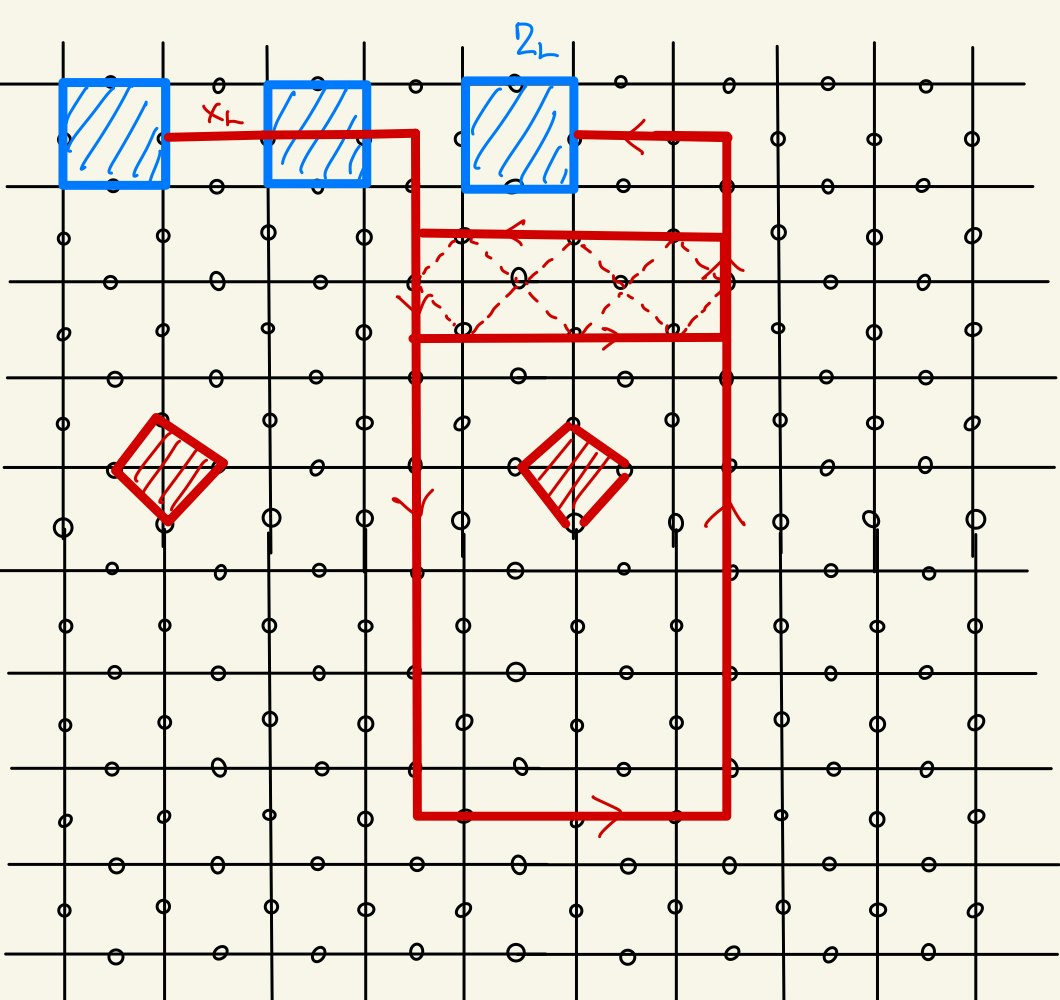
同じ要領で$X$のループ演算子を次々に作用させることで、結局下図のような演算子が残ることになります。

すなわち、

U_{braiding}(X_{L} \otimes I) = X_{L}\otimes X_{L}

がわかります。

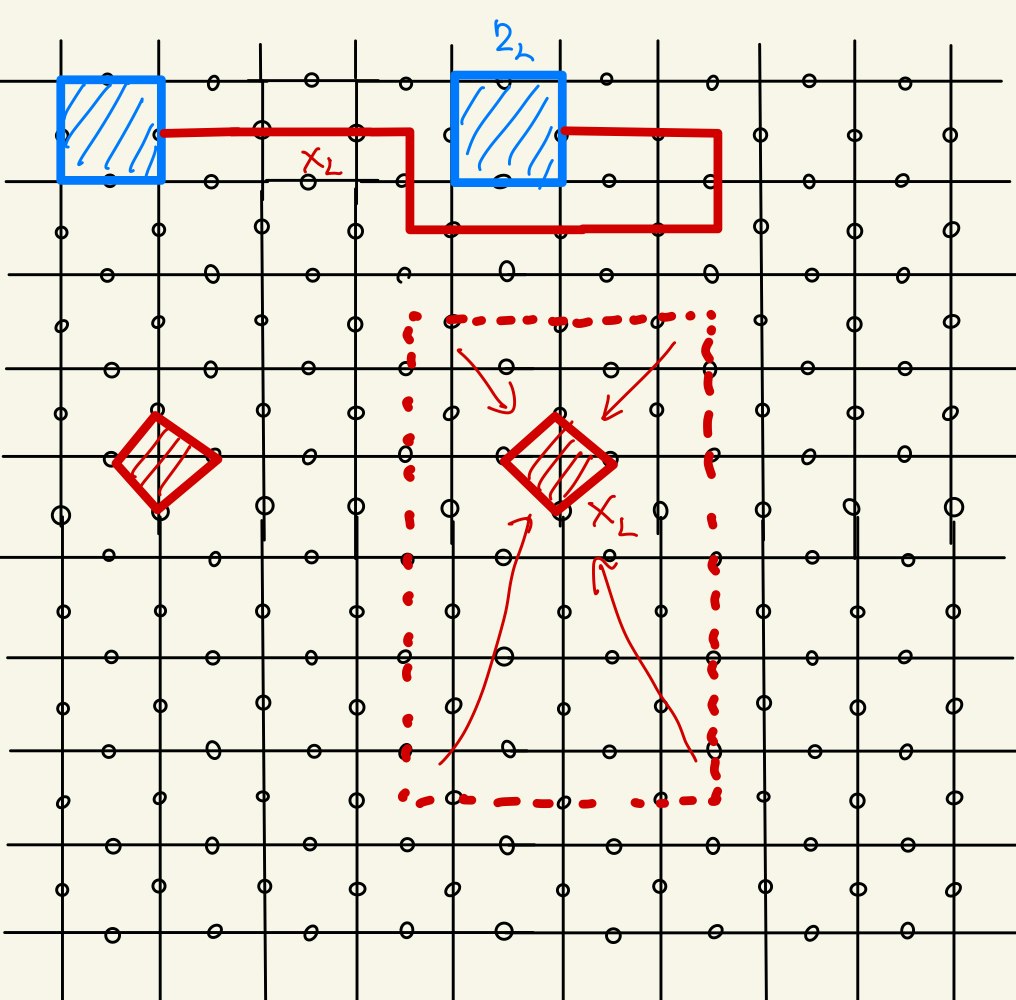
次に、もう一方のDefect Pair Logical Qubitの間の$Z_{L}$がBraidingによってどう変化するかを考えます。
Defectによって$Z_{L}$は下図のように「押しのけられ」て変形します。

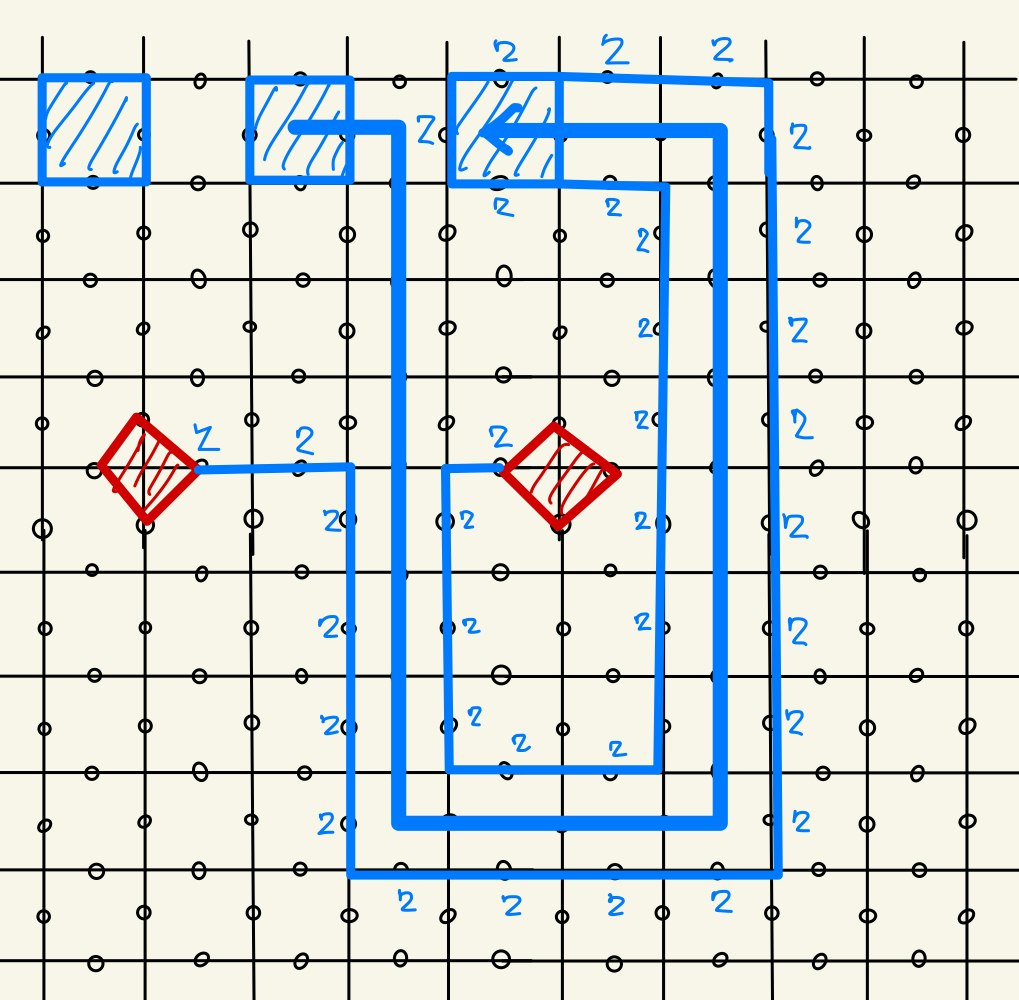
この場合もDefectを取り囲まない自明な$Z$のループ演算子を次々に作用させることで経路を変形できることに注意します。

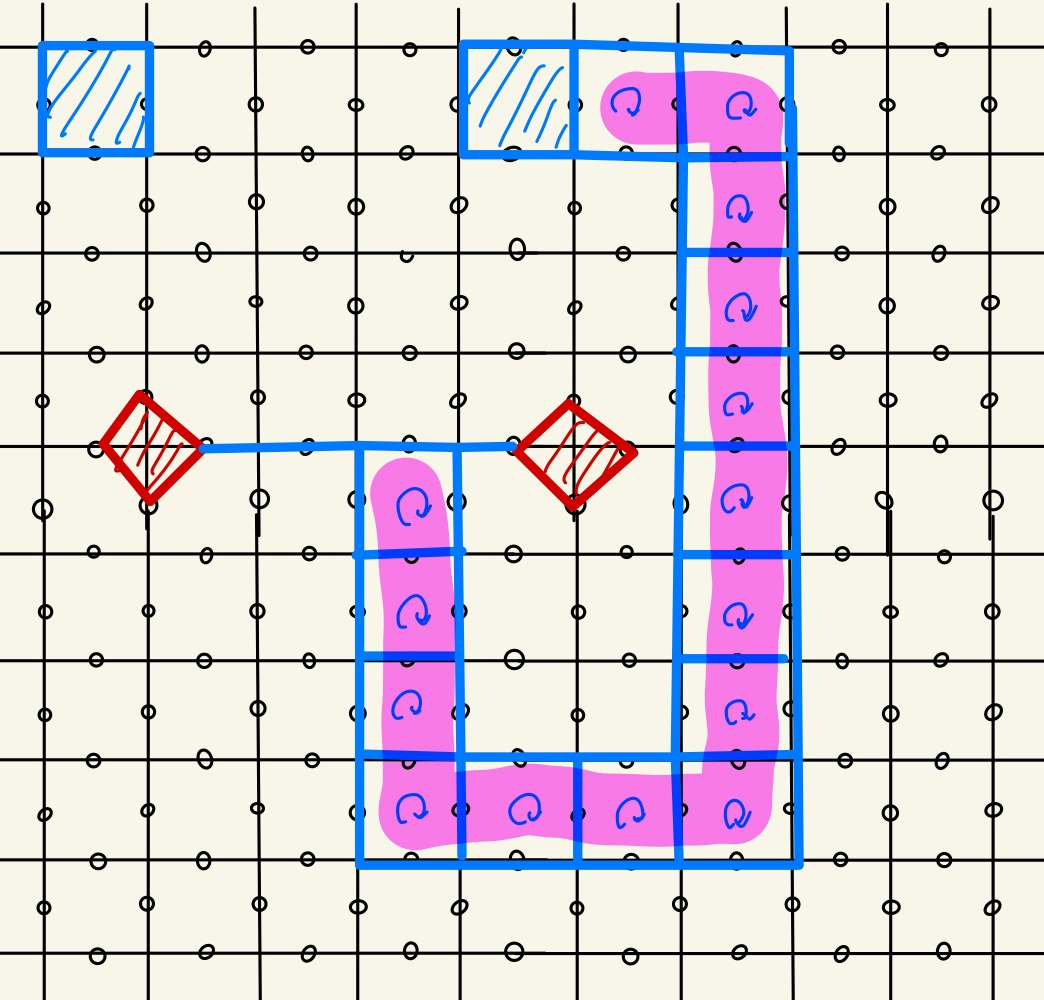
すなわち、

U_{braiding}(I \otimes Z_{L}) = Z_{L}\otimes Z_{L}

です。また、上二つの例に比べるとtrivialな例として下図が挙げられます。

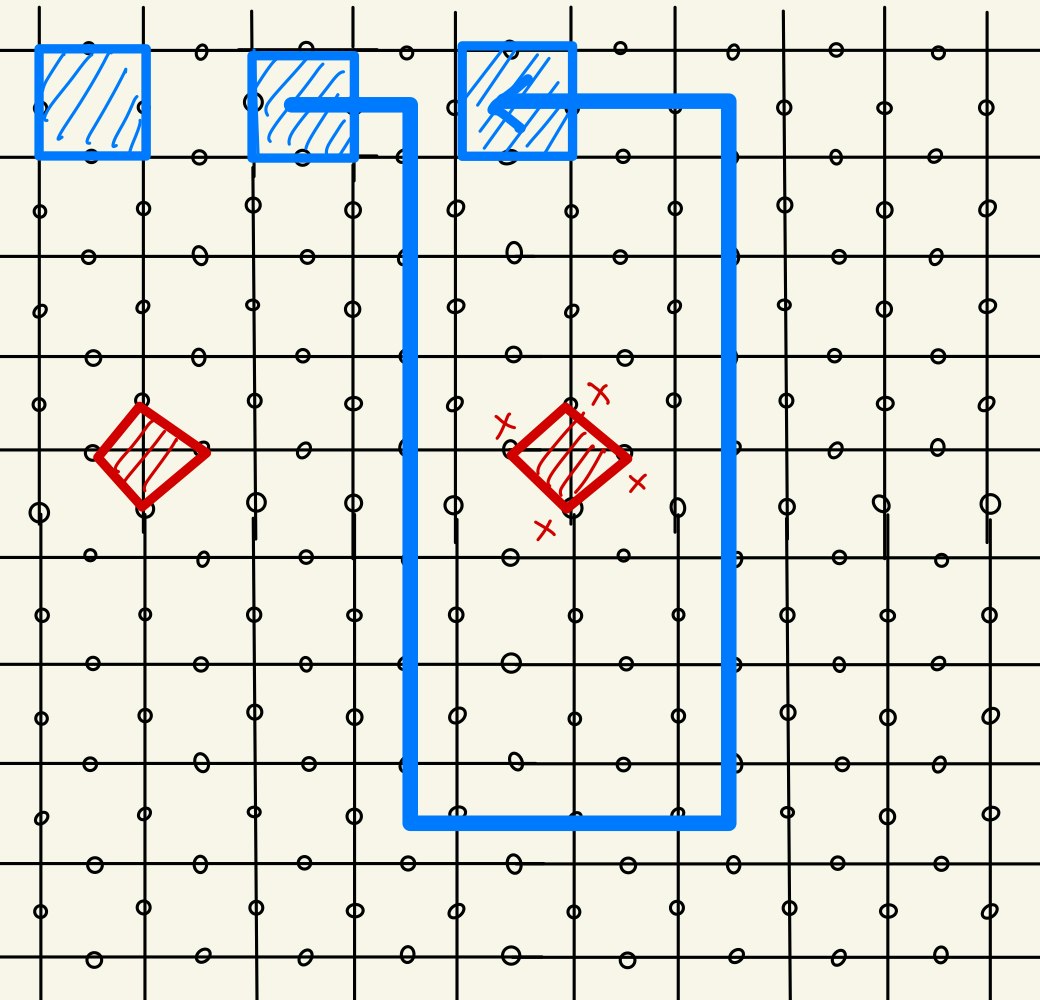
その結果、

U_{braiding}(I \otimes X_{L}) = I \otimes X_{L}\\
U_{braiding}(Z \otimes I_{L}) = Z \otimes I_{L}\\

がわかります。
以上の結果をまとめると、

U_{braiding}(X_{L} \otimes I) = (X_{L}\otimes X_{L})U_{braiding}\\
U_{braiding}(I \otimes Z_{L}) = (Z_{L}\otimes Z_{L})U_{braiding}\\
U_{braiding}(I \otimes X_{L}) = (I \otimes X_{L})U_{braiding}\\
U_{braiding}(Z \otimes I_{L}) = (Z \otimes I_{L})U_{braiding}\\

となります。(ただし、演算子が何もない状態でBraidingを行なっても何も起きない、ということを用いました。)この式を5.7 CNOTゲート再考の表式と見比べると、CNOTゲートとBraidingは同じ操作を表していることがわかります。つまり、CNOTゲートはBraidingで実現できることがわかり、疑問が解決しました。

ここで一連の手順を観察すると、Defectの周りを取り囲んで「絡みつく」ことでループが一点に縮むことができなくなるということがCNOTゲートを実現するために重要だとわかります。そして、2.CNOTゲートで述べたように、CNOTゲートは量子もつれを生成する上で鍵となる操作なのでした。以上のことを踏まえると、量子もつれの「もつれたる所以」がなんとなく腑に落ちたような気がしませんか？

9. おわりに

今回はToric CodeでのCNOTゲートの実現というテーマに絞って記事を書きました。量子力学の初歩からBraidingまで到達しようとしたのは、今思えば無茶だったかもしれません。「ちょっぴり」どころか「うんざりするほど」長い記事になってしまいました。もしこの記事を読んでくれた高校生や駒場生の方がいたとしたら、物理は眠いと勘違いしないことを祈っています。(実際は目が覚めるほど面白いですよ)

また、「大体OK」を多用してラフに書いたため、ガチプロの方々に激怒されないかも心配です。この記事は僕自身の勉強を兼ねて書いたものですし、自分の証明や見方も所々に含まれています。そして、他の人にチェックしてもらったわけではありません。したがって、内容自体の間違いがある可能性は大いにあります。「大体OK」ではないところがあればぜひ教えてください。

~~ガリ勉、変人、宇宙人と思われてしまうので~~普段は一般向けに今回のように長々と話をすることは絶対にありませんが、アドカレを見に来てくださる皆さんに対してであれば、こういう「全力！物理100%」な記事もありかもしれないと思って書きました。最後まで読んでくださった方はありがとうございました。¹⁰

参考文献

Kitaev, A.and Laumann, C. "Topological phases and quantum computation"
https://doi.org/10.48550/arXiv.0904.2771
藤井啓介氏のYouTube：https://www.youtube.com/@user-ib9gg7xd4r
藤井啓介「量子計算超入門」　https://quantphys.org/keisukefujii/tokyotopological.pdf

その他

記事の長さの都合等で今回は触れることができませんでしたが、Toric Codeや関連する話題には他にも色々と面白い性質があります。例えば、励起状態にはフェルミオンともボソンとも異なる統計性をもつ準粒子、エニオンが出現します。また、Toric Codeでは誤り訂正を巧妙なスキームで実現することができます。

自分自身まだまだ勉強し始めたところですので、これから色々と深く学んで行けたら良いなと思います。先輩、後輩、同輩問わずプロの皆さんは、ぜひ色々と教えてください!

Hilbert空間とは$\mathbb{C}$上の完備な計量線型空間のこと。「良い性質を持った線型空間」と思えばそんなに間違っていません。 ↩
この記号はディラックのブラケット記号と呼ばれ、量子状態を表すのによく用いられます。あまり気にしなくて良いです。 ↩
一般には複素数です ↩
厳密にはこの場合$\ket{0},\ket{1}$は直交している必要があります。 ↩
今回の目的のためにはただの平面でも構いませんが、平面の端でのStar演算子やPlaquette演算子の定義が面倒なのでトーラスにしました。 ↩
部分集合であって、それ自身演算について閉じていて群をなすもの ↩
パウリ群の演算子はエルミートか反エルミートです。反エルミートな演算子$\hat{O}$の固有値は純虚数となり、特にPauli群に含まれるものに関しては固有値は$\pm i$となります。よって、$\hat{O}^{2}=-I\in S_{n}$となります。これは定義に反し矛盾となるので、結局エルミートな演算子しかStabilizer群の中には存在しないことがわかります。 ↩
これらはZXXZが1つずつずれた形をしており、可換であることが確かめられます ↩
一連の操作でStabilizer群の生成元の数が1つ減っているので、Stabilizer空間の次元はdefectを作る前の2倍になっていることに気がつきます。これはLogical Qubitの数が1つ増えたことに対応しています。 ↩
今回の記事に書かれている内容の大部分は大阪大学の藤井啓介先生のyoutubeチャンネルやPDFを参考にしました。参考文献にリンクが記されています。大変分かりやすく面白い内容になっていると思うので、興味のある方はぜひご覧ください。藤井先生、ありがとうございました。 ↩

結んで作るCNOTゲート 〜量子もつれとBraiding〜