ABC205 Python3解説(A問題~D問題)

こんにちは、こんばんは。現役緑色コーダーのRuteです。
今回はABC205のA問題からD問題までの解説を行います。

A問題 - kcal

問題文
$100$mLあたり$A$kcalのエネルギーをもつドリンクがあります。このドリンク$B$mLは何kcalのエネルギーを持つでしょうか？

制約

• $ 0 \leq A,B \leq 1000$
• 入力はすべて整数である

出力
答えを表す数値を出力せよ。
なお、想定解答との絶対誤差または相対誤差が$10^{-6}$以下であれば正解として扱われる。

解説

答えは、$\frac{AB}{100}$です。ただ、そのまま計算しようとすると小数誤差が生じる可能性も否定できないのでDecimalとよばれる十進表記ライブラリを使って分数を正確な値で表現しましょう。

ABC205.py

#Decimalライブラリを読み込んでいる
from decimal import Decimal
A,B = map(int,input().split())
print(Decimal(A * B / 100))

B問題 - Permutation Check

問題文
$1$以上$N$以下の整数からなる長さ$N$の数列$A = (A_1,A_2,...A_N)$が与えられます。
$A$が$(1,2,...,N)$の並び替えによって得られるかどうかを判定してください。

制約

• $1 \leq N \leq 10^3$
• $1 \leq A_i \leq N$
• 入力はすべて整数

出力
$A$が$(1,2,...,N)$の並び替えによって得られるならYes.そうでないならNoと出力せよ。

解法1 ソートする

$A$を昇順にソートしてそれが$(1,2,...,N)$の並び替えと同じかを判定する方法です。
計算量はソートの部分が$O(NlogN)$,入力の部分が$O(N)$なので$O(NlogN)$で処理を行うことが可能です。

ABC205B1.py

N = int(input())
A = list(map(int,input().split()))
ls = [i+1 for i in range(N)]
A.sort()
if ls == A:
  print("Yes")
else:
  print("No")

(これは解答例の一部です。最短で2行で解くことも可能です...)

解法2 setの長さで条件分岐

制約が$1 \leq A_i \leq N$であることに着目すると、この問題は以下の問題に言い換えることができます。
「$1$から$N$までの数がすべて存在するか」
すべて存在するかどうかについては$O(N)$で判定することができます。

ABC205B2.py

N = int(input())
A = list(map(int,input().split()))
#setを用いると種類数を管理することができます
B = len(set(A))
if B == N:
  print("Yes")
else:
  print("No")

(これは解答例の一部です。最短で2行で解くことも可能です...)

この問題の類題としては以下の問題が挙げられます。
ABC164 - C問題「gacha」

C問題 - POW

問題文
数$X$を$Y$回掛けたものを「$X$の$Y$乗」といい、$pow(X,Y)$で表します。例えば、$pow(2,3) = 2 × 2 × 2 = 8$です。
$3$つの整数$A,B,C$が与えられるので、$pow(A,C)$と$pow(B,C)$の大小を比較してください。

制約

• 10^9 \leq A,B \leq 10^9
• 1 \leq C \leq 10^9
• 入力はすべて整数

解説

愚直に、${10^9}^{10^9}$などを計算しようとすると、多倍数整数の計算をすることになります。
これでは、残念ながら実行時間制限の2秒以内に処理を行うことはできません。

ここで着目するのは、$C$の偶奇と、$A,B$の符号、さらに$A,B$の絶対値$|A|,|B|$の値です。この値に着目して場合分けをすればよいです。

基礎知識としては

• マイナスの値を2以上の偶数回掛けるとプラスになる
• マイナスの値を奇数回掛けるとマイナスになる
• プラスの値は掛ける回数が正であればプラスになる
• ある整数自身を掛ける回数が0である場合、1になる

ということですね。

この知識に基づいて条件分岐を行うと、$O(1)$で解くことが可能です。

回答コードは長いので、AtCoderの提出リンクを直接貼っておくことにします。

D問題 Kth Excluded

問題文
長さ$N$の正整数列 $A = (A_1, A_2, \dots, A_N)$ と $Q$個のクエリが与えられます。
$i , (1 \leq i \leq Q)$ 番目のクエリでは、正整数 $K_i$ が与えられるので、$A_1, A_2, \dots, A_N$ のいずれとも異なる正整数のうち、小さい方から数えて $K_i$ 番目のものを求めてください。

制約

• $1 \leq N,Q \leq 10^5$
• $1 \leq A_1 < A_2 < \dots < A_N \leq 10^{18} $
• $1 \leq K_i \leq 10^{18}$
• 入力はすべて整数である。

出力
$Q$出力せよ。$i$行目には$i$番目のクエリに対する答えを出力せよ。

解説

1.最初に思いつきやすい解法

まず、$1$から$10^{18}$までの数字の配列を作成します。これを$B$とします。
$2$番目の制約から任意の$i,j$に対して $A_i \leq A_j$が成り立つので、
各$A_i$を配列から除外していきます。
あとは、各$K_i$に対してB[K_i-1]を求めます。

...残念ながら、この解法は間違っています
まず、Pythonにおいて、配列から値を削除するremoveは配列の長さを$N$とすると、$O(N)$の計算量を要します。これを$N$回行うので$O(N^2)$となります。
配列の長さが$(10^{18})$なので、実行時間制限の3秒以内に間に合いません。
また、そもそもの話、長さ$10^{18}$の配列を作成しようとすると、配列の長さ分の計算量がかかるので、配列を作成しようとする時点でTLE(実行時間制限超過)となってしまいます。

では、除外せずに、$K_i$番目の値を求める方法とは、どのような方法なのでしょうか？

2.ステップ1

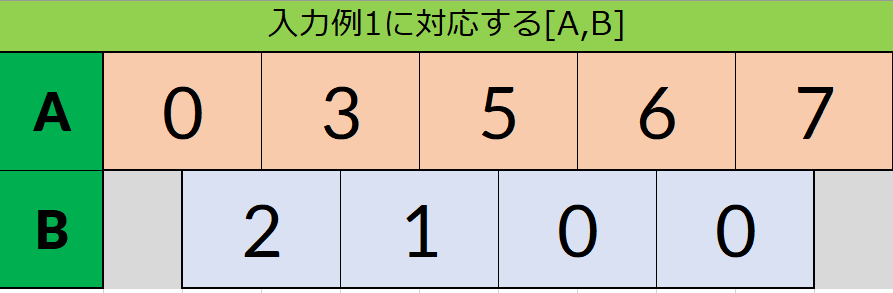
まずは、入力例1をもとに、各区間における以下の数を考えます。
(ここでは、配列を1-indexedで考えます)
各$i$ $(1 \leq i \leq N)$について

• $i = 1$のとき、$0$から$A[1]$までの間にある正整数の場合の数
• $2 \leq i \leq N-1$のとき$A[i-1]$から$A[i]$までの間にある正整数の場合の数
• $i = N$のとき、$A[N]$からあとにある正整数の場合の数

この場合の数を並べた数列を$B$とします。

• $B[1] = A[1] - 1$
• $B[2]$から$B[N]$ $= B[i] - B[i-1] - 1$

となります。$B[N+1]$は定義しようとすると$\inf$になるので定義していません。

3.ステップ2

次に、$B$に対しての累積和をとります。
累積和というのは、元の数列の0項目からからある項までの総和として定義される数列です。
今回の場合、累積和を$C$とすると、以下のようになります。

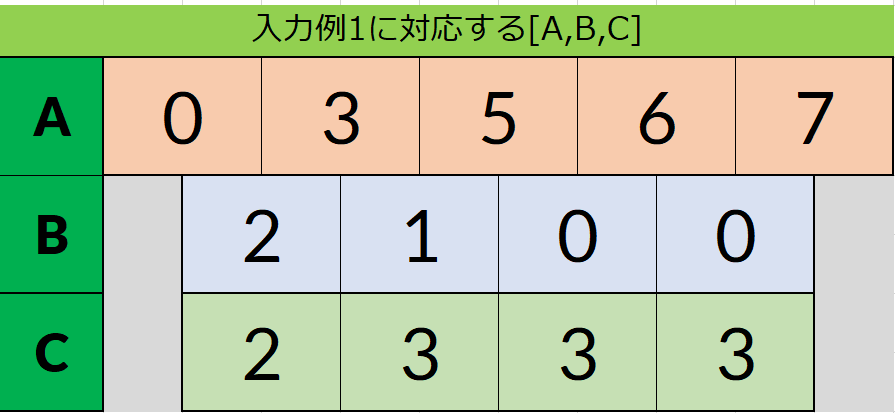
この累積和を求めることにより、各$C[i]$について
$C[i]$ = 0から$A[i+1]$までの正整数の中で
($A_1,A_2,...A_{i+1}$)に含まれていない正整数の場合の数

というように求めることができました。

3.ステップ3

これで前準備は完了です。あとは、
$A_1, A_2, \dots, A_N$ のいずれとも異なる正整数のうち、小さい方から数えて $K_i$ 番目のものを求める

ということを考えます。

これまでに考えた数列のうち、$C$に着目すると、
各$i$ $(1 \leq i \leq Q)$について
$K_i \leq C[j]$ となる最小のインデックス$j$を求める。すると
$A[j]$から$A[j+1]$の間に小さい方から$K_i$番目の数が含まれる

ということが分かります。

そして、求めたインデックス$j$の値によって、答えは以下のようになることがわかります。

答え

(jは1-indexedではなく0-indexedであることに注意してください)
$j = 0$の場合は0から$A[1]$の間に$K_i$番目の数があります。
この場合の答えは$K_i$になります。
$1 \leq j \leq N-1$の場合$A[j]$から$A[j+1]$までの間に$K_i$番目の数があります。
この場合の答えは$A[j] + (K_i - A[j])$となります。
$j = N$の場合は$K_i$番目の数は$A[N]より大きいことがわかります。
したがって、この場合の答えは$A[N] + (K_i - A[N])$となります。

したがって、最小のインデックスを求めればよいですが、これにも罠があります。

例えば、$Q$回のクエリにおいて$K_i$を受け取って、最小のインデックスを左から線形探索で求める、という解法ではどうでしょう？

一見この解法でも解けそうに見えますが、例えば最小のインデックスがすべて$N$だった場合、最小のインデックスを1個ずつ調べていくのに$O(N)$の計算量が必要で、かつこれを$Q$回繰り返すので計算量は$O(NQ)$となります。

今回の制約についてもう一度着目すると、
制約

• $1 \leq N,Q \leq 10^5$
• $1 \leq A_1 < A_2 < \dots < A_N \leq 10^{18} $
• $1 \leq K_i \leq 10^{18}$

$N,Q$が$10^5$以下なので、最大で$10^{10}$回程度の計算が必要になります。
高速な言語でも1秒間に$10^8$回程度の計算が精一杯なので、これでは実行時間制限の3秒以内に間に合わず、TLEとなってしまいます。

ステップ4

では、高速に探索するためにはどのような方法を考えればよいでしょうか。

これまでに考えた数列のうち、$C$に着目すると、
各$i$ $(1 \leq i \leq Q)$について
$K_i \leq C[j]$ となる最小のインデックス$j$を求める。すると
$A[j]$から$A[j+1]$の間に小さい方から$K_i$番目の数が含まれる

最小のインデックスを求めるということを考えると、二分探索が探索回数を減らすのに有効なのではないか？と考えられそうです。

したがって、二分探索によって最小のインデックスを求めることにより、

• 毎回の二分探索の計算量が$O(logN)$,
• 二分探索を$Q$回実行するので二分探索部分の計算量が$O(QlogN)$,
• 前処理部分の計算量は$O(N)$

ということから$O(N + QlogN)$の計算量でこの問題を解くことができました。

解答例を示します。

ABC204D.py

#bisectは二分探索のライブラリです。
import bisect
import copy
N,Q = map(int,input().split())
#端点を追加するために[0]を入力に加えています
A = [0] + list(map(int,input().split()))
B = []
#Bの計算
for i in range(N):
    B.append(A[i+1]-A[i]-1)
#元の配列に影響を与えないようにコピーをしています
C = copy.deepcopy(B)
#累積和の計算部分
for i in range(len(C)):
    if i > 0:
        C[i] += C[i-1]
for i in range(Q):
    K = int(input())
    #K ≦C[j]となる最小のインデックスjを求めています。
    j = bisect.bisect_left(C,K)
    if j == 0:
        print(K)
    elif j == N:
        print(A[-1]+(K-C[-1]))
    else:
        print(A[j]+(K-C[j-1]))

以上で、ABC205のA問題~D問題の解説を終了します。
記事に関して質問等がありましたらコメントをお願いします。