自主学習まとめ. 自分にわかりやすく...
[番号]は文末に引用元を表記. 番号が振られていない引用は全体を通して参照.
間違ってる可能性も...
0. イントロダクション -分類問題
機械学習を大別すると分類問題と数値問題に分けられる. そこでこの記事の目的はパーセプトロンから2クラスの分類問題のアルゴリズムを整理することである.
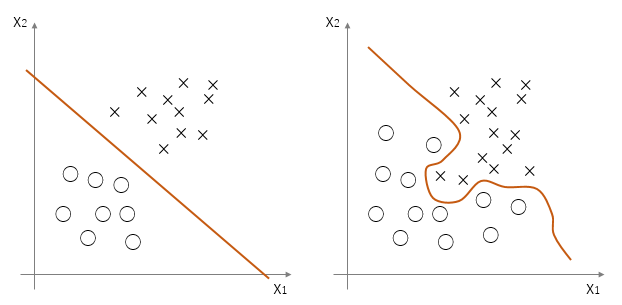
人間の脳細胞ニューロンをまね, コンピューター上で最初に表したものがパーセプトロン(perceptron)である. データを2つのクラスに線形で分離するために考案された. それゆえ非線形問題は解決できず, そのために多層パーセプトロンとSVMのモデルが別々に考案された. 線形問題と非線形問題の分類についてここで取り上げるアルゴリズムでの分類可否を図1に示した.
図1 (左)線形問題:パーセプトロン, ADALINE, 多層パーセプトロン, SVMで分類可能 (右)非線形問題:多層パーセプトロンやSVMでのみ分類可能
また, パーセプトロン, 多層パーセプトロン, SVMの領域の違いについて図2に示した. パーセプトロンのアイデアをもとに, ニューラルネットワークとSVMの各分野が発展した.
ここではパーセプトロンを中心にして, 基本事項をまとめる.
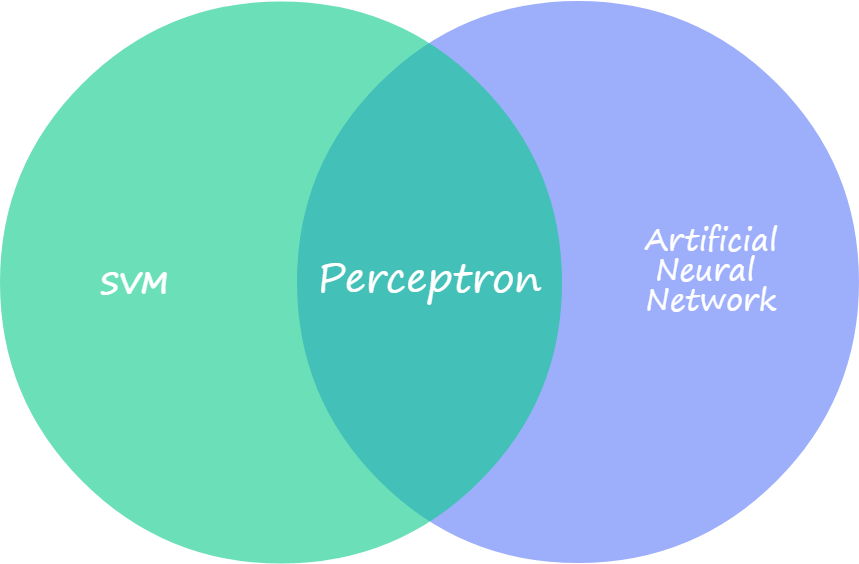
図2 パーセプトロン, ニューラルネットワーク, SVMの関係.
1. パーセプトロン
1957年にローゼンブラット(Rosenblatt)によって考案されたアルゴリズムがパーセプトロンである.
1.1 数学的背景
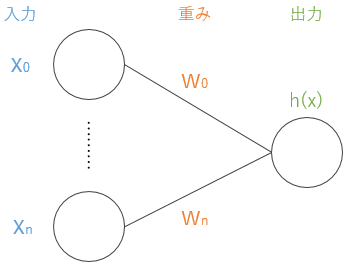
パーセプトロンを数式で表すと次のように書ける. ここで$ \boldsymbol{x} $は入力, $h(x)$は出力, $\boldsymbol{w}$は重み, $ b $はバイアスを表し, 最終的な出力値を出す関数$h(x)$はhypothesis関数と呼ばれる.
\begin{align}
h_w (x) & = w_1x_1+w_2x_2 + b \tag{1}\\
\end{align}
これを一般化し, ベクトルで計算しやすいようにバイアスも入力値$\boldsymbol{x}$の変数とすると, $x_0=1, w_0=b$と書ける.
\begin{align}
h_w (x) & = w_0+w_1x_1+\cdots +w_nx_n\\
&= \sum_{i=0}^n w_ix_i\\
&=\boldsymbol{w}^T\boldsymbol{x} \tag{2}\\
\end{align}
図3 パーセプトロン h=w^Tx
入力データ$\boldsymbol{x}$と重み$\boldsymbol{w}$の乗法の結果がある閾値$\theta$を超えた場合は1, それ以外は-1に分類する. このようにどちらに分類するか決める関数を活性化関数(activation function) $g(x)$といい, パーセプトロンでは活性化関数$g(x)$は一つしかないので, 活性化関数$g(x)$=hypothesis関数 $h(x)$となる. この場合, 活性化関数は$g(x)$は単純なステップ関数 (unit step function)であり, ヘビサイド関数 (Heaviside step function)とも呼ばれる. ここで簡単のため$z=\boldsymbol{w}^T\boldsymbol{x} $とすると
g(z) = \left\{
\begin{array}{ll}
1 & (z \geq \theta) \\
-1 & (z \lt \theta)
\end{array}
\right.\tag{3}
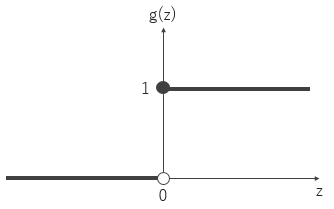
式(3)を簡単にするため, $\theta=0$, $w_0=-\theta$, $x_0=1$とすると式(4)である (図4).
\begin{align}
g(z) &= \left\{
\begin{array}{ll}
1 & (z \geq 1) \\
0 & (z \lt 0)
\end{array}
\right.\tag{4}
\end{align}
パーセプトロンとは活性化関数$g$によって線形分離可能なデータ点を分類するアルゴリズムであり, 重み$\boldsymbol{w}$ですべてが決まる. そのため重み$\boldsymbol{w}$を適切に決定する必要がある. ほかの分類アルゴリズムと区別する際に活性化関数がキーワードとなるため, パーセプトロンは活性化関数にステップ関数を用いたアルゴリズムであるということをここで強調しておく.
1.1 アルゴリズム
学習アルゴリズムは次のステップで表すことができる.
- 重み$w$を0か小さな乱数で初期化する
- それぞれのトレーニングサンプルに対し
2. 出力値$\hat{y}$を計算する
3. 重み$w$を更新する
重みの更新の各iteration $\tau$は次のように書ける.
\begin{align}
\qquad & w_j^{\tau +1}=w_j^\tau +\Delta w_j^{\tau}\\
\Leftrightarrow &\quad w_j:=w_j+\Delta w_j\tag{5}
\end{align}
ここで$\Delta w$は正解の分類$y$, 予測された分類結果$\hat{y}$, 学習率 $\eta , (0\leq \eta \leq 1$)を用いて,
\Delta w_j=\eta (y^i - \hat{y}^i)x_j^i\tag{6}
また, このアルゴリズムは実質重みがかかる層は1層であるため (図1), 単層(単純)パーセプトロンとも呼ぶ.
1.2 論理演算の識別器
パーセプトロンの学習によってandやorなどの論理演算の役割を果たす識別器を作ることを考える. True=1, False=0としいずれかを入力すると, 論理演算をしてくれるパーセプトロンを通過した後に0か1が出力される識別器である. 0か1の出力のため, 式(3)の活性化関数$g(a)$で表すことができ,
これは図5に示したようにAND, OR, NANDの論理を用いた分類は論理演算だけの簡単なプログラムで表すことができる. XOR演算子を用いた分類に関しては多層パーセプトロンの節で言及する.
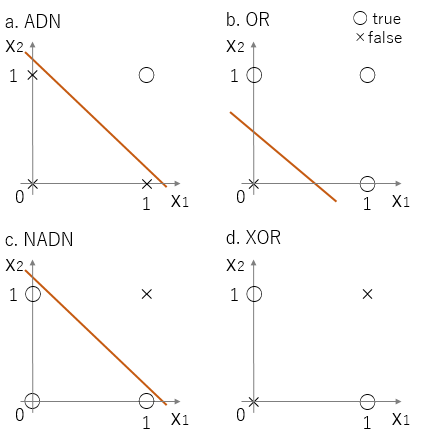
図5 論理結果と分類 a: AND演算子の場合 b: OR演算子の場合 c: NAND演算子の場合 d: XOR演算子の場合. a-cは線形分離できるがdは線形分離できない.
2. ADALINE
パーセプトロンを改良したモデルにADALINE (adaptive linear neuron)がある. Window-Hoff学習ルールとも呼ばれ, パーセプトロンの発表された数年後に発表された. 図6にパーセプトロンとADALINEのアルゴリズムを示した.

図6 パーセプトロンとADALINEのアルゴリズム (出典:'What is the difference between a Perceptron, Adaline, and neural network model?' Sebastianrashka)
また, パーセプトロンとの相違点について表1にまとめた.
表1 パーセプトロンとADALINEの相違点
| パーセプトロン | ADALINE | |
|---|---|---|
| 活性化関数 | ステップ関数 | ステップ関数 |
| 出力 | クラスラベル(離散値) | 連続した予測値 |
| 重みの学習 | - | コスト関数 |
2.1 コスト関数(cost function)
教師あり機械学習において, 学習過程で最適化する目的関数 (objective function)の定義をすることがある. この目的関数の一種にコスト関数 (cost function) $J$がある. ここでのコスト関数$J$を予測されるクラスラベル (target label)と計算結果の誤差の平方和と定義する. ここで, $m$はデータ数である.
J(w)=\frac{1}{2}\sum_{i=1}^m(\hat{y}^i-y^i)^2=\frac{1}{2}\sum_{i=1}^m(h_w(x^i)-y^i)^2\tag{7}
コスト関数$J$は式(7)から明らかなように, 微分可能な凸関数である. そのため, 勾配降下法(gradient decent)を用いて, コスト関数$J$を最小化する重み$w$を計算することができる.
初期の重み$w$とし, 繰り返し計算すると式(5)は次のように書ける.
w_j:=w_j+\eta \frac{\partial }{\partial w_j} J(w_j)\tag{8}
式(8)のコスト関数の偏微分$\partial J/\partial w_j$を計算すると,
\frac{\partial J(w_j)}{\partial w_j} = (h_w(x)-y)x_j\tag{9}
ゆえに, 収束するまで更新される重み$w$は次式となる.
w_j:=w_j+\eta \sum_{i=1}^{m}(h_w(x^i)-y^i)x_j^i\tag{10}
この手法は1ステップごとに極小値に近づき, 偏微分の結果が0に近づく, 即ち接線の傾きがゆるやかになる. トレーニングセットのすべてのサンプルに基づいて, 重みが計算されるため, バッチ勾配降下法(batch gradient descent)と呼ばれる. 極小値に近づくスピードは, 傾きと学習率$\eta$の関係で決まるため, 標準化などで最適な学習率$\eta$を見つける必要がある. 極小値を見つける方法には様々なアルゴリズムがあり, 最急降下法とニュートン法を用いた最適化にまとめた.
3. 多層パーセプトロン (multi-layered perceptron, MLP)
非線形問題を扱うために, 1986年ラメルハート(Rumelhart)によって考案されたのが, パーセプトロンを複数つなぎ合わせ入力と出力以外に隠れた層を持つ多層パーセプトロンである. これも教師あり学習(supervised learning)であるが, 誤差逆伝搬(backpropagation, BP)を導入することで, 効率よく重みの調整ができるようになった. 多層フィードフォワードネットワーク (multi-layer feedforward neural network)とも呼ばれる. パーセプトロンの組み合わせであるため, 図1や図5(d)で示した非線形分離も可能になった.
ところでパーセプトロンを重ねても非連続の非線形モデルとなり, 多層パーセプトロンはロジスティック回帰 (logistic regression)を重ねた連続した非線形モデルであるため, 不適切な名前であるという意見もある$^1$. 詳細の説明に入る前に, パーセプトロンとの相違点を表2にまとめた. また多層パーセプトロンイメージを図7にまとめた. パーセプトロンと異なり$h=\sum g$であることに注意したい.
表2 パーセプトロンとADALINEと多層パーセプトロンの相違点
| パーセプトロン | ADALINE | 多層パーセプトロン | |
|---|---|---|---|
| 活性化関数 | ステップ関数 | ステップ関数 | シグモイド関数など |
| 出力 | クラスラベル(離散値) | 連続した予測値 | 連続した予測値 |
| 重みの学習 | - | コスト関数 | コスト関数 |
| 層 | 単層 | 単層 | 多層 |
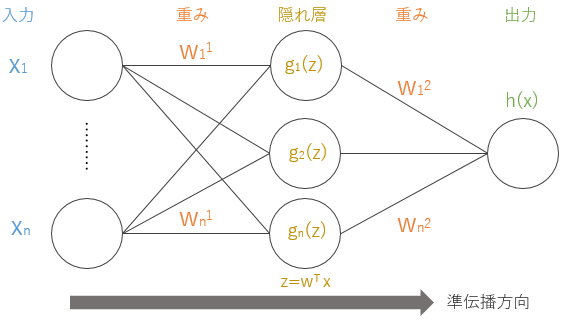
図7 多層パーセプトロン, パーセプトロンの各層がつながり多層となっている.
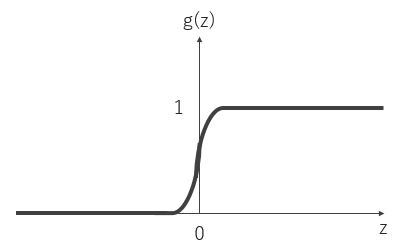
多層パーセプトロンの活性化関数$g$のシグモイド関数 (sigmoid function)であり, 次のように表せる.
\begin{align}
g(\boldsymbol{w}^T\boldsymbol{x})&=\frac{1}{1+exp(-\boldsymbol{w}^T\boldsymbol{x})}\tag{7}\\
g(z)&=\frac{1}{1+e^{-z}}
\end{align}
シグモイド関数はステップ関数と異なり微分可能な関数である.
即ち, 多層パーセプトロンは活性化関数に, シグモイド関数を用いたアルゴリズムである. またニューラルネットワークというと, この多層パーセプトロンを指すことが多い. ニューラルネットワークの活性化関数として, ここで取り上げたシグモイド関数が長年用いられていたが, 近年はReLU関数やPReLU関数を用いられることが多い. また多分類の場合はtanh関数が使われる. これに関してはのちほどまとめたい.
4. サポートベクターマシン (Support Vector Machine, SVM)
1963年に線形識別のためにSVMが発表され, 1992年にカーネル(kernel SVM)を用いた非線形識別の可能性が示唆された. そののち1995年にC CortesとV Vapnikによって論文として発表された. 多層パーセプトロンとは異なる方向に拡張したパーセプトロンの拡張理論である. 大域最適解を求められることから, ニューラルネットワークを用いた分類より強力な分類アルゴリズムであることも多い (図9).
SVMでの最適化の目的は, データ間のギャップであるマージンの最大化である.
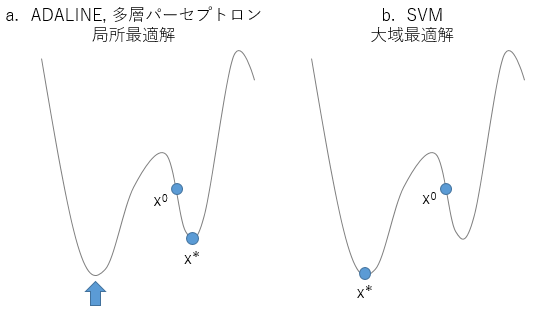
図9 初期値$x_0$, 収束解$x^*$とした. a: ADALINEや多層パーセプトロン, ニューラルネットワークの解. 初期値$x_0$を与えた谷に落ちていくため, この初期値$x_0$では矢印の解には到達できない. そのため適切な初期値を与える必要がある. b: 初期値$x_0$がどの地点であれ, 収束解$x^*$は大局最適解となる.
SVMについての詳細は別途ページを作成する予定である. ここではSVMの特徴となるカーネルとヒンジ関数についてのみ取り上げる.
4.1 カーネルSVM
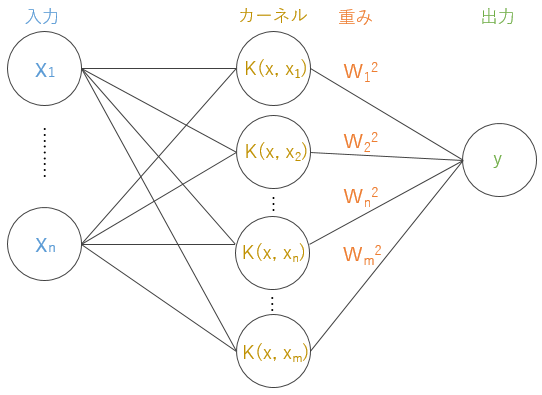
線形分離不可能なデータ$x^i$を非線形写像$\phi$で, もとの次元よりも高い次元に変換することで線形分離可能にする. この際に高次特徴空間での内積計算$K(x_i, x_j)$が必要となり, これをカーネル関数$K$という. カーネル関数さえわかれば非線形写像$\phi$を明示的に求める必要がなくこれをカーネルトリックという. サポートベクター以外のカーネル関数の重みが0となることで高次元だが計算量も少なくて済む. 図10にSVMの模式図を示した.
4.2 論理演算の識別器
図5(d)のXOR問題はカーネル関数を用いると図11のようになる. 数学的な照明は割愛した.(詳細は[2]を参照)
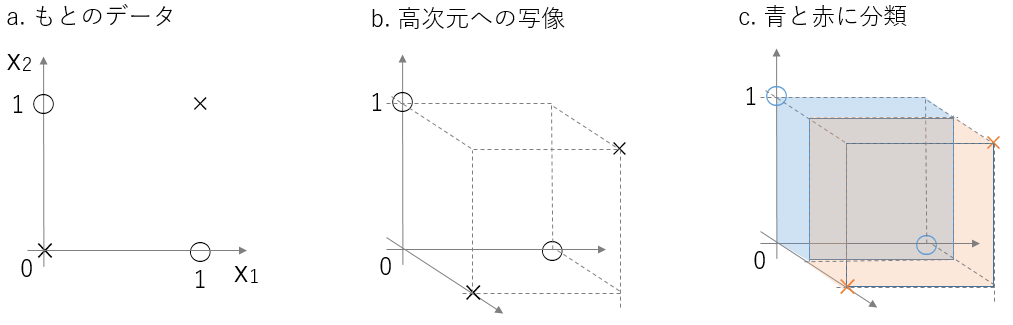
図11 平面を高次元に写像するときのイメージ a: 入力値と分類 b: 高次元に変換した結果 c: 高次元上で線形素子で分類した様子
4.3 最適化する関数
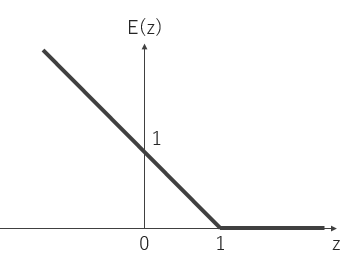
損失関数としてヒンジ(損失)関数(hinge function)を用いる. ヒンジ関数とは変数$z$がある定数より大きいか小さいとき0で一定となり, それ以外では線形に増加または減少するような関数である. 特に$a$が正なら$a$をそうでなければ0を出力する関数を$[a]_+$と表記する. SVMでのヒンジ関数は次のように定義される.
E_{SV}(z)=[1-z]_+\tag{8}
SVMの損失関数はヒンジ関数に正則化項を追加したものである.
l=\lambda ||w||^2+[1-z]_+\tag{9}
この節の主旨は, パーセプトロンからSVMがどのように発展したのかであるため, これ以上の詳細については踏み込まない.
まとめ
線形識別器であるパーセプトロンを中心に, 活性化関数を改良したADALINE, 層を増やすことで非線形識別器となった多層パーセプトロンが生まれた. またパーセプトロンの理論をベースに, データ間のマージンを最大にして分類する手法としてSVMが生まれた. そこからさらに入力データを高次元写像にすることで非線形問題を線形問題として扱うことが可能なカーネルSVMが生まれた. いずれの理論も, 凸関数であるコスト関数や損失関数の極小値を求めることで最適解が求められることが共通している. ここで取り上げた識別器の相違を表3にまとめた.
表3 識別器間の相違
| パーセプトロン | ADALINE | 多層パーセプトロン | SVM | |
|---|---|---|---|---|
| 活性化関数 | ステップ関数 | ステップ関数 | シグモイド関数など | SVM損失関数 |
| 出力 | クラスラベル(離散値) | 連続した予測値 | 連続した予測値 | 離散値 |
| 重みを学習する関数 | - | コスト関数 | コスト関数 | 損失関数 |
| 層 | 単層 | 単層 | 多層 | 単層 |
Reference
[1] C. M. Bishop. Pattern Recognition and Machine Learning. Springer, 2006
[2] V. Cherkassk and F. M. Mulier. Learning from Data: Concept, Theory and Methods, IEEE John Wiley & Sons, 1998
Python機械学習プログラミング
ゼロから作るDeep Learning
A. Geron. Hands-On Machine Learning with Scikit-Learn & TensorFlow. O'Reilly Media, 2017
S. Raschka et al. Deeper Insights into Machine Learning. Packt, 2016
http://www.asimovinstitute.org/neural-network-zoo/
https://www.microsoft.com/en-us/research/wp-content/uploads/2012/01/tricks-2012.pdf
https://see.stanford.edu/materials/aimlcs229/cs229-notes1.pdf