はじめに
統計や機械学習を学ぶとき、最初の方にベイズの定理を学ぶ事が多いです。
ただ、このベイズの定理の利点がいまいちイメージしにくかったので、今回、記事にまとめました。
ベイズの定理については知ったけど、そのありがたみがいまいちよく分からないが対象読者となると思います。
ベイズの定理について
ベイズの定理は、事前確率と事後確率の関係を表す式で、
事象$A$,$B$が起こる確率を$P(A)$,$P(B)$で表し、
事象$A$の観測後に事象$B$が起こる条件付き確率(事後確率)を$P(B|A)$で表す時、
事象$B$の観測後に事象$A$が起こる条件付き確率$P(A|B)$について以下の式が成り立ちます。
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
その導出方法や詳細な説明については、以下の様なサイトで分かり易く解説されているかと思います。
参考サイト
・ベイズの定理とベイズ更新
・ベイズの定理の基本的な解説
式だけみるとなんてことはないのですが、とにかくここで重要な事は、$P(A|B)$を$P(B|A)$,$P(A)$,$P(B)$で求める事が出来る点であることを頭に留めておいて頂きたいです。
クラス分類における例
例えば、あるデータ$x_i$がクラス$w_1$,$w_2$に属するかどうかを求めるとします。
これは、データ$x_i$が観測された際、それがクラス$w_1$にある確率$P(w_1|x_i)$と、クラス$w_2$にある確率$P(w_2|x_i)$
を比べる事で、どちらのクラスに属するかを求められます。
\left\{
\begin{array}{ll}
P(w_1|x_i) > P(w_2|x_i) ⇒ x_i \in w_1 \\
P(w_1|x_i) < P(w_2|x_i) ⇒ x_i \in w_2
\end{array}
\right.
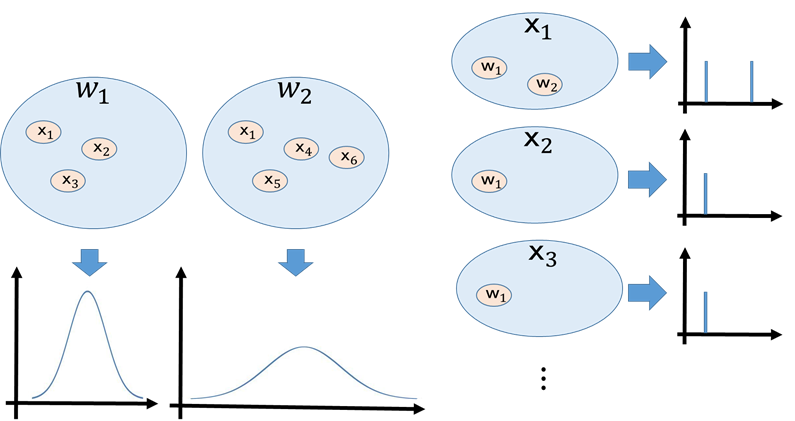
しかし、$P(w_j|x_i)$を直接求めようとすると、取りうるデータ全てに対して、事後確率$P(w_j|x_i)$を求める必要があり、これは現実的には、データ数が限られているので膨大なデータが必要となります。(下図の右のイメージ)
一方、事前確率$P(x_i|w_j)$を求める場合は、有限のデータからでもそのデータの分布から有る程度信頼できる値を取り出すことが出来ます。
よって、統計的に識別問題を解く際には、直接求められない事後確率を事前確率から求められるベイズの定理が有効になります。(下図の左のイメージ)
おわりに
今回は、ベイズの定理の有用性について、説明させて頂きました。
この定理が機械学習などの分野において、どのように使われているのか、少しでもイメージを持つきっかけになればと思います。
最後まで読んでいただきありがとうございました。