修論に追われながらですが、気分転換にやってみたので記事にしてみます。
実際に実装してみるとscipyでSVMを実装している人が少なく、わりとはまることが多かったので知見をシェアしてみます。
この記事はサポートベクターマシンという本をベースにしています。この本は間違いが多いのでもし読むなら注意して読むようにしてください。個人的にはあまりおすすめはできません。
※1 サポートベクターマシンについて十分知識があるという前提で話します。ご注意ください。
※2 もっと良いソースの書き方があればぜひ教えてください。
線形サポートベクターマシンを最適化問題に落とす
SVMの双対問題
$x_i$と$y_i$は、それぞれ$x_i = (x_i^{(1)}, \dots, x_i^{(d)}) \in \mathbb{R}^d$, $y_i \in \{ -1, +1 \}$となり、$x$は特徴データで、$y$は正解データを指しています。$\alpha = (\alpha_1 , \dots, \alpha_l)^{\mathrm{T}}$は識別超平面を求めるために使うラグランジュ関数のラグランジュ定数とします。
このときSVMの識別超平面$w^{\mathrm{T}}x+b=0$最適化問題の双対問題を考えます。双対問題は、以下のようになります。
$\alpha$について最大化すべき目的関数は
\sum_{i=1}^l\alpha_i - \frac{1}{2}\sum_{i,j=1}^l\alpha_i\alpha_jy_iy_jx_i^{\mathrm{T}}x_j
で、その制約条件は、
\alpha_i \ge 0,\quad i = 1, \dots, l
\sum_{i=1}^l{\alpha_iy_i} = 0
となります。
最適化問題の定式化
これをscipy.optimize.minimizeにあるように、最適化問題の定式に落とし込んでいきます。慣習に習って$g \ge 0$を不等式制約、$h = 0$を等式制約としておきます。
\begin{align}
f(\alpha) &= \sum_{i=1}^l\alpha_i - \frac{1}{2}\sum_{i,j=1}^l\alpha_i\alpha_jy_iy_jx_i^{\mathrm{T}}x_j \\
g_i(\alpha_i) &= \alpha_i \ge 0, \quad i = 1, \dots, l \\
h(\alpha) &= \sum_{i=1}^l{\alpha_iy_i} = 0
\end{align}
scipy.optimize.minimizeに解かせる
scipy.optimize.minimizeの説明
scipy.optimize.minimize(以下minimize)の使い方をこの記事で使う必要最低限で簡単に紹介します。
from scipy.optimize import minimize
cons = [{"type": "ineq", "fun": g}]
res = minimize(fun, x0, method="SLSQP", constraints=cons)
minimizeの引数funは先程紹介した$f(\alpha)$に対応しています。ここに最適化してほしい式を返すような関数を指定します。
x0は初期値です。SVMを扱っている場合では凸最適化問題なのであまり気にせず零ベクトルnp.zeros()でも入れてあげましょう。
methodはこの最適化問題のソルバー(=minimize)にどのような解放で最適化問題を解いてもらうかを指定します。僕はあまり最適化の知識がないので、とりあえず"SLSQP"(=Sequential Least SQuares Programming(逐次二次計画法))を選んでみました。
constraintsは制約を指定するdictまたはdictのシーケンスです。シーケンスというのはリストまたはタプルなどと思っておけばいいです。
dictは、辞書型で"type"キーに制約の種類(不等式制約、等式制約)を入れ、"fun"キーにその制約を表す関数をいれておきます。これもminimizeのfunと同様にすればよいです。
目的関数、制約条件の関数化
今回はクロージャを使って作成していますが、本来ならばminimizeのargsパラメータなどでどうにかできそうです。
※minimizeの仕様上、目的関数を最小化するようになっているため、最大化する目的関数の符号を逆転させることで実現しています。
# 目的関数
# x, yはデータで、データを指定して関数を実行すると引数が$\alpha$の関数が返ってくるのでそれを`minimize`に使わせる。
def get_obj(x, y):
def obj(alpha):
second = np.array([alpha[i]*alpha[j]*y[i]*y[j]*np.dot(x[i], x[j]) \
for i in range(len(alpha)) for j in range(len(alpha))])
return - np.sum(alpha) + .5 * np.sum(second)
return obj
# 不等式制約(制約の数だけ作れるようにしていることに注意)
def get_g(i):
def g(alpha):
return alpha[i]
return g
# 等式制約
def get_h(y):
def h(alpha):
return np.sum([alpha[i]*y[i] for i in range(len(alpha))])
return h
constraintsの値を作成
不等式制約の数だけ関数を作成していることに注意してください。
cons = [
{'type': 'eq', 'fun': get_h(y)} # 等式制約
]
for i in range(len(x)):
cons.append({'type': 'ineq', 'fun': get_g(i)}) # 不等式制約
最適化問題を解いて、識別超平面を得る
さきほど使ったものをそれぞれminimizeに入れて使います。
# 学習データの作成
ONE_DATA = 30
x = np.vstack((np.random.normal(loc=-2, scale=1.0, size=(ONE_DATA, 2)),\
np.random.normal(loc=2, scale=1.0, size=(ONE_DATA, 2))))
y = np.hstack((np.repeat(-1, ONE_DATA), np.repeat(1, ONE_DATA)))
# ソルバーの実行
res = minimize(get_obj(x, y), np.zeros(len(x)), constraints=cons, method="SLSQP")
minimizeが返すresというものは、最適化の実行結果の詳細を持つオブジェクトになっています。print(res)するとこうなります。
fun: -0.13412273818124631
jac: array([ 2.82717060e-01, 3.85807756e-01, 3.13518258e-01,
2.77660560e-01, 4.86643452e-01, 4.78479423e-01,
4.67139196e-01, 5.05073734e-01, 2.60325832e-01,
# 省略
8.17233417e-01, 2.69528620e-01, 3.99119448e-01,
6.87747058e-01, 5.80251390e-01, 6.86778139e-01,
0.00000000e+00])
message: 'Optimization terminated successfully.'
nfev: 313
nit: 5
njev: 5
status: 0
success: True
x: array([ -4.05360147e-16, 9.85552613e-16, -2.03652689e-16,
3.49785386e-16, 6.35631441e-16, -1.85546533e-16,
9.43039335e-17, -1.77270683e-16, -5.21819014e-16,
# 省略
-3.01016448e-16, -2.69363170e-17, 7.08757201e-17,
6.82412540e-16, 9.35886104e-17, -6.49034939e-17])
res.xがこの最適化問題の解になります。これがminimizeが出した最適な$\alpha$ということになります。
主問題から
w = \sum_{i=1}^l\alpha_iy_ix_i
が成り立つので、得られた$\alpha$を代入することで最終的な識別境界の式が得られます。
このソルバーの性質上、0になるべきところでも完全に0にならないため、非常に小さい数字tol未満のものはこちらで0と置き換えてしまいます。このしきい値が小さすぎるとサポートベクトルの選定に失敗します。
lpha_hat = res.x
tol = 1e-10
support_index = np.where(alpha_hat > tol)[0]
non_suppoert_index = np.where(alpha_hat <= tol)[0]
alpha_hat[non_suppoert_index] = 0
# ここでalphaからパラメータの計算
w = np.sum([alpha_hat[i]*y[i]*x[i] for i in range(len(x))], axis=0)
最後に、バイアスであるbを計算します。
# ラベルが-1のサポートベクトルを選出
x_m = x[support_index][np.where(y[support_index]==-1)]
# ラベルが+1のサポートベクトルを選出
x_p = x[support_index][np.where(y[support_index]==1)]
# サポートベクトルを一つだけ採用してbを計算
b = - ( np.dot(w, x_p[0]) + np.dot(w, x_m[0]) ) / 2
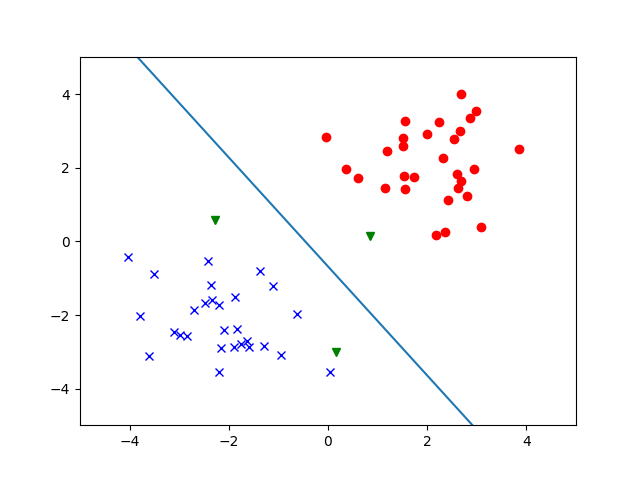
そして、図示をして終了です。
# 二次元の識別超平面=直線のyに関する式を計算
def classifier(w1, w2, b, x):
return -w1/w2*x - b/w2
# データ点の描画
for xi, yi in zip(x, y):
# サポートベクトルの描画
# 条件としてはモレがあるが、ほぼモレは起こりえないのでこのまま。
if (xi[0] in x_m and xi[1] in x_m) or \
(xi[0] in x_p and xi[1] in x_p):
plt.plot(xi[0], xi[1], 'gv')
continue
# ラベルごとに記号を分ける
if yi == 1:
plt.plot(xi[0], xi[1], 'ro')
else:
plt.plot(xi[0], xi[1], 'bx')
x = np.linspace(-5, 5, 100)
y = classifier(w[0], w[1], b, x)
plt.plot(x, y)
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.show()
試しに線形分離が不可能な場合でこれを実行してみると、プログラムが終了しなくなります。主問題の制約条件が成立する候補がなくなってしまうからでしょうか。
ちなみに今回はあえて双対問題でやってみましたが、主問題でやっても同じような結果が得られるかと思います。
これから趣味でやったことで調べてもあまり情報がないものは日記にしておこうかなという思いでやってみましたがなかなか楽しかったです。
研究のやる気が戻ってきたので、それではまた。