はじめに
最近ディープラーニングが盛り上がっていますね。その中でもディープラーニングをはじめとする機械学習に出てくるような本を読んでいるとよく出てくるsoftmax関数
y_i = \frac{e^{x_i}}{\sum_{j=1}^N e^{x_j}}
があります。最近本を読んでいたらこいつが登場し、そろそろちゃんと理解しようと思ったのでその考察をシェアします。
本題
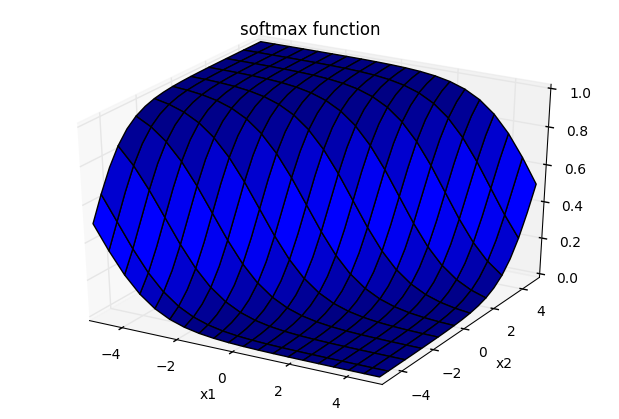
結論からいうと、softmax関数を3Dグラフにプロットするとこうなります。
(実際、この結果が見たくてググったがなかなかヒットせず)
これは$x_1, x_2$の値がともに$[-5, 5]$である状況で$i=2$に関するsoftmax関数
y_2 = \frac{e^{x_2}}{e^{x_1} + e^{x_2}}
の挙動をプロットしたものになります。このグラフを観察するとわかることが2点あります。これから個別に見ていきます。
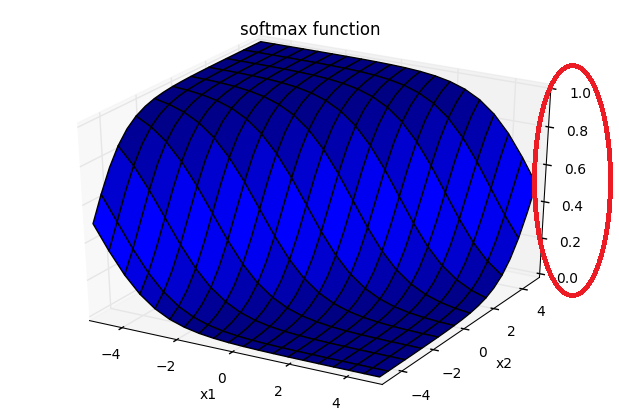
値域(関数の取りうる値)が0から1の間である
これがよくsoftmax関数の利点として挙げられていることです。もちろん数学的に示すことも可能です。この点ではsigmoid関数と親戚関係であることが言えます。
(実際、sigmoid関数の多クラスへの拡張という表現がされています。)
この特徴のおかげで真偽の判断を確率的なあいまい性を残した状態で扱いたいときに大変有効になります。
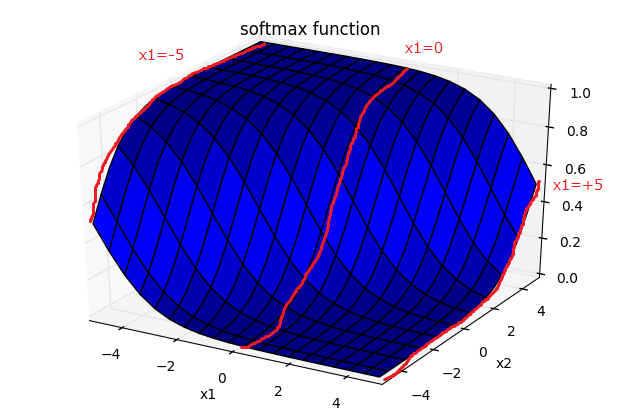
maxのような挙動をしている
これも重要な性質ですが、$x_1$に比べて相対的に$x_2$の値が大きいときに大きな値をとるようになっています。
$x_1=-5$のとき、すなわち他の値が$x_2$に対して小さいときは、$y_2$は大きな値を取りやすくなっています。反対に、$x_1=+5$のとき、すなわち、他の値が$x_2$に対して大きいときは、$y_2$は大きな値が取りにくくなっています。
言い換えれば、「自身$x_j$が他の要素$x_{k(\ne j)}$よりも目立っている確率」のような感覚でとらえることができます。
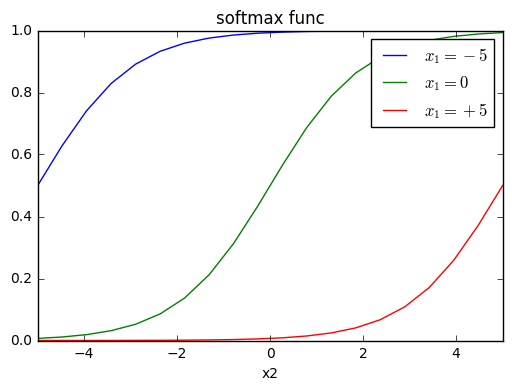
この現象を比較しやすいよう、それぞれの$x_1$の値ごとにプロットしてみます。
ちなみに蛇足ですが、$x_1 = 0$のときは
y_2 = \frac{e^{x_2}}{1 + e^{x_2}}
より、
y_2 = \frac{1}{1 + e^{-x_2}}
となり、sigmoid関数が得られます。
この理解を直感的に多次元に拡張するならば、「softmax関数は多くの次元からなる入力のうち、自分の値が他の値たちに比べて一番目立っているならば、その値が$1$に近づく関数である」といえます。
終わりに
いかがでしたか。
ポイントとしては、この関数が他の入力値に相対的に反応するというところでしょうか。
この記事が少しでもsoftmax関数の直感的な理解につながれば幸いです。
※余裕があれば多次元の場合での可視化についてもやってみます。