はじめに

ロボットをやっている人なら一度は聞いたことあると言って過言じゃない（過言かも）PythonRoboticsですが、
このPythonRobotics中の自己位置推定(Localization)プログラムにEnsemble Kalman Filter(EnKF、アンサンブルカルマンフィルタ)が無かったので、勉強がてらEnKFを実装しました。

PythonRoboticsとは

PythonRoboticsはロボットアルゴリズム用のPythonで書かれたOpen Source Softwareであり、自己位置推定・経路計画・制御などのサンプルコードがあります。
現在Githubのstar数はほぼ6000starで、これはロボティクスタグで世界3位、個人リポで世界1位だそうです。スゴイ。
リポジトリ
https://github.com/AtsushiSakai/PythonRobotics
ドキュメント
https://pythonrobotics.readthedocs.io/en/latest/index.html

詳しくはメインコントリビューターであるsakai atushi@Atsushi_twiさんが以前勉強会で発表したスライドがあるので、興味があれば参照ください。
https://docs.google.com/presentation/d/1QhcGvjxO_zBzwIKxZYbsmWFkct_h7eXDrZ82JqsGVYg/edit#slide=id.gc6f73a04f_0_0

Ensemble Kalman Filterとは

Ensemble Kalman Filterは気象予測の分野で考案されたカルマンフィルタの派生アルゴリズムで、最近はシステム制御でも使われるようになりました¹。
アルゴリズムの詳細は以下の記事を見てください。EnKFの利点・欠点や他の非線形カルマンフィルタについても書いてあります。
Ensemble Kalman Filterを用いた非線形システムの推定

上の記事にあるように、EnKFはParticle Filter(PF)と比べると精度は高くないですが, 少ない粒子数で状態を表せるので計算が軽いです。
EnKFはアルゴリズムの中で状態量の推定誤差共分散行列の計算を必要としないので，状態ベクトルの次元が大きい時により効果的になります¹．~~(この記述書いてて思ったんですが，プログラムをランドマーク位置も推定するSLAMで実装した方が良かった気がしました．やりませんが)~~

アルゴリズムの導出は片山先生の『非線形カルマンフィルタ』¹を参照ください。

プログラムの内容

プログラムではロボットがホイールオドメトリとジャイロによって入力値を，
ランドマーク位置を既知としてランドマークまでの距離を観測値として取得し，
それらをEnKFで統合します．

プログラムは以下のプログラムと『非線形カルマンフィルタ』¹を参考に書きました。
PythonRobotics Particle Filter

具体的な設定は以下です。

状態量
$\mathbf{x}=[x \quad y \quad \theta \quad v]^T$
$x$：$x$方向のロボット位置、$y$:$y$方向のロボット位置、
$\theta$：ロボットの方位角,$v$：ロボットの速度
観測量
$\mathbf{z_j}=[d_j \quad z_{xj} \quad z_{yj}]^T(j=1,2,..N_L)$
$d$：ロボット-ランドマーク間距離、$z_x$：$x$方向のランドマーク位置、
$z_y$：$y$方向のランドマーク位置、$N_L$：ランドマークの数
指令値
$\mathbf{u}=[u_v \quad u_\omega]^T$
$u_v$：速度指令値、$u_\omega$：角速度指令値
システムモデル
対向二輪モデル（ルンバみたいなモデル）です。

\mathbf{x_t} =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 0
\end{pmatrix}
\mathbf{x_{t-1}} +
\begin{pmatrix}
dt \cdot cos(\theta) & 0 \\
dt \cdot sin(\theta) & 0 \\
0 & dt \\
1 & 0  
\end{pmatrix}
\mathbf{u_t} + \mathbf{w}

$dt$：時間刻み

尤度
$ p(\mathbf{z}|\mathbf{x}) = \Sigma_{j=1}^{N_L}\frac{1}{\sqrt{2 \pi \sigma^2}} \cdot exp(-\frac{(d_j-\sqrt{(x-z_{xj})^2-(y-z_{yj})^2})^2}{2 \sigma^2})$
$ \sigma^2$：観測値の誤差分散

プログラム

"""

Ensemble Kalman Filter(EnKF) localization sample

Ref:
- [Ensemble Kalman filtering](https://rmets.onlinelibrary.wiley.com/doi/10.1256/qj.05.135)
"""

import numpy as np
import math
import matplotlib.pyplot as plt

#  Simulation parameter
Qsim = np.diag([0.2, np.deg2rad(1.0)])**2
Rsim = np.diag([1.0, np.deg2rad(30.0)])**2

DT = 0.1  # time tick [s]
SIM_TIME = 50.0  # simulation time [s]
MAX_RANGE = 20.0  # maximum observation range

# Ensemble Kalman filter parameter
NP = 20  # Number of Particle

show_animation = True


def calc_input():
    v = 1.0  # [m/s]
    yawrate = 0.1  # [rad/s]
    u = np.array([[v, yawrate]]).T
    return u


def observation(xTrue, xd, u, RFID):

    xTrue = motion_model(xTrue, u)

    z = np.zeros((0, 3))

    for i in range(len(RFID[:, 0])):

        dx = RFID[i, 0] - xTrue[0, 0]
        dy = RFID[i, 1] - xTrue[1, 0]
        d = math.sqrt(dx**2 + dy**2)
        if d <= MAX_RANGE:
            dn = d + np.random.randn() * Qsim[0, 0]  # add noise
            zi = np.array([dn, RFID[i, 0], RFID[i, 1]])
            z = np.vstack((z, zi))

    # add noise to input
    ud = np.array([[
        u[0, 0] + np.random.randn() * Rsim[0, 0],
        u[1, 0] + np.random.randn() * Rsim[1, 1]]]).T

    xd = motion_model(xd, ud)
    return xTrue, z, xd, ud


def motion_model(x, u):
    F = np.array([[1.0, 0, 0, 0],
                  [0, 1.0, 0, 0],
                  [0, 0, 1.0, 0],
                  [0, 0, 0, 0]])

    B = np.array([[DT * math.cos(x[2, 0]), 0],
                  [DT * math.sin(x[2, 0]), 0],
                  [0.0, DT],
                  [1.0, 0.0]])
    x = F.dot(x) + B.dot(u)

    return x


def calc_covariance(xEst, px):
    cov = np.zeros((3, 3))

    for i in range(px.shape[1]):
        dx = (px[:, i] - xEst)[0:3]
        cov += dx.dot(dx.T)

    return cov


def enkf_localization(px, xEst, PEst, z, u):
    """
    Localization with Ensemble Kalman filter
    """
    pz = np.zeros((z.shape[0], NP))  # Particle store of z
    for ip in range(NP):
        x = np.array([px[:, ip]]).T

        #  Predict with random input sampling
        ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0]
        ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1]
        ud = np.array([[ud1, ud2]]).T
        x = motion_model(x, ud)
        px[:, ip] = x[:, 0]

        for i in range(len(z[:, 0])):
            dx = x[0, 0] - z[i, 1]
            dy = x[1, 0] - z[i, 2]
            prez = math.sqrt(dx**2 + dy**2) + np.random.randn() * Qsim[0, 0]  # add noise
            pz[i, ip] = prez

    x_ave = np.mean(px, axis=1)
    x_dif = px - np.tile(x_ave, (NP, 1)).T

    z_ave = np.mean(pz, axis=1)
    z_dif = pz - np.tile(z_ave, (NP, 1)).T

    U = 1/(NP-1) * x_dif @ z_dif.T
    V = 1/(NP-1) * z_dif @ z_dif.T

    K = U @ np.linalg.inv(V)  # Kalman Gain

    px_hat = px + K @ (np.tile(z[:, 0], (NP, 1)).T - pz)

    xEst = np.average(px_hat, axis=1).reshape(4, 1)
    PEst = calc_covariance(xEst, px_hat)

    return xEst, PEst, px_hat


def plot_covariance_ellipse(xEst, PEst):  # pragma: no cover
    Pxy = PEst[0:2, 0:2]
    eigval, eigvec = np.linalg.eig(Pxy)

    if eigval[0] >= eigval[1]:
        bigind = 0
        smallind = 1
    else:
        bigind = 1
        smallind = 0

    t = np.arange(0, 2 * math.pi + 0.1, 0.1)

    # eigval[bigind] or eiqval[smallind] were occassionally negative numbers extremely
    # close to 0 (~10^-20), catch these cases and set the respective variable to 0
    try:
        a = math.sqrt(eigval[bigind])
    except ValueError:
        a = 0

    try:
        b = math.sqrt(eigval[smallind])
    except ValueError:
        b = 0

    x = [a * math.cos(it) for it in t]
    y = [b * math.sin(it) for it in t]
    angle = math.atan2(eigvec[bigind, 1], eigvec[bigind, 0])
    R = np.array([[math.cos(angle), math.sin(angle)],
                  [-math.sin(angle), math.cos(angle)]])
    fx = R.dot(np.array([[x, y]]))
    px = np.array(fx[0, :] + xEst[0, 0]).flatten()
    py = np.array(fx[1, :] + xEst[1, 0]).flatten()
    plt.plot(px, py, "--r")


def main():
    print(__file__ + " start!!")

    time = 0.0

    # RFID positions [x, y]
    RFID = np.array([[10.0, 0.0],
                     [10.0, 10.0],
                     [0.0, 15.0],
                     [-5.0, 20.0]])

    # State Vector [x y yaw v]'
    xEst = np.zeros((4, 1))
    xTrue = np.zeros((4, 1))
    PEst = np.eye(4)

    px = np.zeros((4, NP))  # Particle store of x

    xDR = np.zeros((4, 1))  # Dead reckoning

    # history
    hxEst = xEst
    hxTrue = xTrue
    hxDR = xTrue

    while SIM_TIME >= time:
        time += DT
        u = calc_input()

        xTrue, z, xDR, ud = observation(xTrue, xDR, u, RFID)

        xEst, PEst, px = enkf_localization(px, xEst, PEst, z, ud)

        # store data history
        hxEst = np.hstack((hxEst, xEst))
        hxDR = np.hstack((hxDR, xDR))
        hxTrue = np.hstack((hxTrue, xTrue))

        if show_animation:
            plt.cla()

            for i in range(len(z[:, 0])):
                plt.plot([xTrue[0, 0], z[i, 1]], [xTrue[1, 0], z[i, 2]], "-k")
            plt.plot(RFID[:, 0], RFID[:, 1], "*k")
            plt.plot(px[0, :], px[1, :], ".r")
            plt.plot(np.array(hxTrue[0, :]).flatten(),
                     np.array(hxTrue[1, :]).flatten(), "-b")
            plt.plot(np.array(hxDR[0, :]).flatten(),
                     np.array(hxDR[1, :]).flatten(), "-k")
            plt.plot(np.array(hxEst[0, :]).flatten(),
                     np.array(hxEst[1, :]).flatten(), "-r")
            #plot_covariance_ellipse(xEst, PEst)
            plt.axis("equal")
            plt.grid(True)
            plt.pause(0.001)


if __name__ == '__main__':
    main()

実行結果

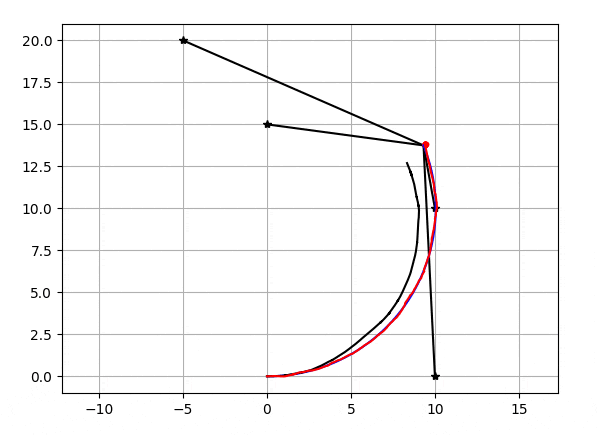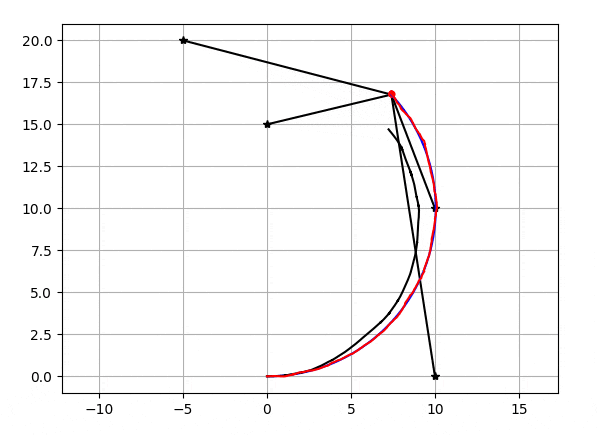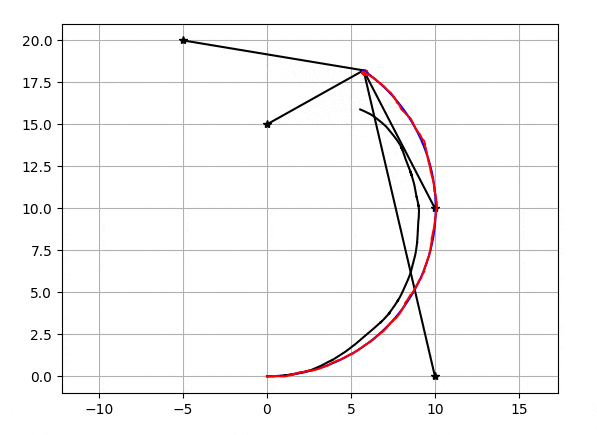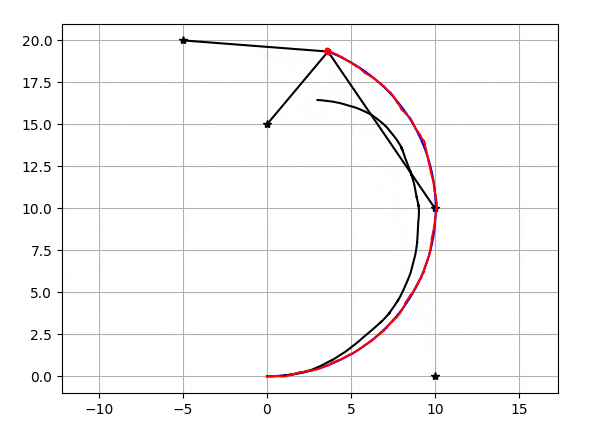
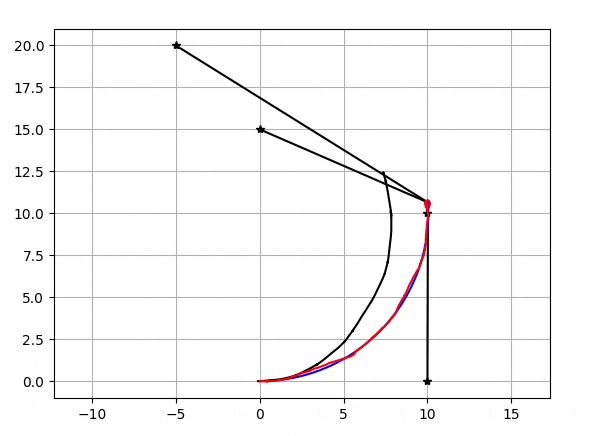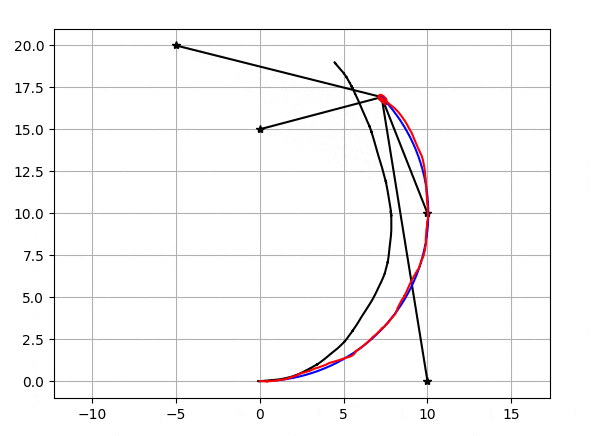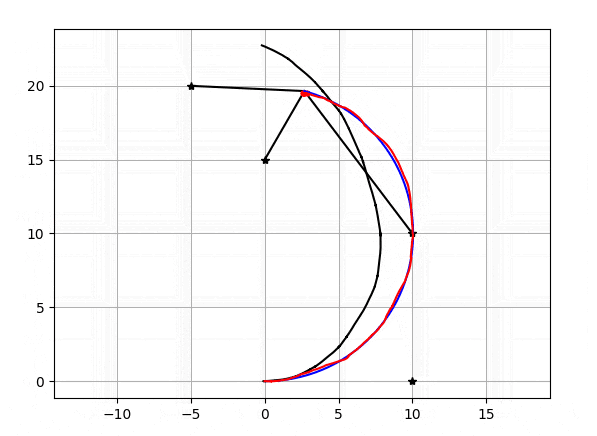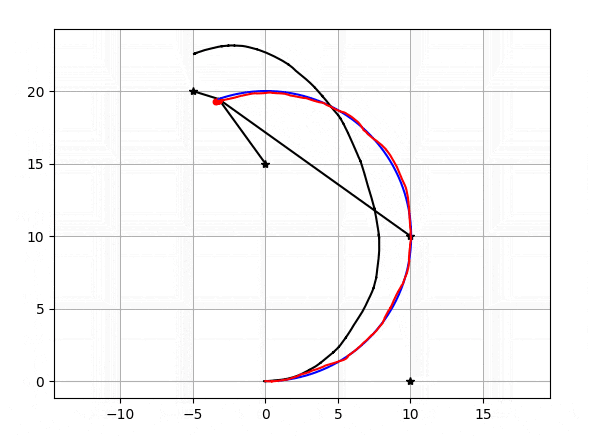
粒子数が20個の時のEnKFで自己位置推定の結果がこちらになります。

星がランドマーク、黒い直線がランドマーク-自己位置間距離、黒いグニャグニャしている線がデッドレコニング(ホイールオドメトリ/ジャイロ）の軌跡、青い線が真の軌跡、赤い線が推定された軌跡，赤い線の先端にあるのが粒子です。

~~(・・・粒子が見づらいので、パーティクルフィルターとの違いがわかり辛いですね・・・）~~

比較用に、粒子数が上のEnKFと同じ20個のParticle Filterで自己位置推定の結果が以下です。見てわかる通り、先端の粒子がワチャワチャしていて，うまく自己位置推定できていません。(このParticle FilterはPythonRoboticsのソースで粒子数を100個から20個に変えて回しています。)

EnKFはPFに比べうまく自己位置推定できていることが確認できます！

おわりに

今回はParticle Filterよりも少ない粒子数で自己位置推定できるEnsemble Kalman Filterを実装しました。
参考にしたPythonRoboticsは非常に読みやすく学習に最適なので、ロボットに興味ある方はぜひ！

コード置き場

片山,"非線形カルマンフィルタ",2011,p131-140 ↩

Ensemble Kalman Filter(EnKF)によるランドマークベースの自己位置推定 [PythonRobotics]