機械学習するロボットにギャンブルをやらせてみた

概要

動機

　最近、機械学習と深層学習という本を読み、「じゃあ、機械にギャンブルをやらせてみたらどうなるんだろう？」と発想したのがきっかけ。

手法

　今回は「どれだけお金をつぎ込んだらどれだけ儲かるまたは損をする」を学習させてみたいので、強化学習の一種でありサンプルプログラムが載っていた『Q学習』を用いた。

結論

　機械であっても期待値的には損をする行動もとるようになるらしい。

Q学習とは何なのか

　経路Qに対して報酬が与えられ、その報酬の多寡で学習を進めていく手法。

サンプルプログラム

　本に載っていたサンプルプログラムはCで書かれていたが、今更Cも何なのでRubyで書き換えた。本当はPythonなのかもしれないが、外部ライブラリを使っているわけでもなし、特別複雑な計算をしているわけでもなしで、Rubyでも大丈夫だと判断。
　ただし、関数selectaの中身はサンプルのデータ構造にものすごく依存した形で書かれていたので、そのデータ構造とこの後作りたいギャンブルが有限オートマトンで再現できることから、だいぶ書き換えた。この有限オートマトンをプログラムで再現する手法についてはこちらを参照してもらえればありがたい。

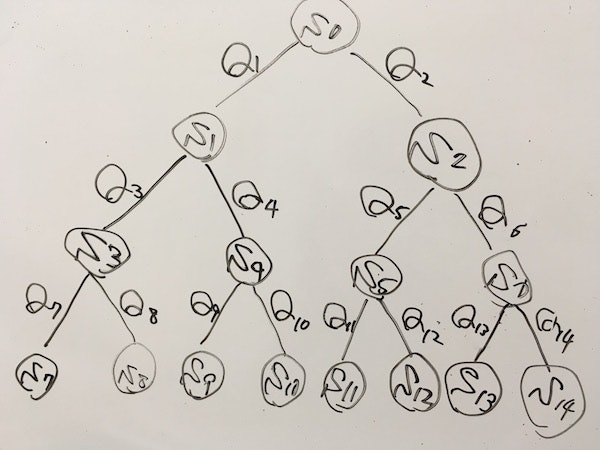
　以下のプログラムは、下図のS7~S14のゴールのうち、S14のゴールだけが正しいゴールだと学習するプログラムである。

qlearning.rb

def rand100 #0...100を返す乱数関数
  return Random.rand(0...100)
end

def rand1 #0~1の実数を返す乱数関数
  return Random.rand
end

def rand01 #0または1を返す乱数関数
  return [0,1].sample
end

# ε-greedy法による行動選択
def selecta(s, qvalue, state)

  if (rand1 < EPSILON) then
    if (rand01 == 0) then
      s = state[s][0]
    else
      s = state[s][1]
    end
  else
    if ((qvalue[state[s][0]]) > (qvalue[state[s][1]])) then
      s = state[s][0]
    else
      s = state[s][1]
    end
  end

  return s
end

def updateq(s, qvalue, state)
  qv = 0 #更新される値
  qmax = 0 #次のQ値の内で大きい方


  if (s > 6) then # 最下層にたどり着いたら
    if (s == 14) then # s==14がゴールなので、この時だけREWARDが得られる
      qv = qvalue[s] + ALPHA * (REWARD - qvalue[s])
    else
      qv = qvalue[s]
    end
  else
    if (qvalue[state[s][0]] > qvalue[state[s][1]]) then
      qmax = qvalue[state[s][0]]
    else
      qmax = qvalue[state[s][1]]
    end
    qv = qvalue[s] + ALPHA * (GAMMA * qmax - qvalue[s])
  end

  return qv
end

# Q値を出力する関数
def printQvalue (qvalue, j)
  printf("#{j},")
  for i in 1...NODENO do
    printf("#{qvalue[i]},")
  end
  printf("\n")
end

##### main #####

### 定数の設定 ###
GENMAX = 1000 #学習の繰り返し回数
NODENO = 15 #Q値のノード数
ALPHA = 0.1 #学習係数
GAMMA = 0.9 #割引率
EPSILON = 0.3 #行動選択のランダム性を決定
REWARD = 1000 #得られる報酬

qvalue = Array.new(NODENO) #Q値
state = [[1,2],[3,4],[5,6],[7,8],[9,10],[11,12],[13,14],
         [nil],[nil],[nil],[nil],[nil],[nil],[nil],[nil]] #状態遷移図

# Q値の初期化
for i in 0...NODENO do
  qvalue[i] = rand100
end

printf(",Q1,Q2,Q3,Q4,Q5,Q6,Q7,Q8,Q9,Q10,Q11,Q12,Q13,Q14,\n")

### 学習の本体 ###

for i in 0...GENMAX do
  s = 0 # 行動の初期状態

  until (state[s] == [nil]) do

    # 行動選択
    s = selecta(s, qvalue, state)

    # Q値の更新
    qvalue[s] = updateq(s, qvalue, state)
  end

  printQvalue(qvalue, i+1)

end

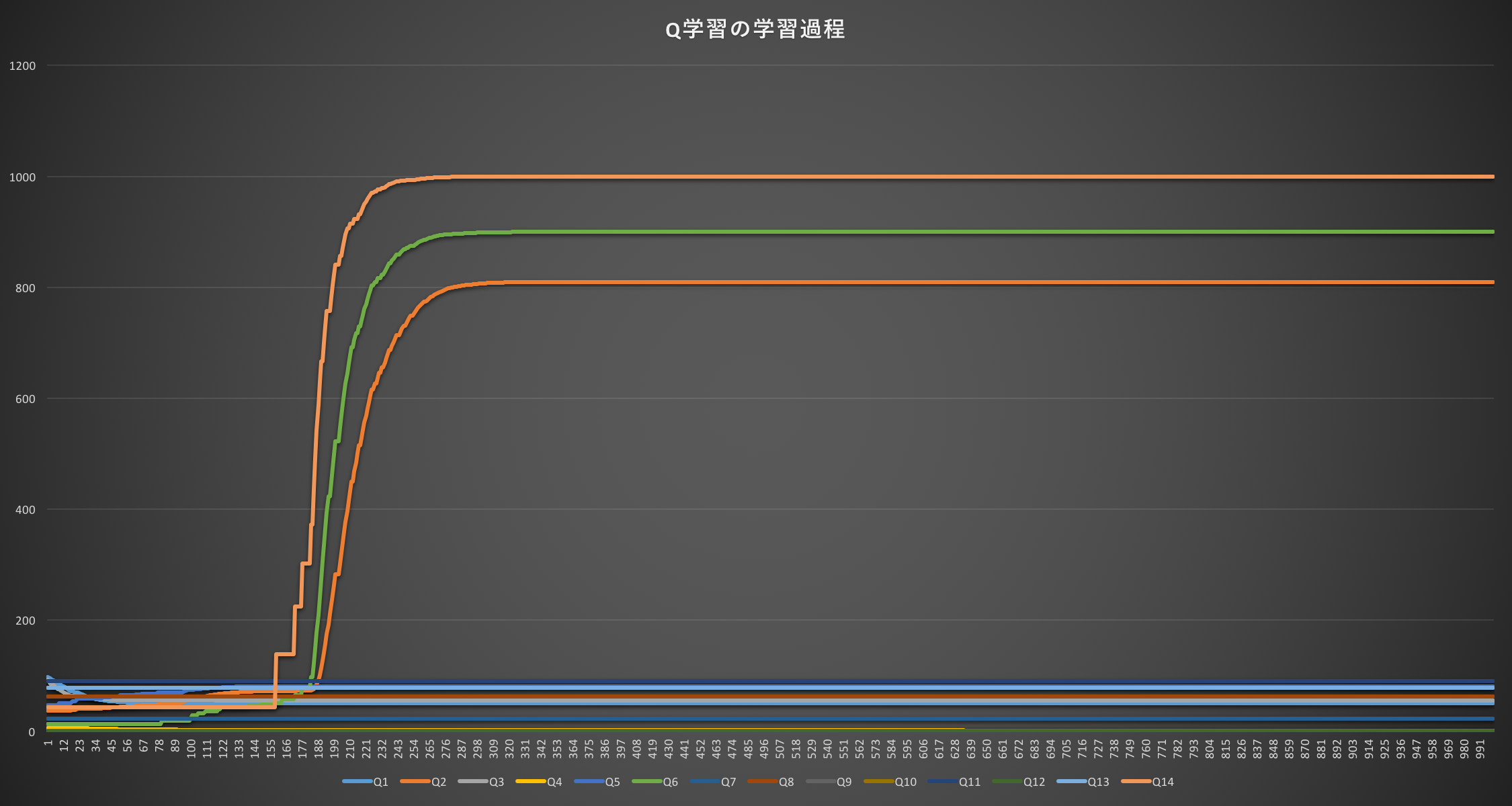
　これを実行したものをグラフにすると、以下の通り。

　しっかりと朱色のQ14のルート、緑色のQ6のルート、オレンジ色のQ2のルートが正しいルートだというように学習されている。

ギャンブルを学習させてみる

ギャンブルの状態遷移図

　今回のギャンブルでは、次のような状態遷移図を考えた。

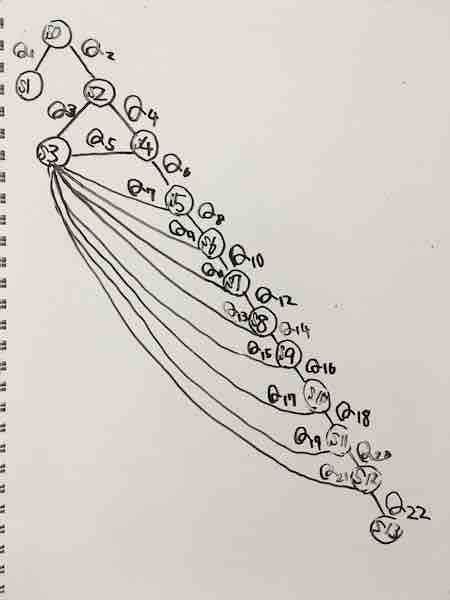
S0からスタートをし、S1は何もしないでギャンブルをやめるという選択、S2はギャンブルをやるという選択、それ以降はいつギャンブルをやめるかという選択。Q1とQ2だけはCOSTがかからないが、Q3以降は毎回COSTがかかる。S3にたどり着いた時、一定確率でREWARDが得られ、もしくはREWARDが得られなくてもお金だけは払って、ギャンブルをやめる。S13にたどり着いた時、つまりCOST*10の金額を払った時、お金だけ失って諦める選択になる。

プログラム

　サンプルプログラムでは、どのQを通ったかの添え字はたどり着いたSの添え字と同じだったためプログラムを簡略化したが、今回はSにたどり着いた時に通ったQは、state[s][1][0]もしくはstate[s][1][1]で表現している。
　また、Q値の初期化も報酬の桁が一桁増えたので、0~1000の値がランダムで入るように変更した。

def rand1000 #0...1000を返す乱数関数
  return Random.rand(0...1000)
end

def rand10 #0...10を返す乱数関数
  return Random.rand(0...10)
end

def rand1 #0~1の実数を返す乱数関数
  return Random.rand
end

def rand01 #0または1を返す乱数関数
  return [0,1].sample
end

# ε-greedy法による行動選択
def selecta(s, qvalue, state, way, cost_sum, cost)

  if (rand1 < EPSILON) then
    if (rand01 == 0) then
      way = state[s][1][0]
      s = state[s][0][0]
      cost_sum = cost_sum + cost[way]
    else
      way = state[s][1][1]
      s = state[s][0][1]
      cost_sum = cost_sum + cost[way]
    end
  else
    if ((qvalue[state[s][1][0]]) > (qvalue[state[s][1][1]])) then
      way = state[s][1][0]
      s = state[s][0][0]
      cost_sum = cost_sum + cost[way]
    else
      way = state[s][1][1]
      s = state[s][0][1]
      cost_sum = cost_sum + cost[way]
    end
  end

  return s, way

end

def updateq(s, qvalue, state, way, cost_sum)
  qv = 0 #更新される値
  qmax = 0 #次のQ値の内で大きい方

  if (s == 1) then
    # s == 1 に到達した時、何も得られないが、何も失わない。
    qv = qvalue[way] + ALPHA * (MONEY - qvalue[way])
  elsif (s == 3) then
    # S == 3 に到達した時、ランダムで報酬が手に入るか、お金だけ失って諦める。
    if (rand1 <= SEVEN) then
      qv = qvalue[way] + ALPHA * (REWARD + (MONEY - cost_sum) - qvalue[way])
      # qv = qvalue[way] + ALPHA * (REWARD[rand10] + (MONEY - cost_sum) - qvalue[way]) # REWARDをランダムにしたい場合、上行をコメントアウトしこの行頭のコメントアウトを外すこと
    else
      qv = qvalue[way] + ALPHA * ((MONEY - cost_sum) - qvalue[way])
    end
  elsif (s == 13) then
    # s == 12 に到達した時、お金だけ失って諦める
    qv = qvalue[way] + ALPHA * ((MONEY - cost_sum) - qvalue[way])
  else
    if (qvalue[state[s][1][0]] > qvalue[state[s][1][1]]) then
      qmax = qvalue[state[s][1][0]]
    else
      qmax = qvalue[state[s][1][1]]
    end
    qv = qvalue[way] + ALPHA * (GAMMA * qmax - qvalue[way])
  end

  return qv
end

# Q値を出力する関数
def printQvalue (qvalue, j)
  printf("#{j},")
  for i in 1...NODENO do
    printf("#{qvalue[i]},")
  end
  printf("\n")
end

##### main #####

### 定数の設定 ###
GENMAX = 10000 #学習の繰り返し回数
NODENO = 23 #Q値のノード数
ALPHA = 0.1 #学習係数
GAMMA = 0.9 #割引率
EPSILON = 0.3 #行動選択のランダム性を決定
REWARD = 20000 #得られる報酬
# REWARD = [3000, 3000, 3000, 3000, 3000, 5000, 5000, 5000, 10000, 20000]　# REWARDをランダムにしたい場合、上行をコメントアウトしこの行頭のコメントアウトを外すこと
COST = 3000 #一回行動するごとにかかるコスト
MONEY = 30000 #最初に持っているお金
SEVEN = 0.5 #当たりが出る確率

qvalue = Array.new(NODENO) #Q値
state = [[[1,2],[1,2]],[[nil],[nil]],[[3,4],[3,4]],[[nil],[nil]],[[3,5],[5,6]],
         [[3,6],[7,8]],[[3,7],[9,10]],[[3,8],[11,12]],[[3,9],[13,14]],[[3,10],[15,16]],
         [[3,11],[17,18]],[[3,12],[19,20]],[[3,13],[21,22]],[[nil],[nil]]] #状態遷移図

# costの初期化
cost = [0,0,0]
for i in 3...NODENO do
  cost.push(COST)
end

# Q値の初期化
for i in 0...NODENO do
  qvalue[i] = rand1000
end

printf(",Q1,Q2,Q3,Q4,Q5,Q6,Q7,Q8,Q9,Q10,Q11,Q12,Q13,Q14,Q15,Q16,Q17,Q18,Q19,Q20,Q21,Q22\n")

### 学習の本体 ###

for i in 0...GENMAX do
  s = 0 # 行動の初期状態
  cost_sum = 0
  way = 0

   until (state[s][0] == [nil])

     # 行動選択
     s, way = selecta(s, qvalue, state, way, cost_sum, cost)

     # Q値の更新
     qvalue[way] = updateq(s, qvalue, state, way, cost_sum)

  end

  printQvalue(qvalue, i+1)

end

結果

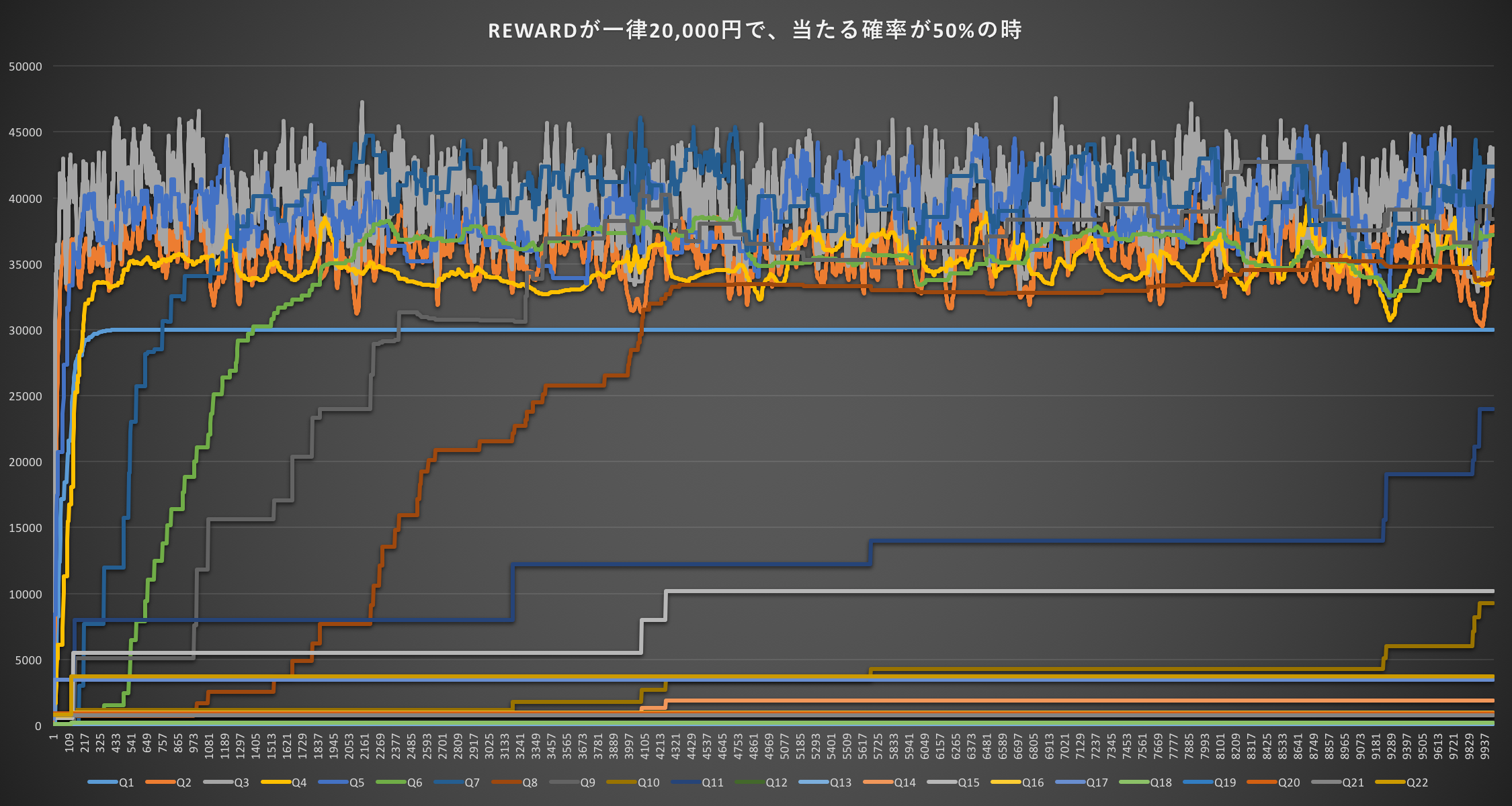
REWARDが一律20,000円で、当たる確率が50%の時(期待値10,000円)

　まず、Q1というギャンブルをしない選択肢よりもギャンブルをするという選択肢Q2以降の方が高い学習結果を示している。だいたいQ2〜Q9あたりがQ1よりも高くなっている。ここで注目するべきはQ9で、このルートにかかるcost_sumは12,000円だが、期待値である10,000円よりも高い。

　あとはステータスをいじって結果のみを出していく。

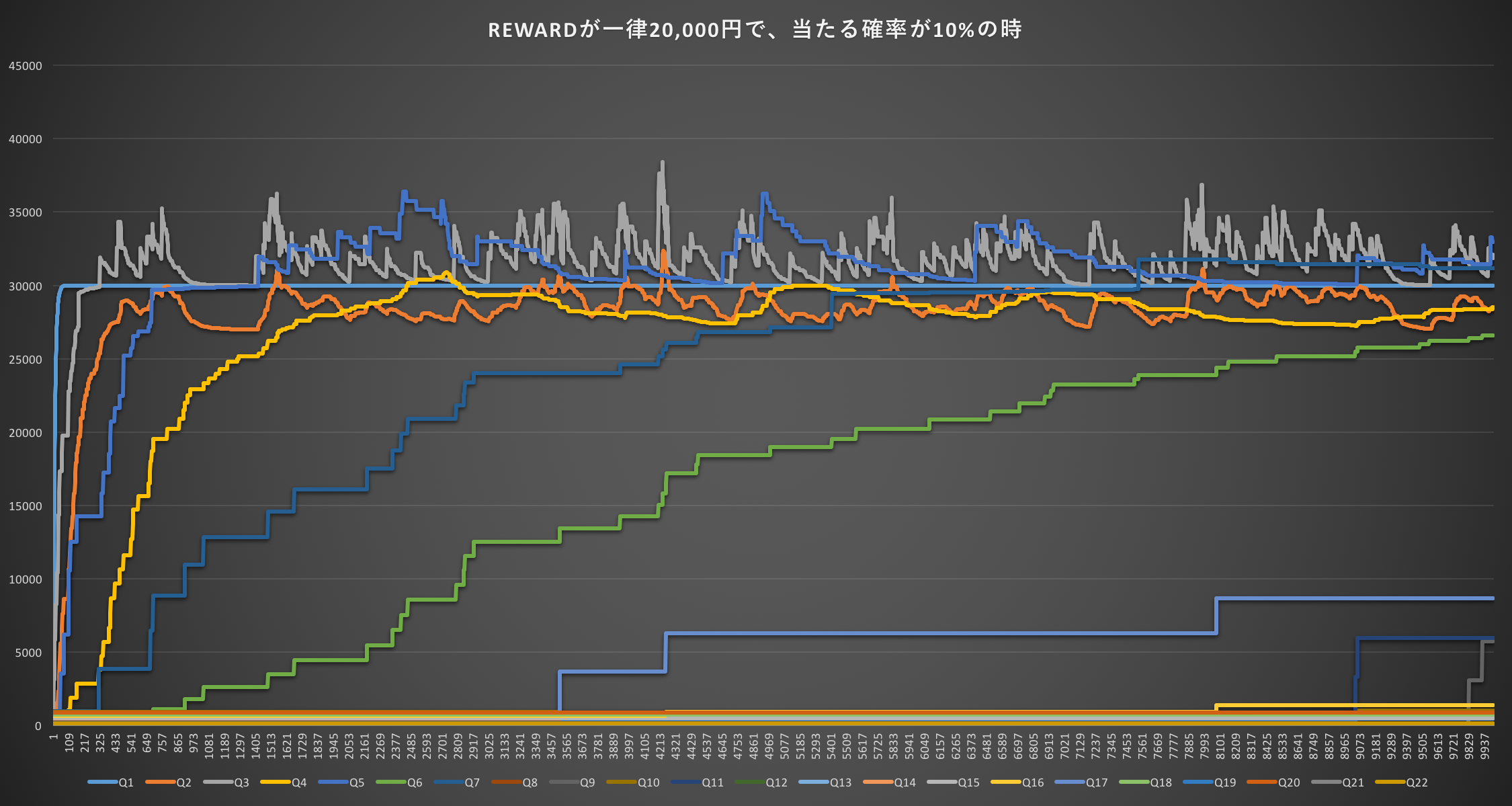
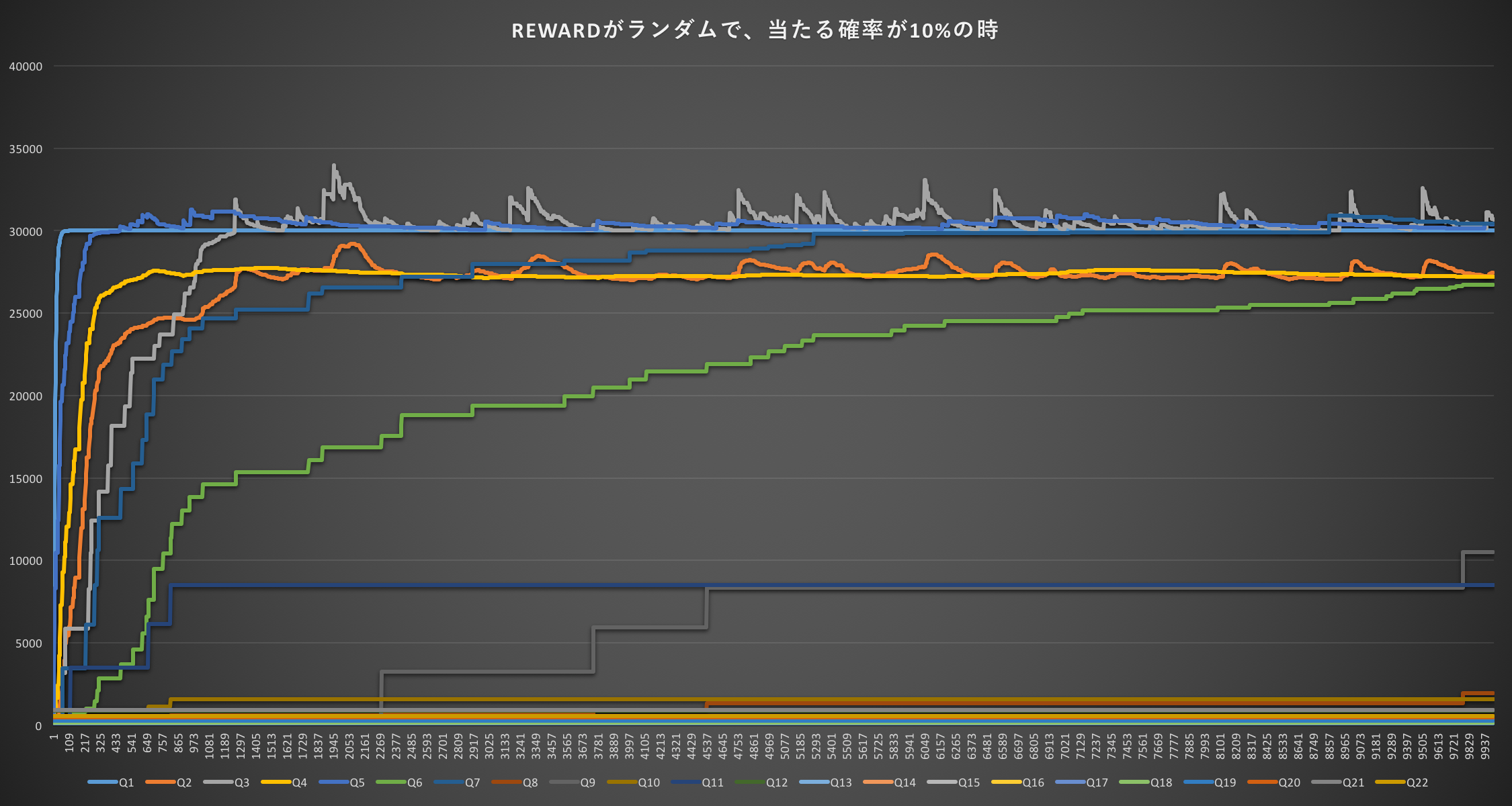
REWARDが一律20,000円で、当たる確率が10%の時（期待値2,000円）

　今回は期待値が2,000円なのだが、それよりも高いQ3(3,000円)やQ5(6,000円)、さらにだいぶ学習が進んだ後にはQ7(9,000円)がギャンブルをしないという選択肢であるQ1よりも高い値が出ている。

　では、REWARDが一律ではない場合はどうなのか？

REWARDがランダムで、当たる確率が10%の時（期待値600円）

　REWARD = [3000, 3000, 3000, 3000, 3000, 5000, 5000, 5000, 10000, 20000]という配列を作り、REWARD[rand10]を報酬とした場合。

　期待値が600円とかなり下がったが、それでもギャンブルをしない選択肢Q1よりも高い選択肢が出てきている。学習が進むとQ7(9,000円)の選択肢までQ1よりも高くなるのが興味深い。

まとめ

　まず、見た感じ機械もギャンブルをするという結果が出てきた。
　期待値が10,000円の時は、Q7(9,000円)までの選択肢であれば合理的であるので、最初の結果はギャンブルをすると言っても合理的であるかのように思える。が、この時も学習が進むとQ9(12,000円)のような期待値よりも高いコストを支払う行動が出てきた。
　この実験で注目すべきは、学習が進むほど不合理な選択肢を取っている、という点にある。人間で言うのならば、ギャンブルに浸るとギャンブル依存症になる、ということを表しているかのようだ。
　こうした不条理性が高いゲームに関しては、機械学習で解決策を見つけるのは非常に困難である、ということが言えるように思う。
　また個人的な教訓として、機械ですらギャンブル依存症になるのだから人間がギャンブルやっちゃダメー><!というようなことが学べた。心に留めおきたい。いや、本当に。