はじめに
業務でQ-Qプロットを書く必要があったため、さっそくQiitaをはじめ諸先輩方の知恵を拝借して手早く終わらせようと思いましたが、これが思いのほか手間取りました。「分位数」とか「累積分布関数」とかのキーワードを「ふ~ん」程度にしか理解しておらず、疑問点が多々生じたため、一度自分の中で整理することにしました。
Q-Qプロットとは
Qとは分位数(Quantile)を指しています。Q-Qプロットとは、観測したデータが従う確率分布モデルを調べたい時に、観測したデータの分位数$q_o$(Observed Quantile)と、仮定する確率分布モデルの分位数$q_p$(Predicted Quantile)を、$(x,y)$=$(q_o,q_p)$としてプロットしたものです。
たぶんここで、分位数って何だったっけ?となるので、身近に思って頂ける四分位数を使ってQ-Qプロットを作図していこうと思います。
四分位数によるQ-Qプロット
四分位数(Quartile)は、箱ひげ図と言われる統計の作図で登場する要約統計量のひとつです。ざっくりいうと、観測したデータを小さい順に並び替えたのち、四等分して、その境界の値を順に、「第1四分位」、「中央値(第2四分位)」、「第3四分位」と呼びます。
各四分位は、四等分しているため(ざっくり言えば)次が成り立ちます。
- 第1四分位は、下から25%の位置
- 第2四分位は、下から50%の位置
- 第3四分位は、下から75%の位置
実際に観測したデータに対して四分位を求めるには、必要に応じて補間をする必要があるかもしれません。(例えば、偶数個のデータのように50%の位置にデータが存在しない場合、その前後のデータから補間して求めるなど)また、四分位数の求め方は文科省の学習指導要領やExcelやRで定義が微妙に異なるようですが、データ数が十分に多ければ結果は同じになるようです。今回はnumpyのpercentileメソッドを利用しました。
\begin{align}
q_{oi} :& \text{観測値の第}i\text{四分位数}\\
p_{oi} :& \text{観測値の第}i\text{四分位数における累積確率}
\end{align}
一方で、仮定する確率分布モデルの四分位を求めるには、分位関数(Quantile Function, QF)を用います。これは要するに累積分布関数(Cumulative Distribution Function, CDF)の逆関数です。先ほど各四分位は下から○%の位置にあることが成り立つと言いましたが、これはつまり累積分布関数の縦軸が25%、50%、75%となるところの横軸を読めば、仮定する確率分布モデルに基づいて推定した四分位が求まります。今回はscipy.statsパッケージのppfメソッドを利用しました。
\begin{align}
q_{pi} &= CDF^{-1}(p_{pi})= QF(p_{pi})
\end{align}
\begin{align}
q_{pi} :& \text{予測値の第}i\text{四分位数}\\
p_{pi} :& \text{予測値の第}i\text{四分位数における累積確率}
\end{align}
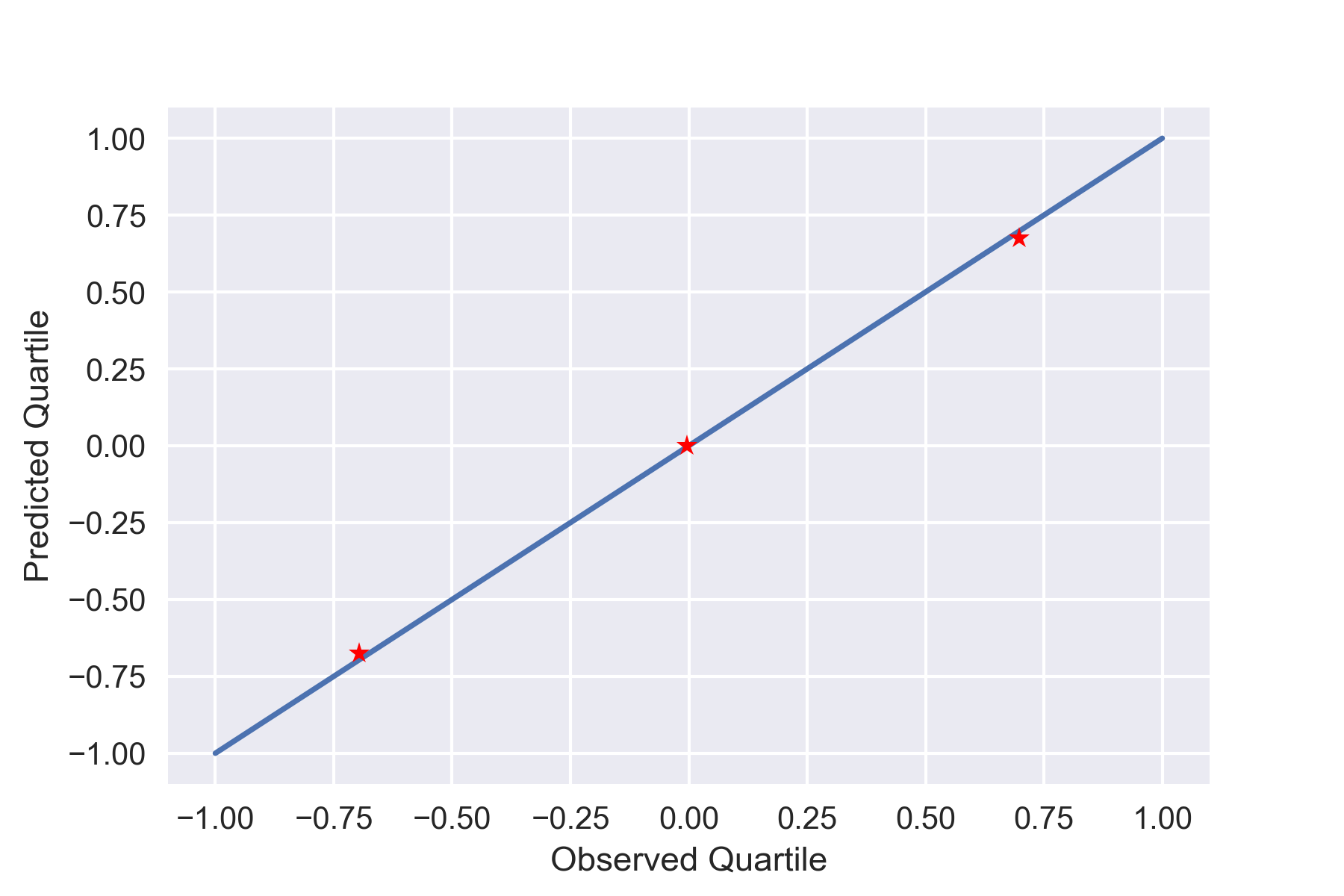
では早速、正規分布に従うデータを100点用意し、$p_{oi}=p_{pi}$(=25%、50%、75%)における観測したデータの四分位数$q_{oi}$と、正規分布の四分位数$q_{pi}$を、$(x,y)=(q_{oi},q_{pi})$としてプロットしてみます。
%matplotlib inline
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# calc
data = st.norm.rvs(size=100)
qo1 = np.percentile(data, 25) # observed first quartile
qo2 = np.percentile(data, 50) # observed second quartile
qo3 = np.percentile(data, 75) # observed third quartile
qp1 = st.norm.ppf(0.25) # predicted first quartile
qp2 = st.norm.ppf(0.50) # predicted second quartile
qp3 = st.norm.ppf(0.75) # predicted third quartile
# plot
plt.plot([qo1,qo2,qo3],[qp1,qp2,qp3],'r*')
plt.plot([-1,1],[-1,1])
plt.xlabel('Observed Quartile')
plt.ylabel('Predicted Quartile')
plt.savefig('qqplot_quartile.png',dpi=300)
一直線上に載っていますね!
つまり、観測したデータが正規分布である可能性が高いということです(当然ですが)。でも、Q-Qプロットというにはプロット点数が少し寂しいので、四分位数ではなくもっとたくさん分割した分位数でやれば、よく見るQ-Qプロットに近づくと思います。
また、図をよく見ると、第1四分位数と第3四分位数は直線からやや離れてプロットされているのがわかります。最初はデータ点数が少ないからだと思ってデータ点数を増やしてみましたが、むしろ直線からのずれが正確にあらわれることがわかりました。
m分位数によるQ-Qプロット
先ほどのやり方によるQ-Qプロットの欠点は、
- プロット点数が少ない
- 観測したデータの分位数を計算する際に補間が必要となる場合がある
でした。ここで、補間を必要としないためには、$m$分位数と観測したデータの位置がピッタリ合えばいいことになります。また、そうすることでデータ点数$n$だけプロット点数も取ることができます。$4$分位数ではプロット点を$3$個得たので、プロット点を$n$個にするために$n+1$分位数($m=n+1$)とします。
よって、観測したデータの$m$分位数を求めるには、データをソートするだけでよいです。こうすることで、$i$番目のデータは第$im$分位数ということになります。
\begin{align}
q_{pi} &= d_i
\end{align}
\begin{align}
d_i :& \text{ソートした後の第}i\text{番目の観測値}\\
q_{oi} :& \text{観測値の第}im\text{分位数}\\
p_{oi} :& \text{観測値の第}im\text{分位数における累積確率}
\end{align}
一方で、仮定する確率分布モデルの分位数は先ほどと同様に求めます。
\begin{align}
q_{pi} &= CDF^{-1}(p_{pi})= QF(p_{pi})
\end{align}
\begin{align}
q_{pi} :& \text{予測値の第}im\text{分位数}\\
p_{pi} :& \text{予測値の第}im\text{分位数における累積確率}
\end{align}
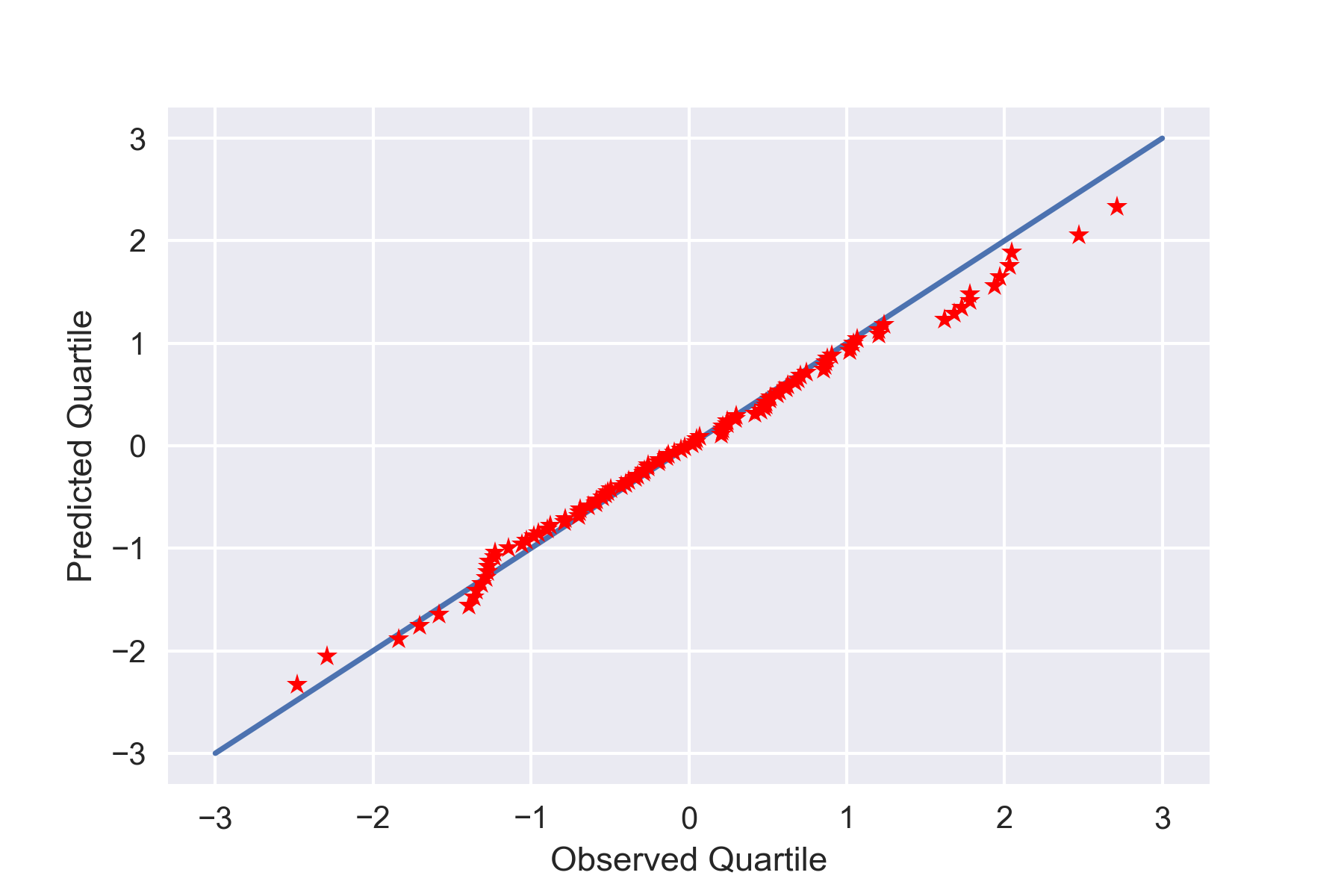
# calc
n=len(data)
m=n+1
ii=np.arange(n)+1 # i=1~n
qo=np.sort(data)
qp=st.norm.ppf( ii/m )
# plot
plt.plot([-3,3],[-3,3])
plt.plot(qo,qp,'r*')
plt.xlabel('Observed Quartile')
plt.ylabel('Predicted Quartile')
plt.savefig('qqplot.png',dpi=300)
Q-Qプロットらしくなってきました!
一方で、図をよく見ると直線に対して「プロットが寝ている」ように見えます。四分位数のQ-Qプロットの際に見つかった、直線からやや離れてプロットされている問題は健在のようです。
プロッティング・ポジション公式の適用
「プロットが寝ている」問題に対して、直線性を改善するためにプロッティング・ポジション公式を適用します。第$im$分位数の位置(○%、すなわち $p_{oi}$、$p_{pi}$)をこの公式で調整します。データ点数を$n$として、
\begin{equation}
p_i=\frac{i-\alpha}{n+1-2\alpha}
\end{equation}
\begin{align}
&\text{Weibull} & & \alpha=0 \\
&\text{Blom} & & \alpha=0.375 \\
&\text{Cunnane} & & \alpha=0.40 \\
&\text{Gringorten} & & \alpha=0.44 \\
&\text{Hazen} & & \alpha=0.50 \\
\end{align}
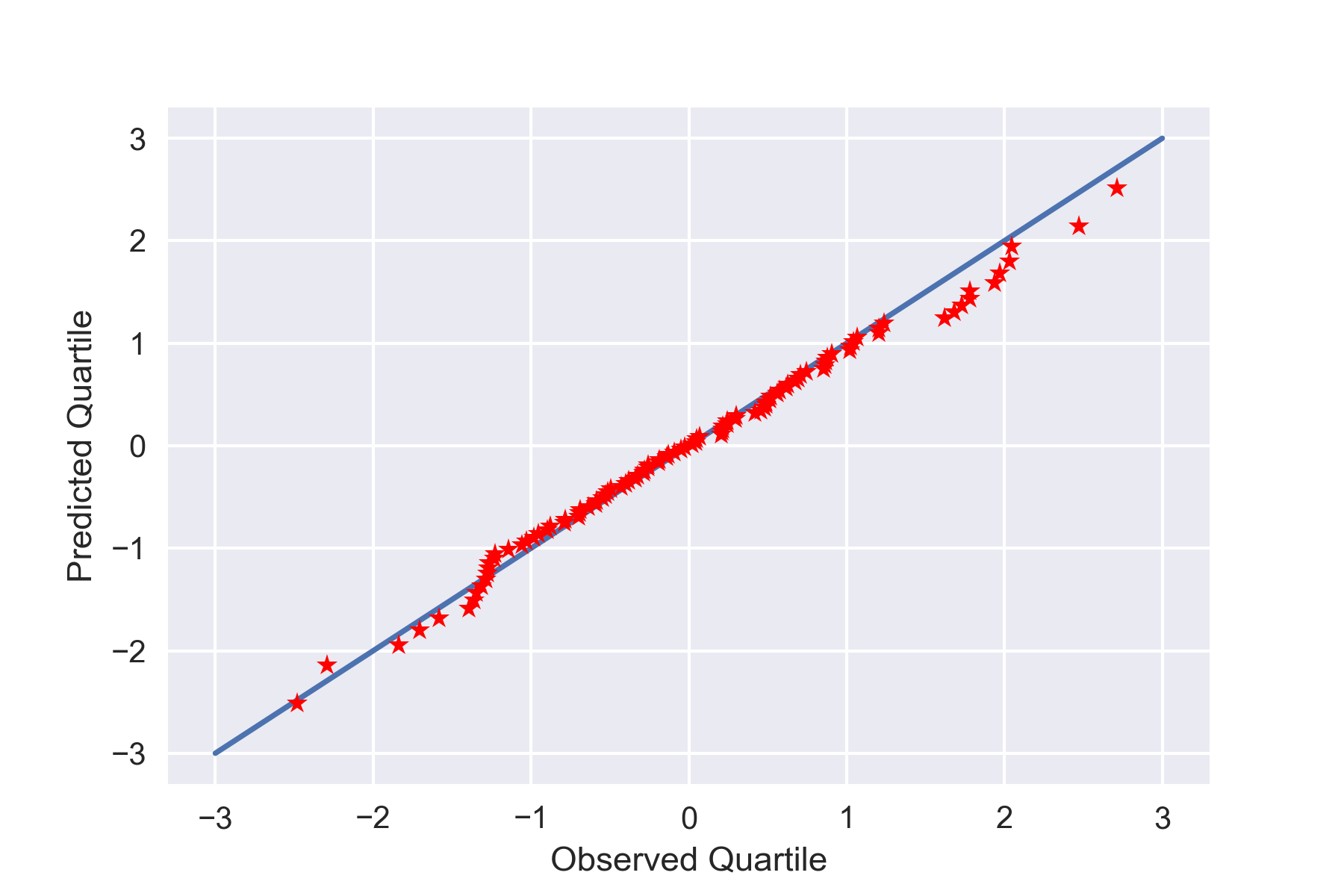
これによると、先ほどのQ-QプロットはWeibullの公式($\alpha=0$)を用いていたことがわかります。今度はこれをCunnaneの公式($\alpha=0.40$)にしてQ-Qプロットを描いてみます。
# calc
alpha=0.4
qo=np.sort(data)
qp=st.norm.ppf( (ii-alpha)/(n+1-2*alpha) )
# plot
plt.plot([-3,3],[-3,3])
plt.plot(qo,qp,'r*')
plt.xlabel('Observed Quartile')
plt.ylabel('Predicted Quartile')
plt.savefig('qqplot_cunnane.png',dpi=300)
よーく見ると、微妙に直線に近づいたような気がします(笑)。
Q-Qプロットを用いた実践例
Q-Qプロットの準備ができたので、観測したデータが従う確率分布モデルは何か調べてみましょう。
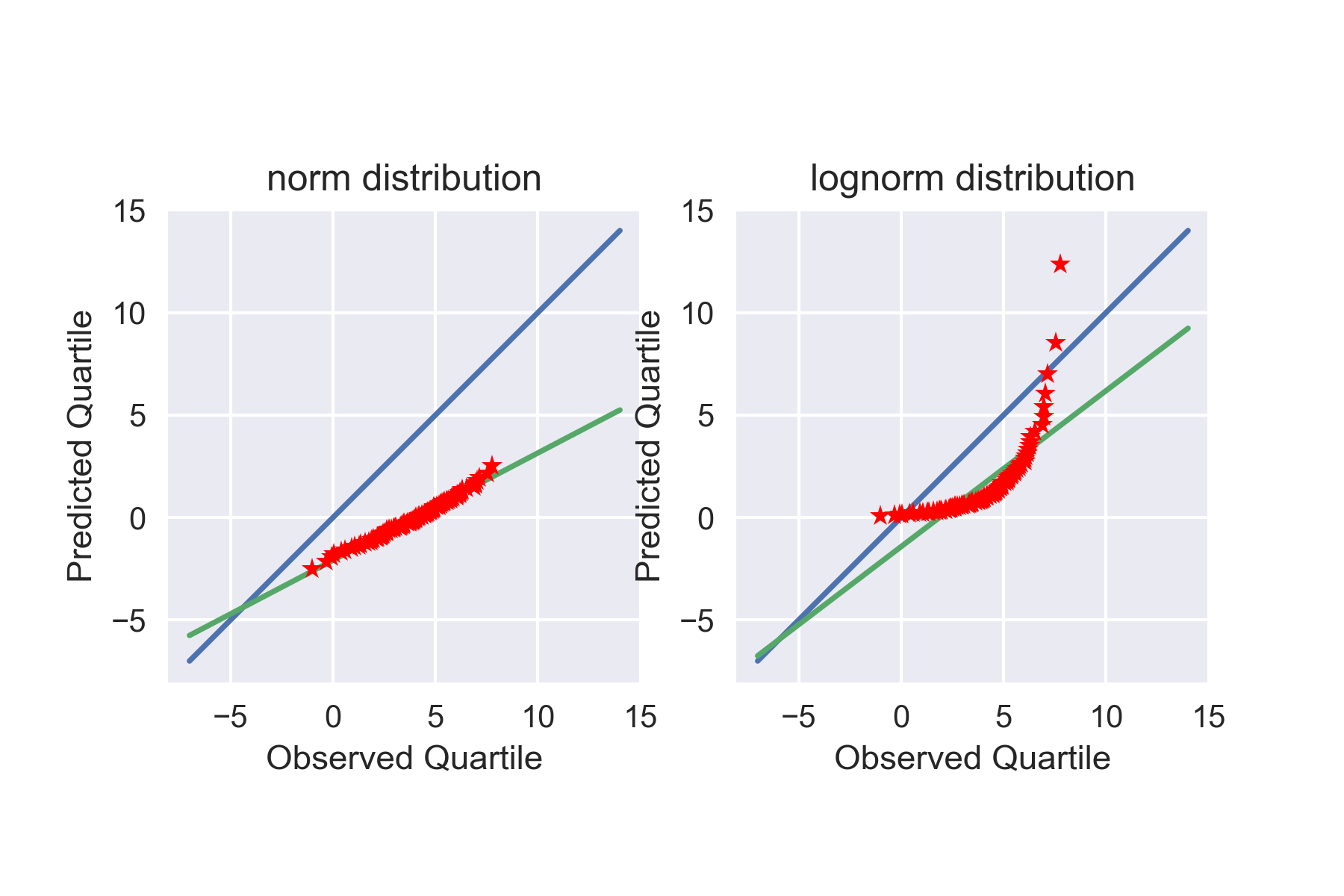
用意したデータは、平均4.0、標準偏差2.0の正規分布です。一方で、観測者はデータがどの確率分布モデルに従うかは知りません。よって、正規分布と対数正規分布の2つの確率分布モデルでそれぞれQ-Qプロットを描いてみることにします。
観測者は当然確率分布モデルのパラメータも分かりませんから、とりあえず平均0.0、標準偏差1.0としておきます。以前のコードではわざわざ書いていませんでしたが、書かずともデフォルトでloc=0.0, scale=1.0となっています。対数正規分布の方はs=1.0としておきます。
# create data
data = st.norm.rvs(size=100, loc=4, scale=2.0)
xrange = [-7,14]
# calc normal
alpha=0.4
qo=np.sort(data)
qp=st.norm.ppf( (ii-alpha)/(n+1-2*alpha), loc=0.0, scale=1.0 )
qx= xrange
qy= np.poly1d(np.polyfit(qo, qp, 1))(qx)
# plot
plt.subplot(1,2,1)
plt.plot(xrange, xrange)
plt.plot(qx, qy)
plt.plot(qo,qp,'r*')
plt.title('norm distribution')
plt.xlabel('Observed Quartile')
plt.ylabel('Predicted Quartile')
plt.gca().set_aspect('equal')
# calc log normal
alpha=0.4
qo=np.sort(data)
qp=st.lognorm.ppf( (ii-alpha)/(n+1-2*alpha) , s=1)
qx= xrange
qy= np.poly1d(np.polyfit(qo, qp, 1))(qx)
# plot
plt.subplot(1,2,2)
plt.plot(xrange, xrange)
plt.plot(qx, qy)
plt.plot(qo,qp,'r*')
plt.title('lognorm distribution')
plt.xlabel('Observed Quartile')
plt.ylabel('Predicted Quartile')
plt.gca().set_aspect('equal')
plt.savefig('qqplot_compare.png',dpi=300)
正規分布(左側)に対するQ-Qプロットの方が、直線になっています!
正規分布の場合は、比較する確率分布の母数(平均、標準偏差といった統計パラメータ)が分からなくとも、確率分布モデルが合っていればQ-Qプロットは直線となるため、直線か否かで観測したデータが正規分布なのか判断できます。また、描いたQ-Qプロットの切片や傾きから母数を推定することができるようです。
なお、他の確率分布モデルでは母数まで合わせないと直線になるとは限らないようですが、確率分布モデルごとに特殊なQ-Qプロットを用いることで母数に依存せず直線とすることができます。