はじめに
過去にカルマンフィルタについて独習した際のメモをQiitaでまとめることにしました。この記事では、はじめに時変カルマンフィルタについて取り扱ったのち、定常状態カルマンフィルタについて取り扱います。なお、記載の統一を図るため、数式や専門用語はMATLABのヘルプの表現に合わせています。
時変カルマンフィルタについて
カルマンフィルタは、限られたセンサから得られるノイズを含む情報から、その制御対象の「状態」を推定することができます。例えば、航空管制レーダの追跡システムにおいて、レーダに映るノイズを含んだ「航空機のレーダによる観測位置」が分かるとき、カルマンフィルタによって「航空機の尤もらしい位置」と「航空機の尤もらしい速度」を推定することができます。
まず、この航空管制レーダの追跡システムを離散時間の線形な状態空間モデルに落とし込みます。
\begin{align}
{x}[n+1] &= {Ax}[n]+{Gw}[n] \\
{y}[n] &= {Cx}[n]+{v}[n] \\
\end{align}
ここで、${x}$は状態ベクトル、${y}$は観測ベクトルを表します。
\begin{align}
{x}[n] &=
\begin{pmatrix}
航空機の真の位置 \\
航空機の真の速度
\end{pmatrix}\\
{y}[n] &= (航空機のレーダによる観測位置) \\
{w}[n] &= (プロセスノイズ) \\
{v}[n] &= (観測ノイズ) \\
\end{align}
航空機はほとんどの場合、等速直線運動と仮定してよいため、行列${A}$は等速直線運動を表す行列とします。プロセスノイズとは、等速直線運動から逸脱した動きをノイズとしてモデル化したものです。観測ノイズとは、レーダの測定誤差をノイズとしてモデル化したものです。プロセスノイズ${w}$、観測ノイズ${v}$の分散は以下のようにあらわします。$w$と$v$の相関はないものとします。
\begin{align}
{E}({w}{w}^T) &= Q \\
{E}({v}{v}^T) &= R \\
{E}({w}{v}^T) &= 0
\end{align}
ここで、カルマンフィルタによる推定値はハットを付けて表現することにします。状態ベクトルの推定値は$\hat x[n]$と表されます。このとき、推定値$\hat x$の真値$x$からの誤差の分散は以下のようにあらわします。
\begin{align}
E((x-\hat x)(x-\hat x)^T) &= P \\
\end{align}
カルマンフィルタは、共分散行列$P$を最小化するように設計されており、そのための仕組みとして予測ステップと修正ステップの2ステップによる処理を繰り返します。
予測ステップ
予測ステップでは、$n-1$番目から、$n$番目を予測します。
ここで、計算前の平滑値を$\hat Z_{n-1|n-1}$、計算後の予測値を$\hat Z_{n|n-1}$と表します。(Zは任意の値)
\begin{align}
\hat x_{n|n-1} &= A \hat x_{n-1|n-1} \tag{1} \\
P_{n|n-1} &= AP_{n-1|n-1}A^T +GQG^T \tag{2} \\
\end{align}
修正ステップ
予測ステップで求めた予測値に対し、観測値$y[n]$で修正します。
ここで、修正前の予測値を$\hat Z_{n|n-1}$、修正後の平滑値を$\hat Z_{n|n}$と表します。(Zは任意の値)
\begin{align}
M[n] &= P_{n|n-1}C^T(CP_{n|n-1}C^T+R)^{-1} \tag{3} \\
\hat x_{n|n} &= \hat x_{n|n-1} + M[n](y[n]-C \hat x_{n|n-1}) \tag{4} \\
P_{n|n} &= (I-M[n]C)P_{n|n-1} \tag{5} \\
\end{align}
ここで、$M[n]$はイノベーションゲインと呼びます。(4)を見ると、観測値と予測値の間でイノベーションゲインを割合とした内分式となっていることが分かります。つまり、イノベーションゲインが1に近づくほど、観測値を強く反映するようになります。
時変カルマンフィルタの状態空間モデルによる表現
時変カルマンフィルタは予測ステップと修正ステップによって計算できることを示しましたが、この章では制御工学で取り扱いやすい数式表現である、状態空間モデルで表してみます。ここで、MATLABでは以下の2種類の状態空間モデルを選択できます。
- 遅延推定器:入力を$y[n]$、出力を$\hat y_{n|n-1},\hat x_{n|n-1}$とする推定器
- 現在推定器:入力を$y[n]$、出力を$\hat y_{n|n},\hat x_{n|n}$とする推定器
まず、共通となる推定器の状態方程式を求めます。(1)に(4)を代入します。
\begin{align}
\hat x_{n+1|n} &= A \hat x_{n|n-1} + L[n](y[n]-C \hat x_{n|n-1}) \tag{6}\\
L[n] &= AM[n] \tag{7}
\end{align}
ここで、$L[n]$はゲイン行列と呼びます。
遅延推定器
予測ステップと修正ステップを統合し、予測値$\hat Z_{n|n-1}$を出力するようにした推定器(オブザーバ)です。出力のうち、$\hat x_{n|n-1}$は状態変数から直接求められます。また、制御対象の状態空間モデルから$\hat y_{n|n-1}=C \hat x_{n|n-1}$とすることで、出力方程式が以下のように求まります。
\begin{align}
\hat x_{n+1|n} &=
\begin{bmatrix}
A-L[n]C
\end{bmatrix}
\hat x_{n|n-1} &&+
L[n]
y[n] \tag{状態方程式}\\
\begin{bmatrix}
\hat y_{n|n-1} \\ \hat x_{n|n-1}
\end{bmatrix}
&=
\begin{bmatrix}
C \\ I
\end{bmatrix}
\hat x_{n|n-1} &&+
\begin{bmatrix}
0 \\ 0
\end{bmatrix}
y[n] \tag{出力方程式}\\
\end{align}
現在推定器
予測ステップと修正ステップを統合し、平滑値$\hat Z_{n|n}$を出力するようにした推定器(オブザーバ)です。出力のうち、$\hat x_{n|n}$は(4)から求められます。また、制御対象の状態空間モデルから$\hat y_{n|n}=C \hat x_{n|n}$とすることで、出力方程式が以下のように求まります。
\begin{align}
\hat x_{n+1|n} &=
\begin{bmatrix}
A-L[n]C
\end{bmatrix}
\hat x_{n|n-1} &&+
L[n]
y[n] \tag{状態方程式}\\
\begin{bmatrix}
\hat y_{n|n} \\ \hat x_{n|n}
\end{bmatrix}
&=
\begin{bmatrix}
(I-CM[n])C \\ I-M[n]C
\end{bmatrix}
\hat x_{n|n-1} &&+
\begin{bmatrix}
CM[n] \\ M[n]
\end{bmatrix}
y[n] \tag{出力方程式}\\
\end{align}
定常状態カルマンフィルタについて
先ほどまでは、共分散行列$P$を時変として取り扱ってきましたが、ここからは「定常状態」、すなわち共分散行列$P$を時不変として式展開を行います。(2)、(3)、(5)より、
\begin{align}
P_{n+1|n} &= A[P_{n|n-1} - P_{n|n-1}C^T(CP_{n|n-1}C^T+R)^{-1}CP_{n|n-1}]A^T +GQG^T \\
\end{align}
ここで、定常状態より$P_{n+1|n}=P_{n|n-1}=P$を用いて整理すると、
\begin{align}
P &= APA^T - APC^T(CPC^T+R)^{-1}(APC^T)^T +GQG^T \tag{DARE}\\
\end{align}
これは離散時間代数リカッチ方程式(Discrete-time Algebraic Riccati Equation:DARE)になります。この方程式を解くには、MATLABであれば、dare関数や、idare関数を用います。(DARE)の解を$P^*$とすると、(3)及び(7)より、
\begin{align}
M^* &= P^*C^T(CP^*C^T+R)^{-1} \\
L^* &= AM^* \\
\end{align}
$P$、$M$、$L$が時不変となったため、カルマンフィルタを線形時不変システム(LTIシステム)として取り扱うことができるようになります。
遅延推定器
\begin{align}
\hat x_{n+1|n} &=
\begin{bmatrix}
A-L^*C
\end{bmatrix}
\hat x_{n|n-1} &&+
L^*
y[n] \tag{状態方程式}\\
\begin{bmatrix}
\hat y_{n|n-1} \\ \hat x_{n|n-1}
\end{bmatrix}
&=
\begin{bmatrix}
C \\ I
\end{bmatrix}
\hat x_{n|n-1} &&+
\begin{bmatrix}
0 \\ 0
\end{bmatrix}
y[n] \tag{出力方程式}\\
\end{align}
現在推定器
\begin{align}
\hat x_{n+1|n} &=
\begin{bmatrix}
A-L^*C
\end{bmatrix}
\hat x_{n|n-1} &&+
L^*
y[n] \tag{状態方程式}\\
\begin{bmatrix}
\hat y_{n|n} \\ \hat x_{n|n}
\end{bmatrix}
&=
\begin{bmatrix}
(I-CM^*)C \\ I-M^*C
\end{bmatrix}
\hat x_{n|n-1} &&+
\begin{bmatrix}
CM^* \\ M^*
\end{bmatrix}
y[n] \tag{出力方程式}\\
\end{align}
MATLABよる実践例
MATLABで、時変カルマンフィルタと定常状態カルマンフィルタの双方を計算して比較してみました。時変カルマンフィルタは予測ステップと修正ステップを実装してforループで計算しています。一方で、定常状態カルマンフィルタは、kalman関数を用いてLTIシステムを生成して計算しています。なお、計算コードの作成にあたって、MATLABヘルプのカルマンフィルター設計を参考にしました。
function kalman_test
% PARAMTER
Ts=1;
% STEADY FILTER SYSTEM
f.A = [1.0, Ts; 0.0, 1.0];
f.B = zeros(2,0);
f.C = [1.0, 0.0];
f.D = zeros(1,0);
f.G = eye(2);
f.H = zeros(1,0);
f.Q = [3, 5; 5, 10];
f.R = [1];
sys_radar = ss(f.A, [f.B f.G], f.C, [f.D f.H],Ts);
[sys_kalman, L, P, M, Z] = kalman(sys_radar, f.Q, f.R, 'delayed');
% UNSTEADY FILTER SYSTEM
f.X = zeros(2,1); % initial state vector
f.P = f.G*f.Q*f.G'; % initial error covariance
% SIMULATION
t = (0:Ts:100)';
y = sin(t/5);
v = sqrt(f.R)*randn(length(t),1);
yv= y+v;
% STEADY FILTER SIMULATION
out = lsim(sys_kalman, yv);
yse = out(:,1);
% UNSTEADY FILTER SIMULATION
yue = zeros(length(t),1);
for i=1:length(t)
yue(i) = f.C*f.X;
f = correct_step(f, yv(i));
f = predict_step(f);
end
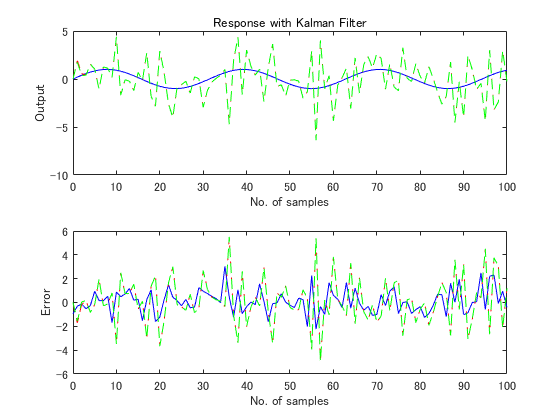
subplot(211), plot(t,y,'b',t,yue,'r--',t,yse,'g--'),
xlabel('No. of samples'), ylabel('Output')
title('Response with Kalman Filter')
subplot(212), plot(t,y-yv,'b',t,y-yue,'r--',t,y-yse,'g--'),
xlabel('No. of samples'), ylabel('Error')
Ls = L
Lu = f.A*f.M
Ps = P
Pu = f.P
Ms = M
Mu = f.M
end
function f = correct_step(f,y)
f.M = f.P*f.C'/(f.C*f.P*f.C'+f.R);
f.X = f.X + f.M*(y-f.C*f.X);
f.P = (eye(length(f.X))-f.M*f.C)*f.P;
end
function f = predict_step(f)
f.X = f.A*f.X;
f.P = f.A*f.P*f.A' + f.G*f.Q*f.G';
end
計算の実行結果は以下の通りです。定常状態カルマンフィルタで求めた緑の破線と、時変カルマンフィルタで求めた赤の破線がピッタリ重なっています。よって、どちらの計算方法でも同様の結果が得られることがわかります。
また、収束状態における時変カルマンフィルタと定常状態カルマンフィルタのゲイン行列$L$、共分散行列$P$及びイノベーションゲイン$M$も一致することがわかります。
Ls =
1.8415
0.9276
Lu =
1.8415
0.9276
Ps =
10.6222 10.7806
10.7806 14.8530
Pu =
10.6222 10.7806
10.7806 14.8530
Ms =
0.9140
0.9276
Mu =
0.9140
0.9276
まとめ
時変カルマンフィルタと定常状態カルマンフィルタの理論について、航空管制レーダの追跡システムで説明し、簡単なシミュレーションで実践しました。
ところで気になるのが、時変カルマンフィルタと定常状態カルマンフィルタの使いどころですが、実務においては、両方の手法を扱えた方が良いと感じています。双方のメリットを挙げてみます。
時変カルマンフィルタのメリット
- 定常状態カルマンフィルタでは扱えない、時変な状態空間モデルや共分散行列をもつ制御対象に使用できる。
- 初期値が定まらない場合でも、最適なイノベーションゲイン/ゲイン行列へ収束する。
定常状態カルマンフィルタのメリット
- 線形時不変システムとして取り扱うことができ、様々な評価ツールを利用できる。(安定性解析やボード線図等)
- 制御対象が厳密には時変システムであっても、検討初期における近似概算に利用できる。
- 上記の簡易シミュレーションのように時変カルマンフィルタの実装をテストできる。
より一般的なカルマンフィルタの定式化については、MATLABヘルプのKalmanFilterが非常に参考になります。