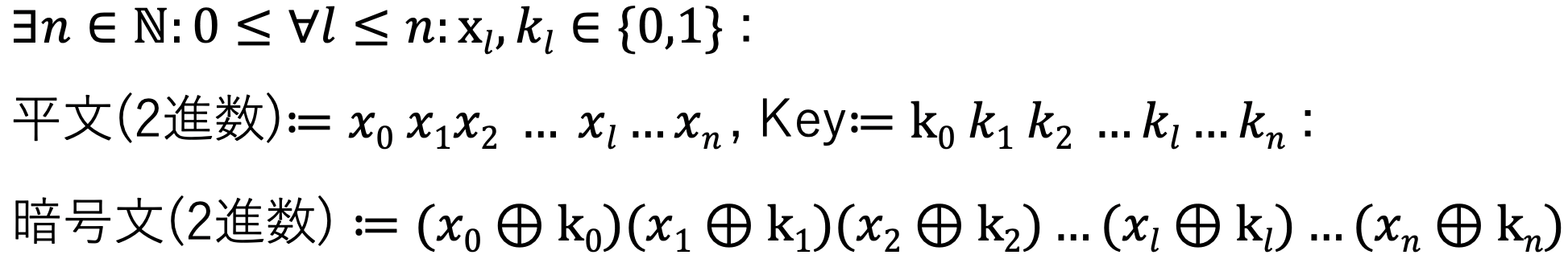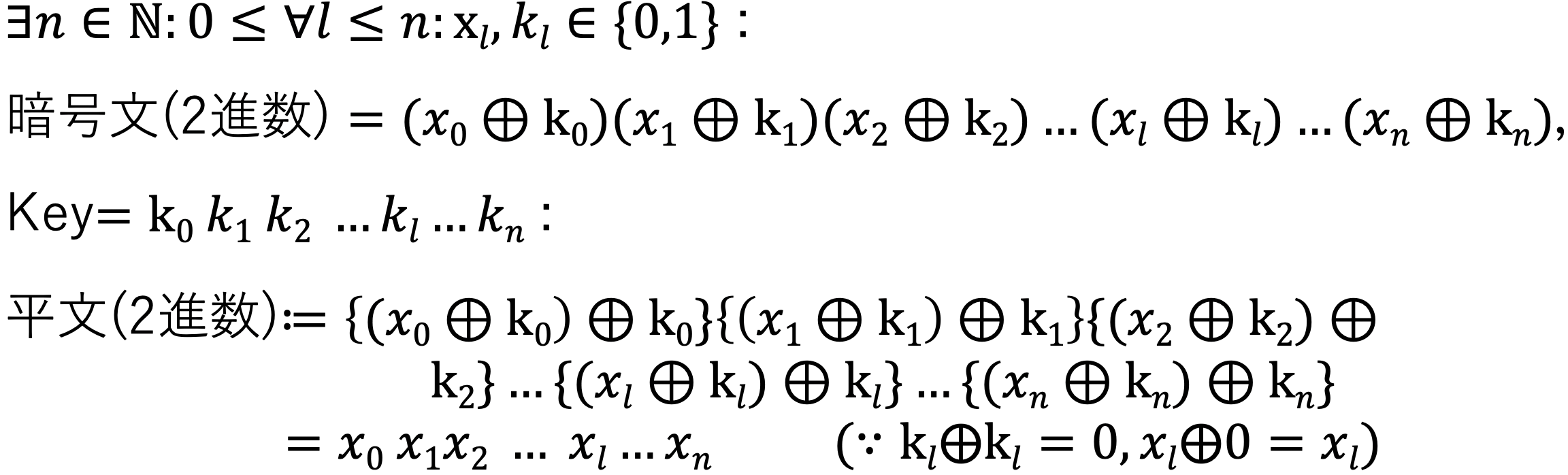バーナム暗号のアルゴリズム(Pythonで再現)

#前書き
0011110000111100011100110100011011100010010100011010111110000101010010011010011011001110111100111101011111011001110011001000001000101100100101001111101111001101011000100001110101011011111000001111101111010110000000000101110101011011111101000100111100011101000011100010010011101000011011010111011110011101001010000010110100011000011101110100011110001010110100000100101010011010111110110000010110110101000111011001101101001011111111110000001111100101011111100110100000000110100011110010001111111111101111100010101
(key:1001010110011111001111000111111011011110111010111100011001000010111110101000101001010000100001101110001110111100010001110011000100000011111110000100000001110111000010101001010011011100001011001110010110001011001101001011111010000010011000100011000101110111011101011101110010000000101111101111000100110011110001010001000010101010100001011010000000101101011101111101001000100001110010011110100101110110100101101110011101010111011000101011000100001011100101110110011100001000010000111001100001001101110111111100111)
#はじめに
ご安心ください，お使いのコンピュータは正常です...

それはさておき，みなさん，暗号はお好きですか？
暗号の歴史は古く，紀元前3000年前頃のものが存在を確認されています．

現存する最古の暗号は、紀元前 3000 年頃の石碑に描かれているヒエログリフ（古代エジプトで使われた 象形文字）であるとされています。
[引用元:https://www.digicert.co.jp/welcome/pdf/wp_encryption_history.pdf]

現代社会においても，暗号は特に情報通信の分野において非常に大きな役割を果たしています．詳しくはこちらをご覧ください．

本記事では共通鍵暗号の一つ，「バーナム暗号」について取り扱います．
#バーナム暗号の暗号化コード
暗号化の手順は以下の通りです．

1. 平文をnビット二進数に変換
2. KeyGenによって自動生成された,平文の二進数と同じサイズのnビット二進数を作成
3. 1,2で作成された二進数のそれぞれ対応する各ビットごとに排他的論理和をとってnビット二進数を作成(これが暗号文のnビット二進数)

すなわち...

それではこれをコーディングしていきます．

encryption．py

import random


def clear_to_ascii(ClearText):
    """
    1. 平文をnビット二進数に変換(今回はASCIIコードに変換する)
    """
    clear_ASCII_list = []
    for m in clearText:
        t = bin(ord(m))
        clear_ASCII_list.append(str(t)[2:])

    return "".join(clear_ASCII_list)


def KeyGen(n):
    """
    2. keyとなる平文の二進数と同じサイズのnビット二進数をランダム生成
    """
    key = ""
    for i in range(0, n):
        k = int(random.random() * 2)
        key = f"{key}{str(k)}"

    return key


def Enc(clear_ASCII, key, n):
    """
    3. 1,2で作成された二進数のそれぞれ対応する各ビットごとに排他的論理和をとってnビット二進数を作成
    """
    crypt_ASCII = ""
    for i in range(0, n):
        c = int(clear_ASCII[i]) ^ int(key[i])
        crypt_ASCII = f"{crypt_ASCII}{c}"

    return crypt_ASCII


if __name__ == "__main__":
    clearText = input('Clear text: ')
    n = len(clearText) * 7  # ASCIIコードはアルファベット一文字を7ビットの二進数で表すため
    key = KeyGen(n)
    print(f"　平:{clear_to_ascii(clearText)}\n")
    print(f"　鍵:{key}\n")
    print(f"暗号:{Enc(clear_to_ascii(clearText), key, n)}\n")

[注意: 今回のメインは暗号化であるため，平文からASCIIへの変換部分は簡略化しました(大文字，小文字アルファベットのみ対応．数字，記号を入れるとエラーが起きることがある).]

###実際に暗号化してみる
####入力

Clear text: hogehoge

####出力

　平:11010001101111110011111001011101000110111111001111100101
　鍵:10010011111001001001000110101101100011101000001000110001
暗号:01000010010110111010111111110000100101010111000111010100

上記の結果から，暗号の各ビットが，平文と鍵それぞれの各ビット同士の排他的論理和に対応していることがわかります．
実際に，この暗号のnビット二進数を無理やり文字列変換すると，"! u UcT "となり，"hogehoge"という文字列が暗号化されていることを確認できます．

#バーナム暗号の復号化コード
復号化は暗号化手順をほぼ逆から行えば良いだけです．

1. nビットの暗号と，暗号化の際に用いたnビットの鍵のそれぞれ対応する各ビットごとに排他的論理和をとってnビット二進数を作成(これが平文のnビット二進数)
2. 1で作成されたnビット二進数をアルファベットの文字列に変換する．

すなわち...

それではこれをコーディングしていきます．

decryption.py

def Dec(crypt_ASCII, key, n):
    """
    1. nビットの暗号と，nビットの鍵のそれぞれ対応する各ビットごとに排他的論理和をとってnビット二進数を作成
    """
    clear_ASCII = ""
    for i in range(0, n):
        c = int(crypt_ASCII[i]) ^ int(key[i])
        clear_ASCII = f"{clear_ASCII}{c}"

    return clear_ASCII


def ascii_to_clear(clear_ASCII, n):
    """
    2. nビット二進数をアルファベットの文字列に変換する．
    """
    v = [clear_ASCII[i: i+7] for i in range(0, n, 7)]

    clearText = ""
    for c in v:
        ch = chr(int(c, 2))
        clearText = f"{clearText}{ch}"

    return clearText


if __name__ == "__main__":
    crypt_ASCII = input("Cryptography(ASCII): ")
    key = input("key: ")
    n = len(key)
    print(f"平文: {ascii_to_clear(Dec(crypt_ASCII, key, n), n)}")

###実際に復号化してみる
先ほど暗号化によって出力した暗号文とkeyを用います．
####入力

Cryptography(ASCII): 01000010010110111010111111110000100101010111000111010100
key: 10010011111001001001000110101101100011101000001000110001

####出力

平文: hogehoge

先ほど暗号化の際に入力した平文"hogehoge"と一致していることが確認できます．
##ついでに...
実は前書きにおけるnビット二進数列もバーナム暗号になっているのです．
この暗号文とkeyをdecryption.pyに入力してみます．
####入力

Cryptography(ASCII): 0011110000111100011100110100011011100010010100011010111110000101010010011010011011001110111100111101011111011001110011001000001000101100100101001111101111001101011000100001110101011011111000001111101111010110000000000101110101011011111101000100111100011101000011100010010011101000011011010111011110011101001010000010110100011000011101110100011110001010110100000100101010011010111110110000010110110101000111011001101101001011111111110000001111100101011111100110100000000110100011110010001111111111101111100010101
key: 1001010110011111001111000111111011011110111010111100011001000010111110101000101001010000100001101110001110111100010001110011000100000011111110000100000001110111000010101001010011011100001011001110010110001011001101001011111010000010011000100011000101110111011101011101110010000000101111101111000100110011110001010001000010101010100001011010000000101101011101111101001000100001110010011110100101110110100101101110011101010111011000101011000100001011100101110110011100001000010000111001100001001101110111111100111

####出力

平文: ThisArticleIsTheEleventhDayArticleOfSophiaUniversityElelaboAdventCalendar

直訳すると

この記事は上智大学エレラボAdvent Calendar第11日目の記事です

となります．
上智大学エレラボAdvent Calendarには，サークルに属するメンバーの素晴らしい記事が多く掲載されているので，タイトルからいらっしゃった方も是非ご覧ください．

#まとめ
いかがでしたか？
排他的論理和の性質を利用した暗号...とても面白いと思います(個人の感想)．

バーナム暗号は1949年にShannonによって解読不可能であることが数学的に証明されている安全性の非常に高い暗号です．

しかし，平文のnビット二進数と同じサイズの鍵を用意しなければならないことから，効率が非常に悪い暗号と言えます．
このkeyのサイズをもう少し小さくできないか...ということで考案されたのがストリーム暗号と呼ばれる暗号です．この記事を読んで暗号に興味を持たれた方は是非，ストリーム暗号についても調べてみることをお勧めします．
##参考文献
IPUSIRON,暗号技術の全て,翔泳社,2017
↑暗号理論を一から学んでみたいという方にはお勧めの一冊です．