平行座標プロット

線の交差が少ない：正の相関
線の交差が多い：負の相関
イメージが湧かないのでとりあえず描いてみる。

matplotlibでは平行座標プロットの描画は組み合わせで作るしかないようです。
plotlyだと直接平行座標プロットを描画できるのでplotlyを使います。

#使うライブラリなど
import pandas as pd
import matplotlib.pyplot as plt
import plotly.express as px
from sklearn.datasets import load_iris
import seaborn as sns

量的変数の平行座標プロット

てきとうな例

身長と体重の量的変数2つ。
10人想定して、
BMIの式にほぼ当てはまる、身長高いほど体重が高いという正の相関を8人。
負の相関になる超モデル体系と超幸せ体系を2人作ってみる。

import pandas as pd

df = pd.DataFrame({
    "x" : [180,143,157,172,169,155,164,159,166,170],
    "y" : [43.5, 90.4, 53.2, 65.0, 62.8, 52.8 , 59.1, 55.6, 60.6, 63.5],
})

df

import matplotlib.pyplot as plt
# 散布図
plt.scatter(df["x"],df["y"])
plt.show()

量的変数の平行座標プロットの描画(10data)

import plotly.express as px
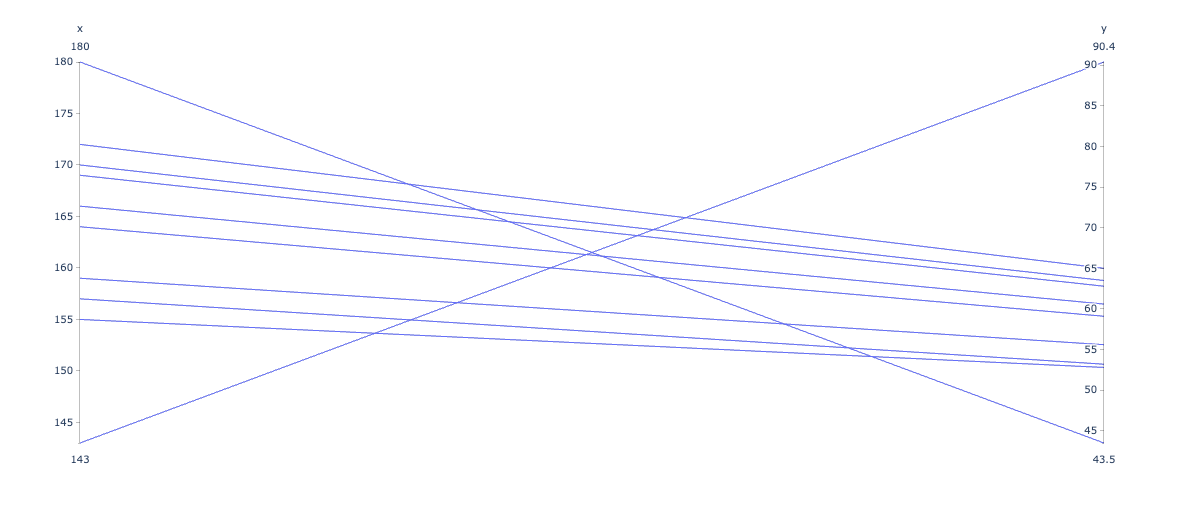
fig = px.parallel_coordinates(df, dimensions=["x","y"])
fig.show()

線の交差が少ない：正の相関。これは分かる。

線の交差が多い：負の相関。交差の数というより、中心で交わってたらって感じか。

というより、量的変数だと、この時点ですでに読み取りにくい。

量的変数の平行座標プロットの描画(150data)

irisをデータフレームにして、150dataに適用してみる。

# irisを格納
from sklearn.datasets import load_iris
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target

# 平行座標プロット
fig = px.parallel_coordinates(df, dimensions=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)',
       'petal width (cm)','target'])

fig.show()

やはり数が多くなれば、ここから相関について考えるのはなんかキツそうだ。目が痛い。
交差数で考えるのであれば、隣あうところとの関係しか分からない。

離れている変数同士の相関も分かるので、散布図行列やヒートマップを使った方が良さそうだ。

せめてtarget(irisの花のタイプ)毎に、どういう過程を経ているのかをみたい。
targetの0,1,2が実際は分類の変数なので、これで線を色分けするようにしてみる。

量的変数の平行座標プロットの描画を分類する

dimensionsからtargetを外す。色分けに使いたいのでcolorの指定先にtargetを指定。

fig = px.parallel_coordinates(df, dimensions=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)',
       'petal width (cm)'] ,color="target")

fig.show()

青が他の2つよりも明らかにpetallengthが短くて、petallengthを用いて青はデータセット上では完璧な分類ができることがわかる。

これも散布図行列を見れば良いが、これはこれで新鮮で良い。

分類を数値にしておけばiris.targetで0,1,2のint型でparallel_coordinatesの中に組み込める。
分類を直接 iris.target_namesで'setosa', 'versicolor', 'virginica'にするとエラーになってしまう。

parallel_coordinatesの中にはfloatとintが組み込める模様。
dtypeでobjectは弾かれる。

質的変数の平行座標プロット

てきとうな例

2値分類の質的変数2つを使う。
2×2クロス集計表で喫煙と肺癌を想定して、カイ二乗検定した時に有意（肺癌にタバコ関係ありそうだぞ）になるデータを作る。

# 質的変数（object型で格納）
smoke = ["なし"]*58 + ["あり"]*290
lung = ["Yes"]*11+["No"]*47+["Yes"]*163+["No"]*127
# dfにのっける
df = pd.DataFrame({
    "smoke" : smoke,
    "lung" : lung,
})
#  クロス集計表
pd.crosstab(df['smoke'], df['lung'])

質的変数2つの平行座標プロットの描画

parallel_coordinatesからカテゴリ変数になったということでparallel_categoriesに変えます。

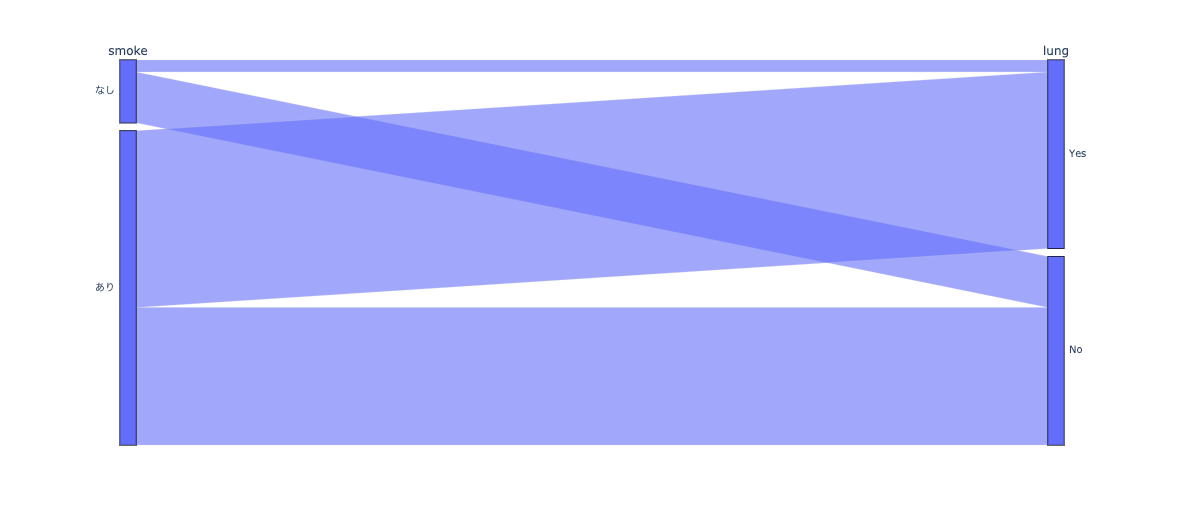
fig = px.parallel_categories(df, dimensions=["smoke","lung"])
fig.show()

質的変数の可視化という点では結構見やすい。
質的変数同士の場合散布図にしてしまうと点が重なってよく分からないが、重なりの密度を幅で教えてくれるのは助かる。

質的変数を複数にして平行座標プロットの描画

seabornのtipsというデータセットを使う。
このデータセットはfloat型2つ、int型1つ、category型4つで構成。
parallel_categoriesにデータフレームごと投げれば、
category型だけで平行座標プロットすると思ったら、

import seaborn as sns
df = sns.load_dataset("tips")
fig = px.parallel_categories(df)

fig.show()

category型だけでなく、int型も平行座標プロットされた。
intなら組み込めるということ？
それならfloatをint変換すれば？

# int型に変換する
df["total_bill"] = df["total_bill"].astype("int") # これだけプロットされない
df["tip"] = df["tip"].astype("int")
# 平行座標プロット
fig = px.parallel_categories(df)

fig.show()

変数が1つだけ落ちた。
落ちた変数はint型にしても3~50までまばらにある感じだったので、
categoriesの中に突っ込むint型におそらく上限があるのかも。

tipsというデータセットがtipをどれだけ貰えるかみたいな話だった気がするので、tipsで色分けしてみる。

# 平行座標プロット
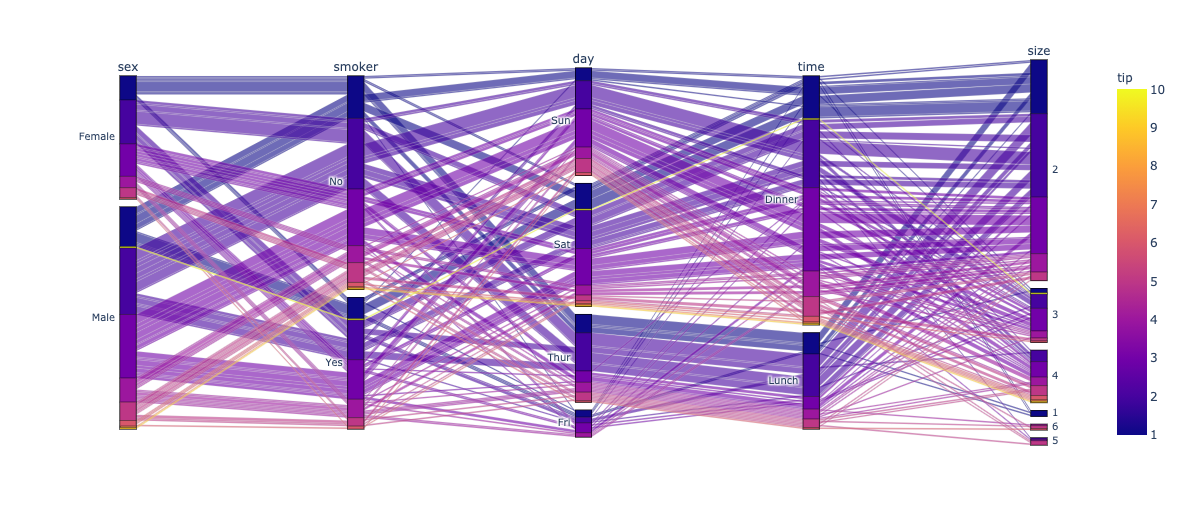
fig = px.parallel_categories(df, dimensions = ['sex', 'smoker', 'day', 'time', 'size'],color="tip")

fig.show()

tips自体が10分類なので、色変えてもみにくい。

高・中・低くらいで3分類すれば見やすくなるかも。

余裕があったらまた追記します。

まとめ

• 質的変数の可視化では便利かも。

• coordinatesはint,float。categoriesはobject,intを組み込めるようだ。

• 相関を感じるのは厳しくないか？

dtype混在型？

ここの最後に型が混在してそうな平行座標プロットがある。
df.dtypesで全てint型であるが質的変数も含んでいるかのように作られている。
作りたくなったら作ります。