単回帰モデル
最小二乗法(Ordinary Least Squares)を用いて単回帰モデルとそれに伴った色々なことを出していきます。
求めたいものを知るプログラムを末尾に載っけていてそれがメインで、序盤の理論的なところはかなり怪しいです。
今度テストがあるので、その対策でプログラムを作ったので、理論的なところ、用語の使い方は怪しさ満天です。
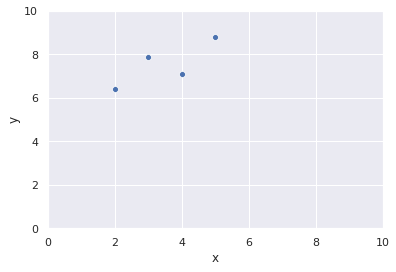
今回のデータ
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.DataFrame({
"x" : [2,3,4,5],
"y" : [6.4,7.9,7.1,8.8],
})
print(df)
sns.set()
sns.scatterplot(data=df, x="x", y="y")
plt.xlim(0,10)
plt.ylim(0,10)
plt.show()
説明変数をx,目的変数をyとして最小二乗法で単回帰モデルを作っていきます。
散布図に対して説明性が高いいい感じの直線を引きて〜!って感じです。
ただ、直線という制約があったら、全ての点を通るのは無理そうですよね。
ですので、いい感じということになります。
つまり、一生懸命いい感じの直線を引いたとしても、多少はその直線との誤差が出ることは避けられないということです。
でも、いい感じの直線を考えたいわけです。
できるだけ誤差が小さくなるように。
単回帰モデルの式
単回帰モデルは目的変数に対して説明変数は1つだけ。
説明変数が2つ以上になると重回帰モデルになります。
今回の単回帰モデルは
$$y_i = \beta_0 + \beta_1x_i + \epsilon_i\tag{1}$$
$\beta_0,\beta_1$:回帰係数
一次関数の式を思い出せば、$\beta_0$が切片、$\beta_1$が傾きに相当するところです。
切片と傾きが決まれば直線は引けたはずですから、
$\beta_0$、$\beta_1$を求めるというのが直線を引く上での大きな目的になるわけですね。
$\epsilon_i$:y軸方向の誤差(モデルで説明できなかった差)
直線という制約上全ての点を通る直線は引けないということから発生する、避けられない誤差の部分が$\epsilon_i$です。
$\epsilon_i$には仮定があって、
$\epsilon_i$〜$N(0,\sigma^2)$ としています。
平均:$0$ 分散:$\sigma^2$ の正規分布に従うということです。
この仮定のおかげで後々の式変形がうまく進みます。
(1)の式を$\epsilon_i$について変形すると
$$\epsilon_i =y_i - \beta_0 - \beta_1x_i $$
$\epsilon_i$がモデルで説明できなかった差であるということを考えると、
モデルを作る上では、モデルで説明できない差が小さければ小さいほど良いと考えるのが普通ですね。
ですので、各$\epsilon_i$をかき集めてきてきた和が最小になることを考えます。
ただ、そのまま$\epsilon_i$をかき集めると、符号の影響を受けてしまうので、誤差の最小の評価は二乗で考えることにします。
なんとなく最小二乗法っぽくなりました。
ここまでの話を整理して、目的は何か改めてみると
$$\sum\epsilon_i^2=\sum(y_i-\beta_0-\beta_1x_i)^2$$
これを最小にしてくれる $\beta_0,\beta_1$を推定して、いい感じの直線を引こうよ!ということです。
$\beta_0,\beta_1$は偏微分で解くのですが、省略します。
『最小二乗法 偏微分』とかググればいくらでも出てきます。
最小二乗推定量
$\beta_0,\beta_1$は推定値で出てくるので、
$\hat{\beta_0},\hat{\beta_1}$と表記します。
偏微分の結論だけを書くと、推定値は
$$\hat{\beta_1} = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}\tag{2}$$
$$\hat{\beta_0} = \bar{y}-\hat{\beta_1}\bar{x}$$
一応、文字の確認をしておくと、
$x_i$は$x$の$i$番目の数ということです。
$y_i$は$y$の$i$番目の数ということです。
$\bar{x}$はxとしている数の平均です。
$\bar{y}$はyとしている数の平均です。
ここまでpythonにしてみます。
import numpy as np
from scipy import stats
x = np.array([2,3,4,5])
y = np.array([6.4,7.9,7.1,8.8])
# 平均
x_mu = np.mean(x)
print("xの平均:{}".format(x_mu))
y_mu = np.mean(y)
print("yの平均:{}".format(y_mu))
# 回帰係数の推定に必要なもの
x_x_mu = x - x_mu # データと平均の差を格納
# print("x-x_mu:{}".format(x_x_mu)) numpyの配列で出てます。
y_y_mu = y - y_mu # データと平均の差を格納
# print("y-y_mu:{}".format(y_y_mu)) numpyの配列で出てます。
T_xy = np.sum(x_x_mu * y_y_mu) # 分子
T_xx = np.sum(x_x_mu**2) # 分母
T_yy = np.sum(y_y_mu**2) # 相関係数に使えるので出したおいた。
# 回帰係数の推定
beta1 = T_xy/T_xx
beta0 = y_mu - beta1*x_mu
print("beta1:{}".format(beta1))
print("beta0:{}".format(beta0))
print("回帰直線:y={}+{}x".format(beta0,beta1))
こんな感じで
$\hat{\beta_0}=5.31$
$\hat{\beta_1}=0.64$
と推定されました。
回帰係数が推定されるとどうなるかというと、
誤差は避けられないけどいい感じの直線というのが決まるわけです。
$$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i = 5.31+0.64x_i$$
$\hat{y_i}$は誤差が避けられない、いい感じ直線の式による予測値なので、誤差$\epsilon_i$は考慮されてません。
ただ、$\epsilon_i$は予測値$\hat{y_i}$と本当のデータ$y_i$の差として推定することはできそうです。
これを予測した結果、避けられなかった本当のデータとの誤差の推定値が残差$\hat{\epsilon_i}$です。
ここまでで分かっているのは、
予測値(いい感じの直線による値):
$$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i$$
残差:
$$\hat{\epsilon_i}= y_i - \hat{y_i}$$
ここまで揃ったら、次は推定したいい感じの直線の精度を考えていきます。
余談:最小二乗推定量と相関係数
$$\hat{\beta_1} = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}\tag{2}$$
この式がちょっと相関係数を求める式
$$r = \frac{Cov[X,Y]} {\sqrt{V[X]}\sqrt{V[Y]}}
=\frac{\frac{1}{n}\sum(x_i-\bar{x})(y_i-\bar{y})}
{\sqrt{\frac{1}{n}\sum(x_i-\bar{x})^2}\sqrt{\frac{1}{n}\sum(y_i-\bar{y})^2}}
=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2}\sqrt{\sum(y_i-\bar{y})^2}}\tag{3}
$$
に似てます。上が共分散っぽくなってて。
$r = U × \hat{\beta_1}$ を解くと
$U=\frac{\sqrt{\sum(x_i-\bar{x})^2}}{\sqrt{\sum(y_i-\bar{y})^2}}$
となるので、
$$r=\frac{\sqrt{\sum(x_i-\bar{x})^2}}{\sqrt{\sum(y_i-\bar{y})^2}}\hat{\beta_1}\tag{4}$$
という関係があることがわかります。
データが与えられているのであれば、相関係数はただデータを食わせれば出るので、どんな際に有用なのか、知っているとお得なことがあるのか、私にはわかりません。
# 相関係数
r_xy_1 = T_xy / np.sqrt(T_xx*T_yy) # (3)の式
print("相関係数:{}".format(r_xy_1))
r_xy_2 = np.sqrt(T_xx/T_yy)*beta1 # (4)の式
print("相関係数:{}".format(r_xy_2))
r_xy_3 = np.cov(x,y,ddof = 1)[0,1] / np.sqrt((np.var(x, ddof = 1)*np.var(y, ddof =1))) # 共分散と分散から
print("相関係数:{}".format(r_xy_3))
# 相関係数行列
print("相関係数行列")
print(np.corrcoef(x,y)) # データを食わせるだけ
当たり前ですが、全部同じ値が出ます。
モデルの精度を考える
準備1
単回帰モデル:
$$y_i = \beta_0 + \beta_1x_i + \epsilon_i$$
予測値(いい感じの直線):
$$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i$$
残差:
$$\hat{\epsilon_i}= y_i - \hat{y_i}$$
重相関係数:
$$Corr(y,\hat{y})$$
これらを使います。
# 予測値
y_hat = beta0 + beta1*x
print("予測値:{}".format(y_hat))
# 残差
residual = y - y_hat
residual
print("残差:{}".format(residual))
# 重相関係数
r_yy_hat = np.corrcoef(y,y_hat)[0,1]
print("重相関係数:{}".format(r_yy_hat))
準備2
回帰変動・残差変動・全変動を考えます。
変動なので、符号の影響を受けたくないので、全部二乗で考えます。
回帰変動(予測値):
$$\sum(\hat{y_i}-\bar{y})^2$$
自由度は説明変数の個数$k$
残差変動(残差):
$$\sum(\hat{\epsilon_i}-\bar{\epsilon})^2 = \sum\hat{\epsilon_i}^2$$
右の形を知っておけば良いと思いますが、
ここで$\epsilon_i$〜$N(0,\sigma^2)$の仮定が生きて、$\bar{\epsilon}=0$、になって左から右に進んでる感じですかね。
ここで残差変動だけ$\bar{\epsilon}$が記載されてないのは仮定のお陰ですかね。
自由度は $n-k-1$
$n$はデータの個数です。
(回帰変動の自由度)+(残差変動の自由度)=(全変動の自由度)
となるので、これで求めても良いです。
プログラムではこっちで求めてます。
全変動(応答):
$$\sum({y_i}-\bar{y})^2 $$
自由度はn-1
# 回帰変動
reg_v = np.sum((y_hat-y_mu)**2)
print("回帰変動:{}".format(reg_v))
# 残差変動
res_v = np.sum(residual**2)
print("残差変動:{}".format(res_v))
# 全変動
total_v = np.sum((y-y_mu)**2)
print("全変動:{}".format(total_v))
# 回帰変動の自由度
reg_free = x.reshape(-1,1).shape[1] # 説明変数xの配列を行列にして列の数をカウントしてます。
print("回帰変動の自由度:{}".format(reg_free))
# 全変動の自由度
total_free = len(x)-1
print("全変動の自由度:{}".format(total_free))
# 残差変動の自由度
res_free = total_free - reg_free
print("残差変動の自由度:{}".format(res_free))
実は自由度の個数だけでなく、
(回帰変動)+(残差変動)=(全変動) になっていることも分かります。
式を分解するとそうなります。
決定係数・自由度調整済み決定係数
準備ができたところで、モデルの評価をしていきます。
単回帰の場合は説明変数の選択がxのみ1通りなので、普通に決定係数で良いと思います。
自由度調整済み決定係数にすると、重回帰モデルで説明変数の個数が違うもの同士の精度を比較することができます。統計検定2級の問題でよく出てました。
決定係数
$$R^2=\frac{回帰変動}{全変動}=1-\frac{残差変動}{全変動}$$
$0≦R^2≦1$で評価されて、1であればあるほどモデルが良いということです。
説明変数を増やすほど$R^2$の値を大きくすることができてしまうという欠点があります。
それに対抗するのが自由度調整済み決定係数です。
重相関係数の2乗が決定係数に一致します。
$$R^2={Corr(y,\hat{y})}^2$$
# 決定係数
rsquared_1 = reg_v/total_v
print("決定係数:{}".format(rsquared_1))
rsquared_2 = 1 - (res_v/total_v)
print("決定係数:{}".format(rsquared_2))
rsquared_3 = r_yy_hat**2 # 重相関係数
print("決定係数:{}".format(rsquared_3))
考察
いつもこういう式を見ると、なんで1だといい評価ってなるの?って気になっちゃうので、考えてみることにしてます。
ここは勝手な考察なので、信憑性は怪しいですが、自分はこれで納得してます。
回帰変動:$\sum(\hat{y_i}-\bar{y})^2$
残差変動:$\sum\hat{\epsilon_i}^2$
全変動:$\sum({y_i}-\bar{y})^2$
この3つの式を見てみると、全変動にはハットの部分がないので、全変動は推定モデルに関係しない式です。
yの配列が分かれば推定も何もしなくても全変動は出るということです。
対して、回帰変動と残差変動はハットの部分が含まれるので、推定しなきゃ始まらない部分です。
$\frac{回帰変動}{全変動}$について
モデル関係なしに出てくる平均との差の2乗を合計した全変動
モデルを考慮して平均との差の2乗を合計した回帰変動が同じになる
$(回帰変動)=(全変動)$みたいな状況ができたらそれが理想な訳ですね。
この式の両辺を全変動で割れば、決定係数の評価の式になりますし、
左辺が1になるので理想状態で1なんだなぁ〜となんとなくわかるかなと。
$1-\frac{残差変動}{全変動}$について
残差変動はモデルが絡む部分ですが、$0$だと理想な訳です。
ということは
(モデルに関係ない部分)$-$(残差変動の理想値:$0$) $=$ (モデルに関係ない部分)
(全変動)$-$(残差変動) $=$ (全変動) が理想です。
これの両辺を全変動で割れば、やっぱり決定式の評価式の理想状態になって、それが1なんだなぁ〜となんとなく腑に落ちます。
本題に戻ります。
自由度調整済み決定係数
重回帰モデルで説明変数の個数が違うもの同士の精度を比較することができます。
$$\bar{R}^2=1-\frac{\frac{残差変動}{残差変動自由度}}{\frac{全変動}{全変動自由度}}$$
# 自由度調整済み決定係数
rsquared_adj = 1 - ((res_v/res_free) / (total_v/total_free))
print("自由度調整済み決定係数:{}".format(rsquared_adj))
回帰係数の区間推定
ここまでで推定してきたわけですが、
$$\hat{\beta_1} = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}$$
これは点推定です。
ここから区間推定をしていきます。
最小二乗推定量の分布
$$\hat{\beta_1} 〜 N(\beta_1,\frac{\sigma^2}{\sum(x_i-\bar{x})^2})$$
分母は$x_i$をその他の説明変数に回帰した時の残差平方和になる。
ただ、今回はその他の説明変数がないので、説明変数なしで回帰すると、横に一直線に伸びる直線でしか表現できない。そのため、残差が一番小さくなるように引くには平均値で横に伸びるしかない。
縦軸に$x$を取るとすると、回帰の結果は $x=\bar{x}$
よって他の説明変数に回帰した時の残差平方和は
$${\sum(x_i-\bar{x})^2}$$
なぜ他の説明変数に回帰した時の残差平方和を分母に使うかがしっくりこない。
ここに書いてあるよ〜とか詳しい方いたら教えてください。
母平均の推定を思い出してみる。
平均$\mu$、分散$\sigma^2$の小標本母集団からの抽出($t$分布を使うやつ)で母平均の信頼区間を推定したときのことを思い出すと
$\bar{X} 〜 N(\mu,\frac{\sigma^2}{n})$で標本平均$\bar{X}$、不偏分散を$\hat{\sigma}^2$とすると
不偏分散:
$$\hat{\sigma}^2=\frac{1}{n-1}\sum(x_i-\bar{x})^2$$
標準誤差
$$SE = \sqrt\frac{\hat{\sigma}^2}{n}$$
を用いて
$$ t = \frac{\bar{X}-\mu}{SE}$$
このtが自由度$n-1$の$t$分布に従うというやつです。
$$ -t_{0.025}≦\frac{\bar{X}-\mu}{SE}≦t_{0.025}$$
$$ \bar{X}-t_{0.025}SE
≦ \mu
≦\bar{X}+t_{0.025}SE$$
この辺りから論理的に理解していないのでこの場合と同じノリで回帰係数も推定します。
回帰係数の信頼区間を推定する
回帰係数の場合は
$$\hat{\beta_1} 〜 N(\beta_1,\frac{\sigma^2}{\sum(x_i-\bar{x})^2})$$
に従い、標本平均のところを$\hat{\beta_1}$、誤差の不偏分散を$\hat{\sigma}^2$とすると
誤差の不偏分散:
$$\hat{\sigma}^2
=\frac{1}{n-k-1}\sum\hat{\epsilon_i}^2
=\frac{1}{n-k-1}\sum({y_i-\hat{y_i}})^2$$
標準誤差:
$$SE(\hat{\beta_1}) = \sqrt\frac{\hat{\sigma}^2}{\sum(x_i-\bar{x})^2}$$
を用いて
$$ t = \frac{\hat{\beta_1}-\beta_1}{SE(\hat{\beta_1})}$$
このtが自由度$n-k-1$の$t$分布に従います。
$$ -t_{0.025}≦\frac{\hat{\beta_1}-\beta_1}{SE(\hat{\beta_1})}≦t_{0.025}$$
$$ \hat{\beta_1}-t_{0.025}SE(\hat{\beta_1})
≦ \beta_1
≦\hat{\beta_1}+t_{0.025}SE(\hat{\beta_1})
$$
これで回帰係数の推定、$\beta_1$の下限と上限が求まりました。
回帰係数の検定
帰無仮説:$H_0$:$\beta_1=0$
対立仮説:$H_1$:$\beta_1≠0$
xがyに関係ないんじゃないの?っていう検定です。
$t$の式で$\beta_1=0$を考えればいいので、
帰無仮説を想定した上での$t$値は 回帰係数の推定値 $÷$ 標準誤差 で出ます。
これも出力結果の読み取りで統計検定2級によく出てました。
# 誤差分散(不偏分散で置き換え)
sigma_var = res_v/res_free
print("誤差分散:{}".format(sigma_var))
# 回帰係数の標準誤差
beta1_se = np.sqrt(sigma_var/sum((x - x_mu)**2))
print("回帰係数の標準誤差:{}".format(beta1_se))
# 自由度に基づいたt分布のパーセント点
t_975 = stats.t.ppf(0.975,len(x)-x.reshape(-1,1).shape[1]-1)
t_975
# 回帰係数の上限・下限
beta1_up = beta1 + t_975*beta1_se
print("回帰係数の上限値:{}".format(beta1_up))
beta1_low = beta1 - t_975*beta1_se
print("回帰係数の下限値:{}".format(beta1_low))
# 帰無仮説:beta1 = 0 とした場合のt値
t_value1 = beta1/beta1_se
print("t_value:{}".format(t_value1))
プログラムを最後にまとめておきます。
プログラム
import numpy as np
from scipy import stats
# ここだけ変えてね
x = np.array([2,3,4,5])
y = np.array([6.4,7.9,7.1,8.8])
# 平均
x_mu = np.mean(x)
print("xの平均:{}".format(x_mu))
y_mu = np.mean(y)
print("yの平均:{}".format(y_mu))
# 回帰係数の推定に必要なもの
x_x_mu = x - x_mu
# print("x-x_mu:{}".format(x_x_mu))
y_y_mu = y - y_mu
# print("y-y_mu:{}".format(y_y_mu))
T_xy = np.sum(x_x_mu * y_y_mu)
T_xx = np.sum(x_x_mu**2)
T_yy = np.sum(y_y_mu**2)
# 回帰係数の推定
beta1 = T_xy/T_xx
beta0 = y_mu - beta1*x_mu
print("beta1:{}".format(beta1))
print("beta0:{}".format(beta0))
print("回帰直線:y={}+{}x".format(beta0,beta1))
# 相関係数
r_xy_1 = T_xy / np.sqrt(T_xx*T_yy)
print("相関係数:{}".format(r_xy_1))
r_xy_2 = np.sqrt(T_xx/T_yy)*beta1
print("相関係数:{}".format(r_xy_2))
r_xy_3 = np.cov(x,y,ddof = 1)[0,1] / np.sqrt((np.var(x, ddof = 1)*np.var(y, ddof =1)))
print("相関係数:{}".format(r_xy_3))
# 相関係数行列
print("相関係数行列")
print(np.corrcoef(x,y))
# 予測値
y_hat = beta0 + beta1*x
print("予測値:{}".format(y_hat))
# 残差
residual = y - y_hat
residual
print("残差:{}".format(residual))
# 重相関係数
r_yy_hat = np.corrcoef(y,y_hat)[0,1]
print("重相関係数:{}".format(r_yy_hat))
# 回帰変動
reg_v = np.sum((y_hat-y_mu)**2)
print("回帰変動:{}".format(reg_v))
# 残差変動
res_v = np.sum(residual**2)
print("残差変動:{}".format(res_v))
# 全変動
total_v = np.sum((y-y_mu)**2)
print("全変動:{}".format(total_v))
# 回帰変動の自由度
reg_free = x.reshape(-1,1).shape[1]
print("回帰変動の自由度:{}".format(reg_free))
# 全変動の自由度
total_free = len(x)-1
print("全変動の自由度:{}".format(total_free))
# 残差変動の自由度
res_free = total_free - reg_free
print("残差変動の自由度:{}".format(res_free))
# 決定係数
rsquared_1 = reg_v/total_v
print("決定係数:{}".format(rsquared_1))
rsquared_2 = 1 - (res_v/total_v)
print("決定係数:{}".format(rsquared_2))
rsquared_3 = r_yy_hat**2
print("決定係数:{}".format(rsquared_3))
# 自由度調整済み決定係数
rsquared_adj = 1 - ((res_v/res_free) / (total_v/total_free))
print("自由度調整済み決定係数:{}".format(rsquared_adj))
# 誤差分散(不偏分散で置き換え)
sigma_var = res_v/res_free
print("誤差分散:{}".format(sigma_var))
# 回帰係数の標準誤差
beta1_se = np.sqrt(sigma_var/sum((x - x_mu)**2))
print("回帰係数の標準誤差:{}".format(beta1_se))
# 自由度に基づいたt分布のパーセント点
t_975 = stats.t.ppf(0.975,len(x)-x.reshape(-1,1).shape[1]-1)
t_975
# 回帰係数の上限・下限
beta1_up = beta1 + t_975*beta1_se
print("回帰係数の上限値:{}".format(beta1_up))
beta1_low = beta1 - t_975*beta1_se
print("回帰係数の下限値:{}".format(beta1_low))
# 帰無仮説:beta1 = 0 とした場合のt値
t_value1 = beta1/beta1_se
print("t_value:{}".format(t_value1))
stats.model
一生懸命プログラムを作りましたが、実は stats.model というライブラリで全て数行で解決します。
import pandas as pd
import numpy as np
import scipy as sp
from scipy import stats
import statsmodels.formula.api as smf
import statsmodels.api as sm
df = pd.DataFrame({
"x" : [2,3,4,5],
"y" : [6.4,7.9,7.1,8.8],
})
# statsmodel
# 最小二乗法(OLS)による回帰係数の推定
lm_model = smf.ols(formula = "y ~ x", data = df).fit()
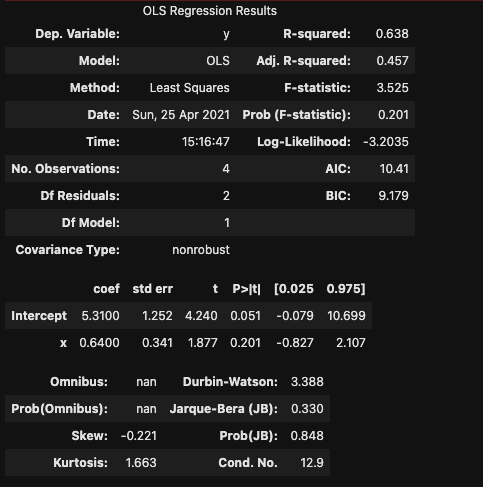
lm_model.summary()
R-squaredが決定係数
Adj.R-squaredが自由度調整済み決定係数
Interceptの行に切片$\beta_0$の推定値・標準誤差・検定の際のt値・p値・下限・上限が並びます。
その下が$\beta_1$のそれぞれです。
重回帰の場合
ちなみにstatsmodelを使うと重回帰の際の回帰係数の推定もすぐ終わります。
$$y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \epsilon_i$$
先程の単回帰モデルよりも一つ説明変数を増やして、説明変数はx1,x2とします。
プログラムではx2の配列ができているところと、formulaの後の書き方が
目的変数 〜 説明変数 となっている部分に説明変数が増えたのでx1+x2となってます。
import pandas as pd
import numpy as np
import scipy as sp
from scipy import stats
import statsmodels.formula.api as smf
import statsmodels.api as sm
df = pd.DataFrame({
"x1" : [2,3,4,5],
"x2" : [1,1,0,1],
"y" : [6.4,7.9,7.1,8.8],
})
# statsmodel
# 最小二乗法(OLS)による回帰係数の推定
lm_model = smf.ols(formula = "y ~ x1+x2", data = df).fit()
lm_model.summary()
satsmodelはRライクな感じで動かせて、Rでも同じ操作感で使えます。