任意の方程式(関数)に対してセカント法(割線法)で1つの解を求めるプログラムを1から書いてみた。
欠陥あるかもしれません。
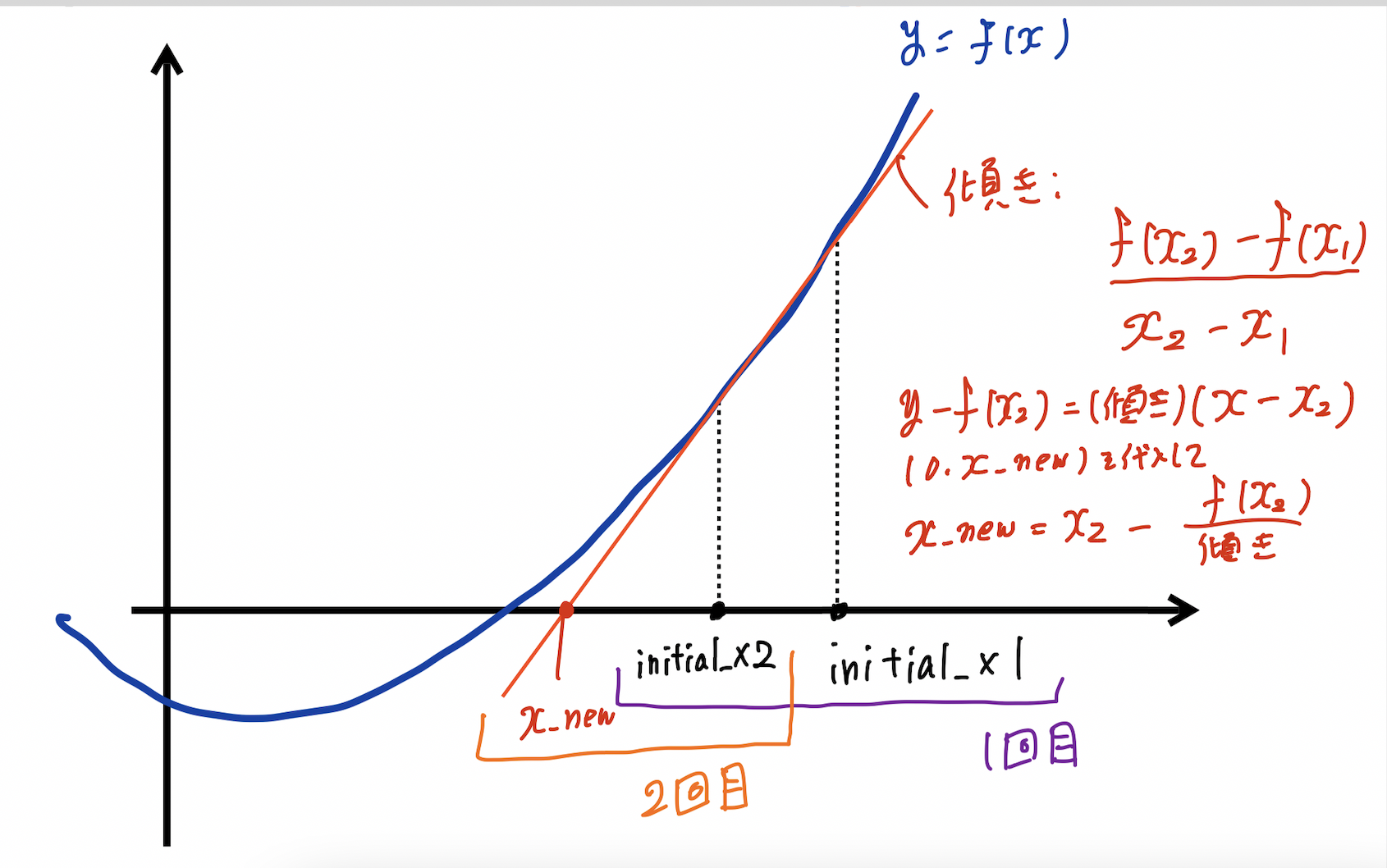
セカント法(割線法)
$$x_{new}=x_{old_2}-\frac{f(x_{old_2})}{\frac{f(x_{old_2})-f(x_{old_1})}{x_{old_2}-x_{old_1}}}$$
基本的にはニュートン法と同じ。
$$x_{new}=x_{old}-\frac{f(x_{old})}{f(x_{old})^{\prime}}$$
$f(x_{old})^{\prime}$が分からない・計算したくない時はセカント法で微分計算を差分近似できる。
セカント法の場合は初期値が2つ必要になる。
設定するもの
・解きたい方程式(関数)
・初期値2つ
・許容誤差
def newton_method(func, initial_x1, initial_x2, r_error):
こういう書き出しで作ってみます。
更新の流れ
$$x_{new}=x_{old_2}-\frac{f(x_{old_2})}{\frac{f(x_{old_2})-f(x_{old_1})}{x_{old_2}-x_{old_1}}}$$
に基づいて、
$|f(x_{初期値1})| >$ 許容誤差
$|f(x_{初期値2})| >$ 許容誤差
ならば更新に入る
$$x_{初期値2}-\frac{f(x_{初期値2})}{\frac{f(x_{初期値2})-f(x_{初期値1})}{x_{初期値2}-x_{初期値1}}}=x_{更新値1}$$
$|f(x_{更新値1})| >$ 許容誤差 ならば
$x_{初期値1}$ の部分を $x_{初期値2}$
$x_{初期値2}$ の部分を $x_{更新値1}$
と改めた上で 次の 更新値2 を求める。
$$x_{更新値1}-\frac{f(x_{更新値1})}{\frac{f(x_{更新値1})-f(x_{初期値2})}{x_{更新値1}-x_{初期値2}}}=x_{更新値2}$$
繰り返していけばそのうち
$|f(x_{更新値n})| <$ 許容誤差 となり許容誤差の範囲に入る。
関数次第では収束しない場合もある。
実装1
# 実装
# 実装
def secant_method(func, initial_x1, initial_x2, r_error):
count = 0
while True:
count += 1
# 初期値1での許容誤差
y_f1 = func(initial_x1)
if abs(y_f1) < r_error:
break
# 初期値2での許容誤差
y_f2 = func(initial_x2)
if abs(y_f2) < r_error:
break
# この2つで許容誤差を満たしていない場合にアルゴリズムに入る
# 更新値を求める
# ニュートン法の微分の部分が差分近似される
y_d = (y_f2-y_f1)/(initial_x2-initial_x1)
x_new = initial_x2 - y_f2/y_d
print("{}回目:x_new = {}".format(count,x_new))
# 更新
initial_x1 = initial_x2
initial_x2 = x_new
関数次第で無限ループします。
実装2で離脱する設定を追加しています。
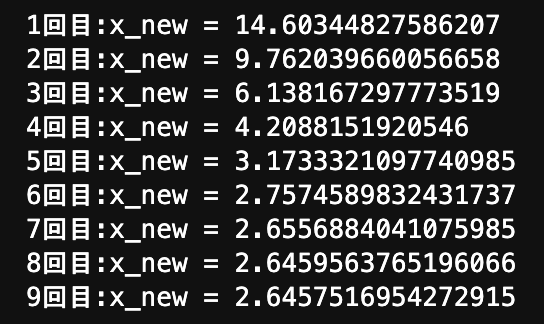
試運転
$\sqrt{7}の近似$
方程式(関数):$x^2-7=0$
初期値は適当に30と28
許容誤差:0.001
# 関数部分はlambda関数で指定する
secant_method(lambda x : x**2 - 7, 30, 28, 0.001)
実装2
・countと誤差の推移のグラフを追加
・100回で収束しない場合の撤退を追加
import matplotlib.pyplot as plt
import numpy as np
# 実装
def secant_method(func, initial_x1, initial_x2, r_error):
"""
funcの部分はlambda関数で設定する。
func = lambda x : x**7 - 7
"""
count = 0
# 折線表示のために誤差結果の保存
y_f_value_list = []
while True:
count += 1
# 初期値1での許容誤差
y_f1 = func(initial_x1)
if abs(y_f1) < r_error:
break
# 初期値2での許容誤差
y_f2 = func(initial_x2)
# この値から誤差リストに計上していく
y_f_value_list.append(abs(y_f2))
if abs(y_f2) < r_error:
break
# この2つで許容誤差を満たしていない場合にアルゴリズムに入る
# 更新値を求める
# ニュートン法の微分の部分が差分近似される
y_d = (y_f2-y_f1)/(initial_x2-initial_x1)
x_new = initial_x2 - y_f2/y_d
print("{}回目:x_new = {}".format(count,x_new))
# 更新
initial_x1 = initial_x2
initial_x2 = x_new
# 100回tiralで収束しない場合、計算を止める
if count == 100:
print("近似解見つからず。")
break
# countと誤差の推移
x = np.arange(1, count+1, 1) # 1 ~ n回
y = np.array(y_f_value_list) # 1 ~ n回の各誤差
plt.plot(x, y)
# 横軸と縦軸のラベルを追加
plt.xlabel('trial')
plt.ylabel('r_error')
# 許容誤差の横線
plt.hlines(r_error, 1, count,color="red",linestyles='dashed')
# 折れ線と許容誤差のボーダーを一括で表示
plt.show()
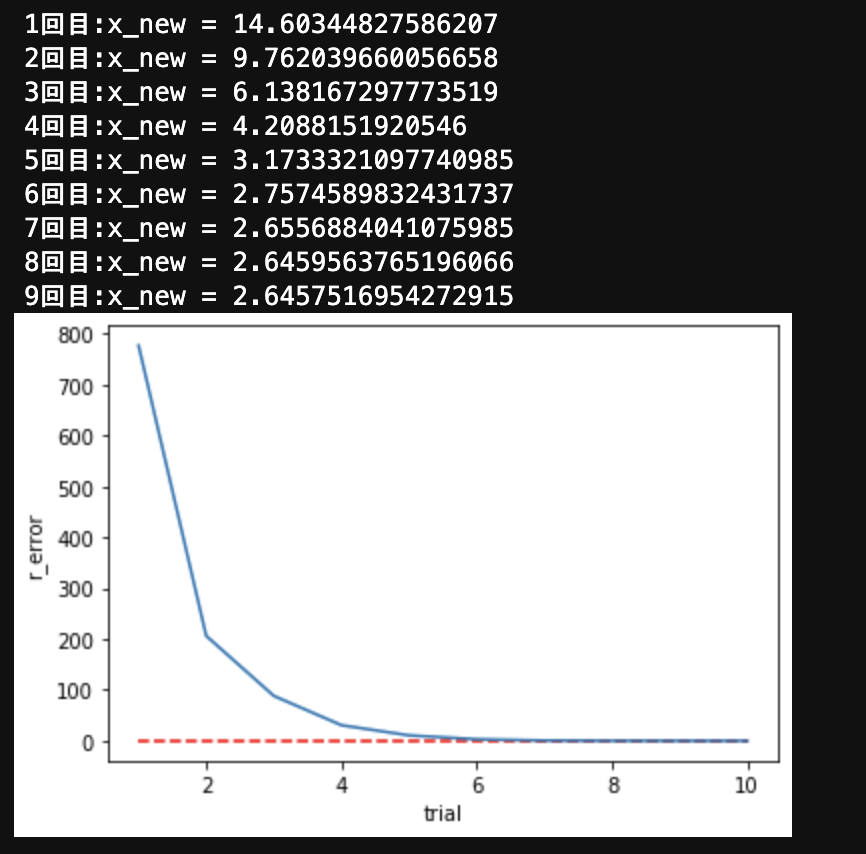
$x^2-7=0$ を初期値30,28から近似する。
secant_method(lambda x : x**2 - 7, 30, 28, 0.001)
実装3
実装1,2は許容誤差を高さに設定して、近似している。
横の動きの更新が浅くなったら近似解にする感じのプログラムも書いてみた。
今回、関数は最初に外に出して定義。
x_ini1:初期値1
x_ini2:初期値2
JJ:繰り返し回数
EPS:許容誤差
$\frac{|x_{new}-x_{old}|}{|x_{old}|} > EPS $
で評価する。
$|x_{new}-x_{old}|$が小さくなればなるほど収束していると考えられる。
値が極端に大きい時にも対応できるように$|x_{old}|$で正規化したものを使った。
def ff(x):
return x**2-7
# 微分の差分近似を返す
def df(x1,x2):
return (ff(x2) - ff(x1)) / (x2-x1)
def secant_method(x_ini1, x_ini2, JJ, EPS):
for i in range(JJ):
x_new = x_ini2 - ff(x_ini2)/df(x_ini1, x_ini2)
if (abs(x_new-x_ini2)/abs(x_ini2)) < EPS:
break
else:
x_ini1 = x_ini2
x_ini2 = x_new
if i == JJ-1:
print("Do not CONVERGE")
else:
return x_new
if (__name__=='__main__'):
JJ = 100
EPS = 0.001
x_ini1 = 30
x_ini2 = 28
x_sol = secant_method(x_ini1, x_ini2, JJ , EPS)
print("solution:{}".format(x_sol))
まとめ
思い出してみると、以前のニュートン法でも微分は中心差分公式を使っていたので、なんか今回のはあまり意味がないかも。
手計算だと微分するかしないかで違いはあるはず。